我们继续来随机看五道AMC8的真题和解析,根据实践经验,对于想了解或者加AMC8美国数学竞赛的孩子来说,吃透AMC8历年真题是备考最科学、最有效的方法之一。
即使不参加AMC8竞赛,吃透了历年真题600道和背后的知识体系,那么小学和初中数学一定会学得非常轻松、游刃有余。(当然,我个人建议孩子有余力的情况下还是参加,以赛促学是一种很不错的做法,能够激发孩子的好胜心和学习热情,也是孩子宝贵的经历、体验。)

为帮助孩子们更高效地备考,我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了原试卷中的少量bug),并且独家制作了多种在线练习,利用碎片化时间,一年足以通过自学在2025年AMC8竞赛中取得好成绩。详情见文末。
好消息,2000-2024年官方发布的高清版真题和答案免费赠送,如有需要的家长和孩子欢迎联系。
2000-2024年AMC8真题和解析:2018年第21题

这道题的考点是数论(余数)。
根据题意,令原来的这个3位数为N,那么N+4就能同时被6,9和11整除,所以N+4是6、9、11的最小公倍数的倍数,很容易得出6、9、11的最小公倍数为198,那么可以假设N+4=198k(假设k是倍数),所以N=198k-4,因为N为一个三位数,所以100≤N=198k-4<1000,即104/198≤k<5又14/198,k=1,2,3,4,5,一共有5个,所以答案为E。
提醒:类似这种题型时常会考到,要从题干中快速找出整除、余数的关系。
2000-2024年AMC8真题和解析:2015年第14题

这道题的考点是数论(倍数)。
假设这4个数分别为n,n+2,n+4,n+6,其中n是奇数。因此这4个数之和为4n+12=4(n+3)。由于n是个奇数,所以n+3是个偶数,则4(n+3)是8的倍数。五个选项中,只有100不是8的倍数,因此,答案为D。
这个解题思路很常见,务必熟练掌握。
2000-2024年AMC8真题和解析:2014年第9题
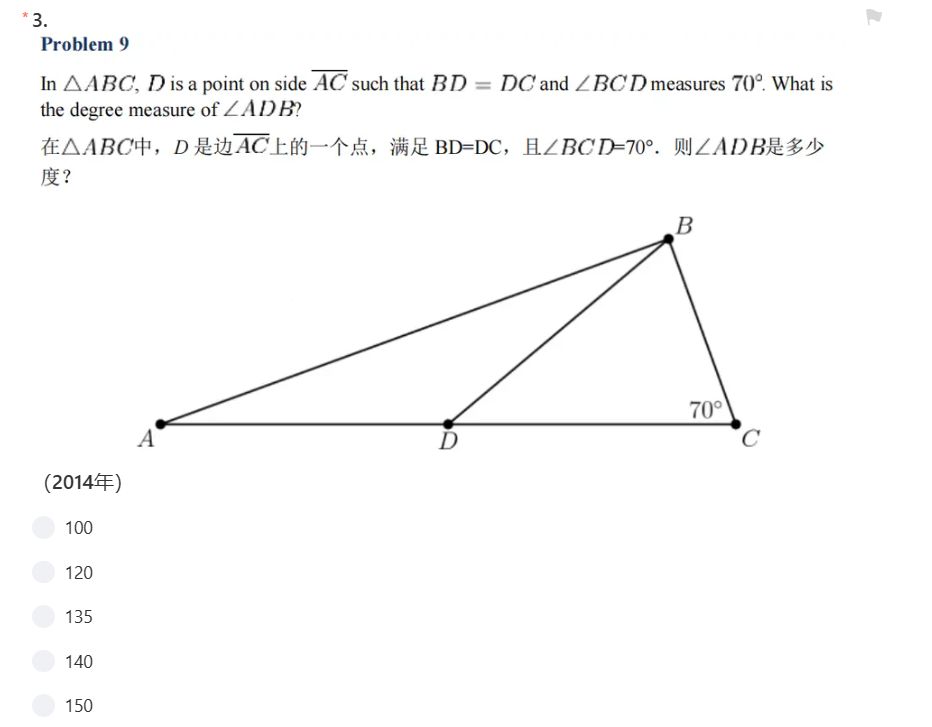
这道题的考点是平面几何(三角形的外角计算)。
因为BD=DC,所以△BDC是等腰三角形,∠DBC=∠DCB=70°,根据根据三角形外角的性质:三角形的外角等于和它不相邻的两个内角的和,可得∠ADB=∠DBC+∠DCB=140°,答案选D。
提醒:几何的一些基本性质和图形要熟练掌握,考试可快速作答。
2000-2024年AMC8真题和解析:2007年第15题

这道题的考点是不等式。
因为c>b,当再加上一个正数,肯定还是大于b,所以A不可能。答案选A。
考试的时候快速选定后即可,作为备考,我们可以再研究一下其他选项,以巩固这方面的知识,训练思维:
- 假设令a=l,b=3,c=l0,则ab<c,且a+b<c,所以B和C都是可能的。
- 假设令a=1/100,b=1,c=2,则a•c<b,D是可能的。
- 假设令a=1/2,b=4,c=8,则b/c=a,E是可能的。
2000-2024年AMC8真题和解析:2005年第6题

这道题的考点是代数(不等式)。
根据题意,2.00d5>2.005,所以d要大于等于5,因为且d只可以取0~9中的数字,因此d=5,6,7,8,9共5个,答案选C。
六分成长针对AMC8备考资源,欢迎了解更多

上述六分成长独家制作的在线练习题,符合学习和认知心理学,来源于完整的历年AMC8真题,并且会持续更新。AMC8备考可用,反复练习,也有利于小学、初中数学能力提升。
还有配套的系统学习文档、视频资料赠送。欢迎了解。