算法题目记录

1.杂题

1.1 计算二进制中1的个数

AcWing

import java.util.*;

public class Main{
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] num = new int[n];
        for (int i = 0; i < n; i++) {
            num[i] = sc.nextInt();
        }
        int[] arr = new int[n];
        int j = 0;
        for (int i : num) {
            if (i == 0) {
                arr[j++] = 0;
                continue;
            }
            int x = 1;
            while ((i & (~i + 1)) != 0) {//每次能取到最右边的1
                i = i ^ i & (~i + 1);
                arr[j] = x++;
            }
            j++;
        }
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
}

1.2 颜色分类

class Solution {
    public void sortColors(int[] nums) {
        int l = -1;//左指针
        int r = nums.length;//右指针
        int i = 0;//哨兵指针
        while (i < r) {
            if (nums[i] < 1) {//左指针下一个数我是看过的，因此i可以++
                 int temp = nums[i];
                nums[i] = nums[l+1];
                nums[l+1] = temp;
                i++;
                l++;              
            }
            else if (nums[i] > 1) {//如果比1大，就和右指针前一个数交换位置。但i不变，因为nums[i]是刚交换过去的，还没比较     
                int temp = nums[i];
                nums[i] = nums[r-1];
                nums[r-1] = temp;
                r--;
            }
            else  {
                i++;
            }
        }
        
    }
}

2.链表

2.1判断是否是回文链表

1.方法一：利用栈反转链表

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
        Stack<ListNode> listNodes = new Stack<>();
        ListNode p = head;
        //利用栈反转链表，判断是否是回文链表
        while (p != null) {//将链表中所有元素入栈
            listNodes.push(p);
            p = p.next;
        }
        while (!listNodes.empty()) {
            if (listNodes.pop().val == head.val) {//
                head = head.next;
            } else {
                return false;
            }
        }
        return true;
    }
}

2.方法2：利用快慢指针

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public boolean isPalindrome(ListNode head) {
    //代表快指针，一次走两步
        ListNode fast = head;
        //代表慢指针，一次走一步
        ListNode slow = head;
        while (fast.next != null && fast.next.next != null) {
            fast = fast.next.next;
            slow = slow.next;
        }
        //退出循环时，如果链表节点是奇数个，快指针在尾节点，慢指针在中点。如果是偶数个，快指针还是在尾节点，慢指针在中点前一个。
        //把右半部分链表反转
        slow = reverseList(slow.next);
        while (slow != null) {
            if (head.val != slow.val) return false;//值不相同，直接返回false
            head = head.next;
            slow = slow.next;
        }
        return true;
    }
    //反转链表
    public static ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode pre = null;
        while (cur != null) {
            ListNode temp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }
}

2.2 模板题：反转链表

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode reverseList(ListNode head) {
        //cur：用于遍历链表元素的指针，代表当前遍历到的节点，初始化当然为head了
        ListNode cur = head;
        //pre：代表当前cur节点，反转后应该指向的节点。因为cur初始在head，反转以后就是尾节点了指向null，所以pre初始化为null
        ListNode pre = null;
        while(cur != null){//当元素还没遍历完的时候
            //在cur指向pre前，用于保存cur.next，防止链表找不到了。
            ListNode temp = cur.next;
            //让当前节点cur，指向pre
            cur.next = pre;
            //让pre变为反转链表的最前面一个节点
            pre = cur;
            //让cur移动到原链表的头节点
            cur = temp;
        }
        // 注意：pre的含义还是反转链表的头节点！
        return pre;
    }
}

复杂度分析：
时间复杂度 O(N)O(N)O(N) ：遍历链表使用线性大小时间。
空间复杂度 O(1)O(1)O(1) ：变量 pre 和 cur 使用常数大小额外空间。

已经是最优的解法了，还有一种递归方法就不赘述了。

2.3 分割链表(将链表分为小于某个值，等于某个值，大于某个值)

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode partition(ListNode head, int x) {
if (head == null || head.next == null) return head;

        //代表小于目标值区域的头和尾
        ListNode h1 = null;
        ListNode t1 = null;
        //代表大于等于目标值的头和尾
        ListNode h2 = null;
        ListNode t2 = null;
        //用于保存head的下一个节点
        //注意：这里最后拼接好了以后，小于区域的头就是整个链表的新的头节点，因此，head可以作为遍历链表的指针。
        ListNode next = head.next;
        while (head != null) {//遍历
            next = head.next;
            head.next = null;
            if (head.val < x) {//如果当前节点的val小于目标值
                if (h1 == null) {//如果当前节点是小于区域的第一个节点
                    h1 = head;
                    t1 = head;
                } else {
                    t1.next = head;
                    t1 = head;
                }
            } else {
                if (h2 == null) {//如果当前节点是大于区域的第一个节点
                    h2 = head;
                    t2 = head;
                } else {//其他情况就把该节点尾插法插入链表中
                    t2.next = head;
                    t2 = head;
                }
            }
            head = next;
        }

        //进行小于区域链表和大于等于区域链表的拼接
        if (h2 == null) {//如果没有大于等于区域
            return h1;
        }
        if (h1 == null) {//如果没有小于区域
            return h2;
        }
        //如果两种区域都有，则让小于区域的尾指针指向大于等于区域的头指针
        t1.next = h2;

        return h1;
    }
}

2.4 随机链表的赋值

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;

    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/

class Solution {
    public Node copyRandomList(Node head) {
        //创建一个map，key为老链表的节点。val为新链表的节点
        HashMap<Node,Node> map = new HashMap<Node,Node>();
        Node cur = head;
        //遍历链表，设置map的key和value
        while(cur != null){
            map.put(cur,new Node(cur.val));
            cur = cur.next;
        }
        cur = head;
        //再次遍历老链表，给新链表设置每一个节点的next和random
        while(cur != null){
            //cur 老链表节点
            //map.get(cur) cur对应的新链表
            map.get(cur).next = map.get(cur.next);//设置新链表的next
            map.get(cur).random = map.get(cur.random);//设置新链表的random
            cur = cur.next;
        }
        return map.get(head);
    }
}

2.5环形链表的判断

方法一：利用HashSet集合。

思路：遍历当前链表，每次遍历判断当前节点是否已经存在于set集合中。如果不存在，则把当前节点放入集合。如果已经存在，说明当前节点就是第一个入环节点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public boolean hasCycle(ListNode head) {
        //创建一个set，用于存放链表中已经遍历了的节点
        HashSet<ListNode> set = new HashSet<>();
        while(head != null){
            //如果当前节点已经存在于set，说明存在环形结构
            if(set.contains(head)) return true;
            set.add(head);
            head = head.next;
        }
        return false;
    }
}

方法二：快慢指针

开始时，快慢指针都在头节点的位置。快指针一次走两步，慢指针一次走一步。

如果没有环结构，快指针一定先走到尾节点。

如果有环结构，快慢指针会在换里相遇。而相遇所要走的卷数不会大于两圈。

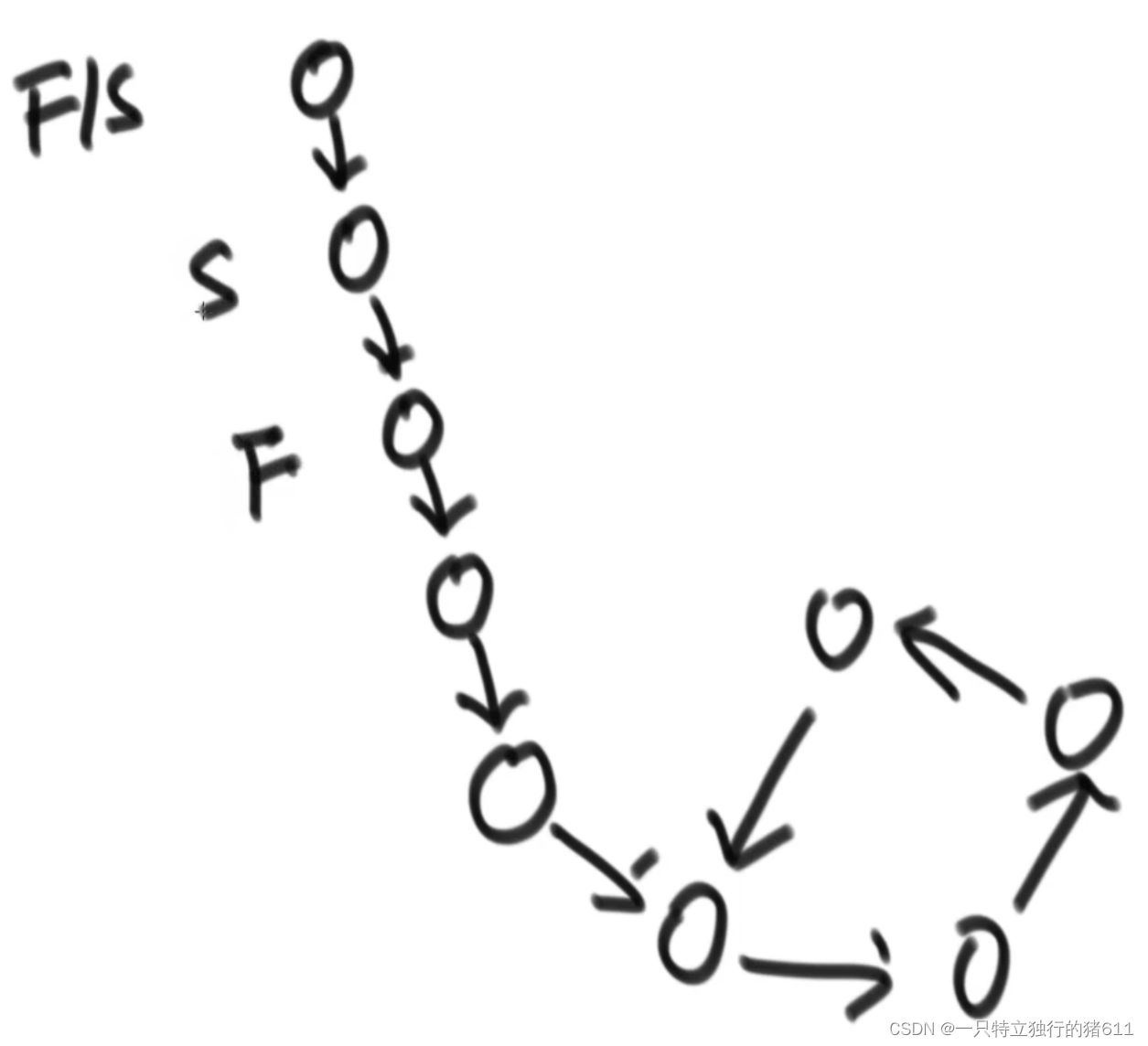
相遇以后，快指针/慢指针到头节点的位置。两个指针开始一次走一步。最终两个指针会在第一次入换节点相遇！(原理就不证明了)

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head == null || head.next == null || head.next.next == null) return null;
        //定义慢指针，一次走一步
        ListNode n1 = head.next;
        //定义快指针，一次走两步
        ListNode n2 = head.next.next;
        while(n1 != n2){//当n1 n2不相遇时循环，所以我开始时没有把两个指针都设置在头节点的位置
            if(n2.next == null || n2.next.next == null){//说明没有环结构，直接返回空
                return null;
            }
            n1 = n1.next;//慢指针一次走一步
            n2 = n2.next.next;//慢指针一次走两步
        }
        //快指针移到头节点，开始一次走一步
        n2 = head;
        while(n1 != n2){//当两个指针相遇时，就走到了第一个入环节点
            n1 = n1.next;
            n2 = n2.next;
        }
        return n1;
    }
}

2.6 链表相交

思路：两个单链表，如何判断有没有相交点呢？

1.先遍历两个链表，到尾节点时停止。如果这时候，两个链表的尾节点都不想等。说明二者不相交。

2.如果二者尾节点是同一个，则计算二者链表长度的差值。让长的链表先走差值个距离。然后，短的链表从头开始走，二者一定会在相交点相遇！

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        //定义两个指针用于遍历两条链表
        ListNode cur1 = headA;
        ListNode cur2 = headB;
        int n = 0;//用于记录两条链表的差值
        while(cur1.next != null){
            cur1 = cur1.next;
            n++;
        }
        while(cur2.next != null){
            cur2 = cur2.next;
            n--;
        }
        if(cur1 != cur2){//尾节点都不想等，说明二者不相交
            return null;
        }
        //这样遍历完两条链表，n就是两条链表的长度差
        cur1 = n > 0 ? headA : headB;//让cur1指向两条链表中长的那一条
        cur2 = cur1 == headA ? headB : headA;//让cur2指向两条链表中短的那一条
        n = Math.abs(n);//n取绝对值
        while(n != 0){//让长的那条链表先移动两条链表差值的距离，再一起走，就会在相交部分汇合！
            cur1 = cur1.next;
            n--;
        }
        while(cur1 != cur2){
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    }
}

3.二叉树

3.1二叉树的最大深度

思路：二叉树的最大深度 = 根节点的最大高度。因此本题可以转换为求二叉树的最大高度。

而求高度的时候应该采用后序遍历。遍历顺序为：左右中。每次遍历的节点按后序遍历顺序，先收集左右孩子的最大高度，再最后处理当前节点的最大高度！因此用后序遍历。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        //注意：这题虽然求的是最大的深度，但我们可以转换思路。求树的最大深度 = 根节点的最大高度！
        if(root == null) return 0;
        //当前节点左孩子的高度
        int leftHeight = maxDepth(root.left);
        //当前节点右孩子的高度
        int rightHeight = maxDepth(root.right);
        return Math.max(leftHeight,rightHeight) + 1;//当前节点的最大高度就是左右孩子中更高的那个+1
    }
}

3.2 搜索二叉树的判断

思路：

首先我们知道二叉搜索树的性质：任何一个节点的左子树的所有节点的值都小于该节点的值，右子树的所有节点的值都大于该节点的值。

由这个性质我们可以知道，对于一个二叉搜索树，中序遍历这个树，得到的结构一定是升序的！

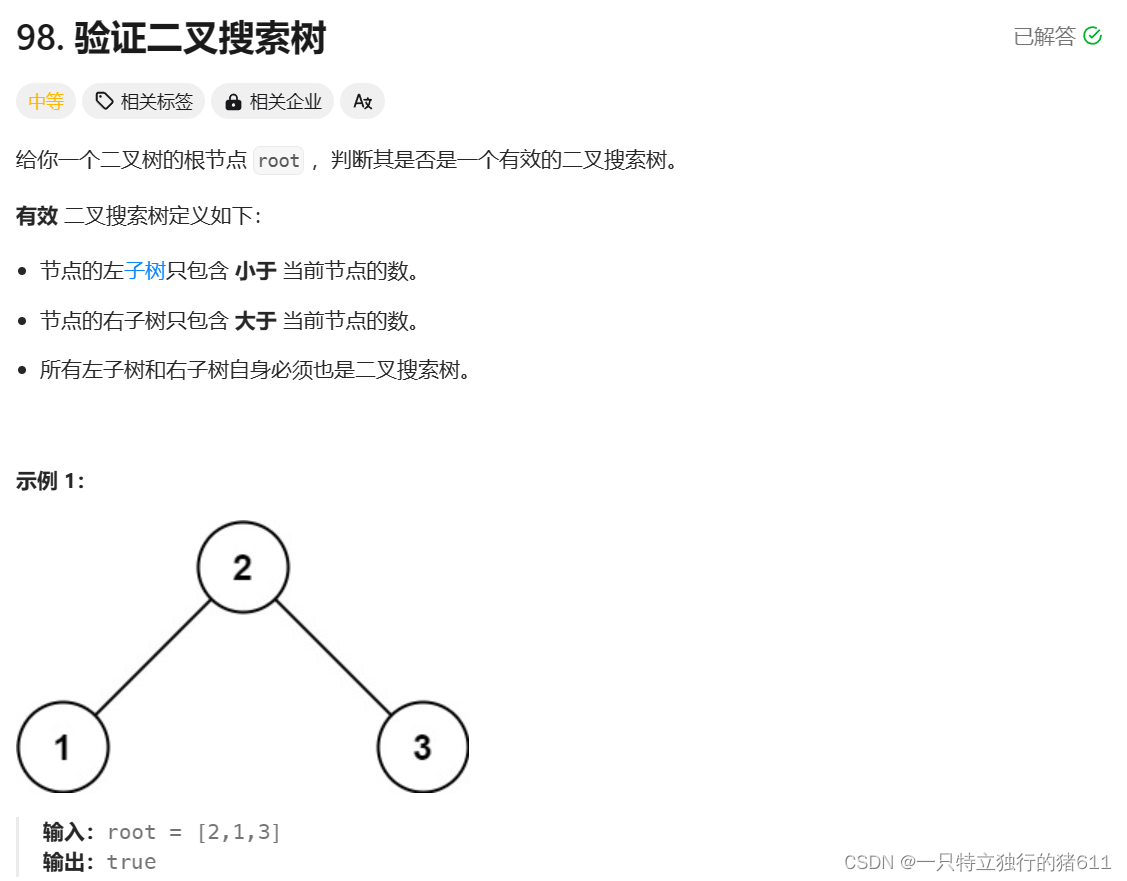
方法一：利用额外的集合，先中序遍历整个树，把每个值取到。再判断集合中是否为升序排序。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public static boolean isValidBST(TreeNode root) {
        if(root.left == null && root.right == null) return true;
        ArrayList<Integer> arr = new ArrayList();//用于存放每个节点值的集合
        f(root,arr);
        for (int i = 0; i < arr.size() - 1; i++) {
            if (arr.get(i + 1) <= arr.get(i)) {
                return false;
            }
        }
        return true;
    }

    public static void f(TreeNode root, ArrayList arr) {//中序遍历
        if (root == null) return;
        f(root.left,arr);
        arr.add(root.val);
        f(root.right,arr);
    }
}

方法二：定义一个变量，用于保存每次要比较值的上一个值的大小。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public static boolean isValidBST(TreeNode root) {
        if (root.left == null && root.right == null) return true;
        Stack<TreeNode> stack = new Stack<>();
        int preValue = Integer.MIN_VALUE;
        while (!stack.isEmpty() || root != null) {
            if (root != null) {//先一路把当前节点的左孩子全部遍历进栈
                stack.push(root);
                root = root.left;
            } else {//总有一个时刻root跑到null，说明当前点没有左孩子
                root = stack.pop();//root赋值为最后一个进栈的没有左孩子的节点

                //这里刚遍历完当前节点的左孩子，如果在这里打印就是中序遍历
                //System.out.print(root.val);
                //所以我们在这里每次比较当前节点，和前一个要比较节点的大小，就相当于中序遍历
                if (root.val > preValue || root.val == Integer.MIN_VALUE) {//说明当前节点满足搜索二叉树的性质
                    preValue = root.val;
                } else {//否则不满足搜索二叉树，直接返回false
                    return false;
                }
                
                root = root.right;//遍历当前节点的右孩子
            }
        }
        return true;
    }
}

3.3 判断完全二叉树

先说下性质：

满二叉树：在一颗二叉树中，如果每个结点都存在左子树和右子树，并且所有叶节点都在同一层上，这样的树为满二叉树。
完全二叉树：相同深度的满二叉树的所有结点（不包含叶子）在该树上都有相应的节点（包含叶子）与之对应且所有左子树先存在，才会存在右子树，然后才会存在下层子树的情况，这样的树为完全二叉树。
可根据下图区分：

思路：层序遍历，根据完全二叉树的性质。

1.当有节点存在有右孩子没左孩子的时候，直接返回false

2.当遍历到第一个叶子节点时，要确保接下来每一个节点都是叶子节点！

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isCompleteTree(TreeNode root) {
         if (root == null) return true;
        //创建一个队列用来做层序遍历
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        TreeNode l = null;//代表当前节点的左孩子
        TreeNode r = null;//代表当前节点的右孩子
        Boolean leaf = false;//一个开关，代表当前有没有遍历到叶子节点
        while (!queue.isEmpty()) {
            root = queue.poll();
            l = root.left;
            r = root.right;
            if (
             (leaf && (l != null || r != null))//前面已经存在叶子节点了，但当前节点不是叶子节点
                            ||
             (l == null && r != null)//有右无左直接返回false
            ) return false;
            if (l == null || r == null) leaf = true;//如果当前节点是叶子节点
            if (l != null) queue.add(l);
            if (r != null) queue.add(r);
        }
        return true;
    }
}

3.4判断平衡二叉树

思路：

根据平衡二叉树的性质，判断当前节点下的树是不是平衡二叉树，只要做到一下几点判断：

1.左孩子要是平衡二叉树

2.右孩子要是平衡二叉树

3.左右孩子的高度差小于等于1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        boolean leftBalanced = isBalanced(root.left);//判断当前节点左子树是不是平衡二叉树
        boolean rightBalanced = isBalanced(root.right);//判断当前节点右子树是不是平衡二叉树
        int leftHeight = getHeight(root.left);//获取左子树高度
        int rightHeight = getHeight(root.right);//获取右子树高度
        //只有当左右子树都为平衡二叉树且左右子树高度差<=1时，当前点才是平衡二叉树
        return leftBalanced && rightBalanced && (Math.abs(leftHeight - rightHeight) <= 1);
    }

    public static int getHeight(TreeNode root) {//获取当前节点的高度
        if (root == null) return 0;
        int leftHeight = getHeight(root.left);//获取当前节点左孩子的高度
        int rightHeight = getHeight(root.right);//获取当前节点右孩子的高度
        return Math.max(leftHeight, rightHeight) + 1;//当前点的高度 = 左右孩子中更高的高度+1
    }
}

3.5找二叉树中两个节点的最近公共祖先

方法一：比较麻烦，空间复杂度较高，但比较好理解。

思路：1.创建一个map集合，先遍历所有节点，把每个节点的父节点存放在当前集合中。

map<当前节点，当前节点的父节点>

2.创建一个set集合，遍历当前节点1的所有祖先节点，并全部放入set集合中。

3.遍历节点2的所有祖先节点。每次遍历判断set集合中有没有当前节点，如果有，当前节点就是二者的共同祖先。由于都是从下网上遍历，所以第一个共同祖先就是最近共同祖先！

注意：这里方法一只提供一种思路，但空间复杂度和时间复杂度都较高，不推荐。

方法一代码：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        HashMap<TreeNode, TreeNode> map = new HashMap<>();
        map.put(root, root);//根节点的父节点就是自己
        f(root, map);
        HashSet<TreeNode> set = new HashSet<>();
        set.add(p);
        TreeNode cur = p;
        while (cur != root) {//从p网上遍历其所有的祖先，把p每一个祖先都存放在set集合中
            set.add(map.get(cur));
            cur = map.get(cur);//当前节点赋值为其父节点
        }
        set.add(root);//根节点单独放入set集合
        cur = q;
        while (cur != root) {//遍历q的所有祖先，把q每个祖先都和p的祖先比较，当出现第一个相同节点，就是二者最近共同的祖先
            if (set.contains(cur)) {
                return cur;
            }
            cur = map.get(cur);//当前节点赋值为其父节点
        }
        return root;
    }
    /**
     * 遍历树，把每个节点的父节点放入map集合中
     *
     * @param root 当前节点
     * @param map  存放节点关系的集合
     */
    public void f(TreeNode root, Map map) {
        if (root == null) {
            return;
        }
       map.put(root.left, root);
        map.put(root.right, root);
        f(root.left, map);
        f(root.right, map);
    }
}

方法二：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        //对于这个方法。如果某个子树下p、q都没有，它一定返回的就是空！

        //遇到空就返回空，遇到p或q就返回p或q
        if(root == null || root == p || root == q) return root;
        TreeNode l = lowestCommonAncestor(root.left,p,q);//当前节点左子树的公共祖先
        TreeNode r = lowestCommonAncestor(root.right,p,q);//当前节点右子树的公共祖先
        if(l != null && r != null) return root;//如果当前节点的左右子树都有p或q。当前节点就是公共祖先
        return l == null ? r : l;//如果左孩子为空就返回右孩子，如果右孩子也是空，那就也返回空！
    }
}

两个节点的分布无非就两种情况：

1.o1、o2中某一个是另一个的祖先。

2.o1、o2两个点分布在某一个公共祖先的两边。

情况一的图：