资源限制
内存限制:256.0MB C/C++时间限制:10.0s Java时间限制:30.0s Python时间限制:50.0s
问题描述
斐波那契串由下列规则生成:
F[0] = "0";
F[1] = "1";
F[n] = F[n-1] + F[n-2] (n≥2,+表示连接)
给出一个由0和1构成的串S和一个数n,求出F[n]中S出现的次数。
输入格式
第一行一个数n。
第二行一个01串S。
输出格式
答案。
样例输入
96
10110101101101
样例输出
7540113804746346428
数据规模和约定
n≤263-1,子串长≤10000,答案≤263-1。
暴力,特别暴力的方法,显然是不行的,但是为了方便理解:(n<=30还是可以的,但这里n很大)
#include<iostream>
#include<string>
using namespace std;
int main(){
long long int n;
string s1="0",s2="1",s3,s;
scanf("%d",&n);
cin>>s;
for(int i=2;i<=n;i++){
s3=s1+s2;
s1=s2;
s2=s3;
}
//求个数
long long int cnt=0;
for(int j=0;j<s3.length();j++){
if(s3.substr(j,s.length())==s){
cnt++;
}
}
printf("%lld\n",cnt);
return 0;
} 以下是100分的代码:
#include<iostream>
#include<string>
using namespace std;
int flag;
long long int L1,L2,L;//成斐波那契数列的答案,L1为第一个不为0的个数,L2为第2个不为0的个数
long long int x;//第一个不为0的位置
int main(){
long long int n;
string s1="0",s2="1",s3,s;
scanf("%lld",&n);
cin>>s;
for(int i=2;i<=n;i++){
s3=s1+s2;
s1=s2;
s2=s3;
for(int j=0;j<s3.length();j++){
if(s3.substr(j,s.length())==s){
flag=1;
break;
}
}
if(flag==1){
x=i;
break;
}
}
for(int j=0;j<s3.length();j++){
if(s3.substr(j,s.length())==s){
L1++;
}
}
s3=s1+s2;
s1=s2;
s2=s3;
for(int j=0;j<s3.length();j++){
if(s3.substr(j,s.length())==s){
L2++;
}
}
for(int i=x+2;i<=n;i++){
L=L1+L2+1;//规律
L1=L2;
L2=L;
}
printf("%lld\n",L);
return 0;
}  思路:s串的个数成类似于斐波那契数列的规律。
思路:s串的个数成类似于斐波那契数列的规律。
虽然前面提到的暴力方法不能求解n很大的情况,但是前25个绝对没问题,根据暴力方法输出前25个来找规律:
假设串s="10110101101101"
#include<iostream>
#include<string>
using namespace std;
int main(){
string s1="0",s2="1",s3,s;
int n;
scanf("%d",&n);
cin>>s;
for(int i=2;i<=n;i++){
s3=s1+s2;
//求个数
int cnt=0;
for(int j=0;j<s3.length();j++){
if(s3.substr(j,s.length())==s){
cnt++;
}
}
printf("n=%d:%d个\n",i,cnt);
s1=s2;
s2=s3;
}
return 0;
} 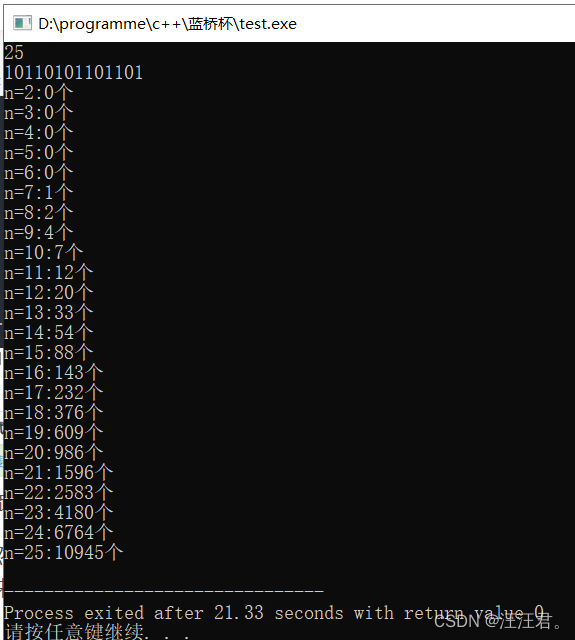
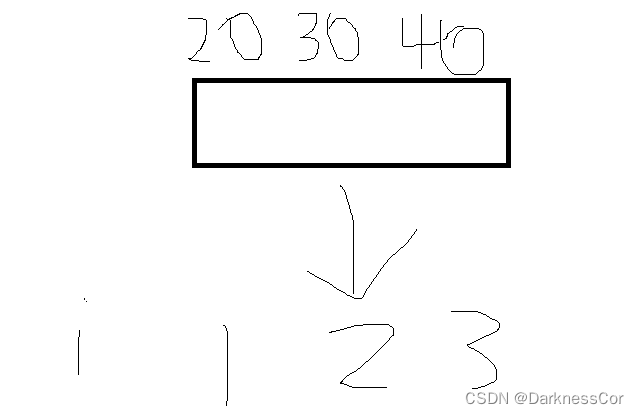
可以发现,从含有串s个数不为0的F[n]之后,如F[7],F[8]之后,有以下规律:
因此只需找到第一个含s串的位置x,求出个数L1,然后求出位置x+1的个数L2,之后根据规律即可求出所有。
//但是这个规律好像也不大对,当s=“01”时:
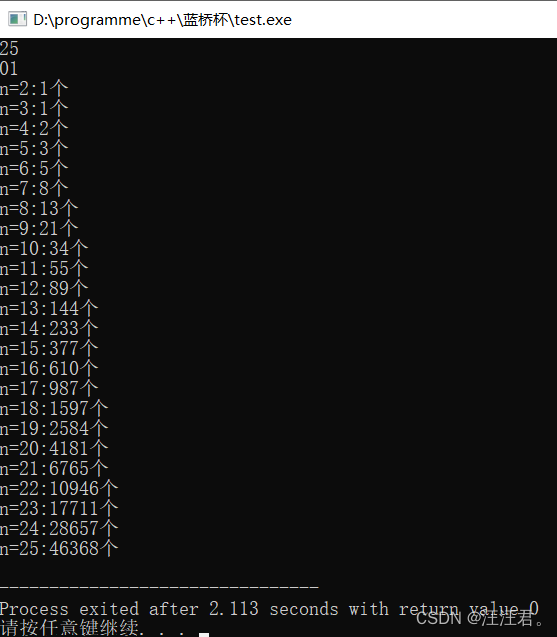
第三个数是前两个数的和,不需要+1了。。这个方法还是不太严谨,虽然它通过了吧。希望可以给你带来一些思路,如果有更好的方法欢迎在评论区留言或私信我。