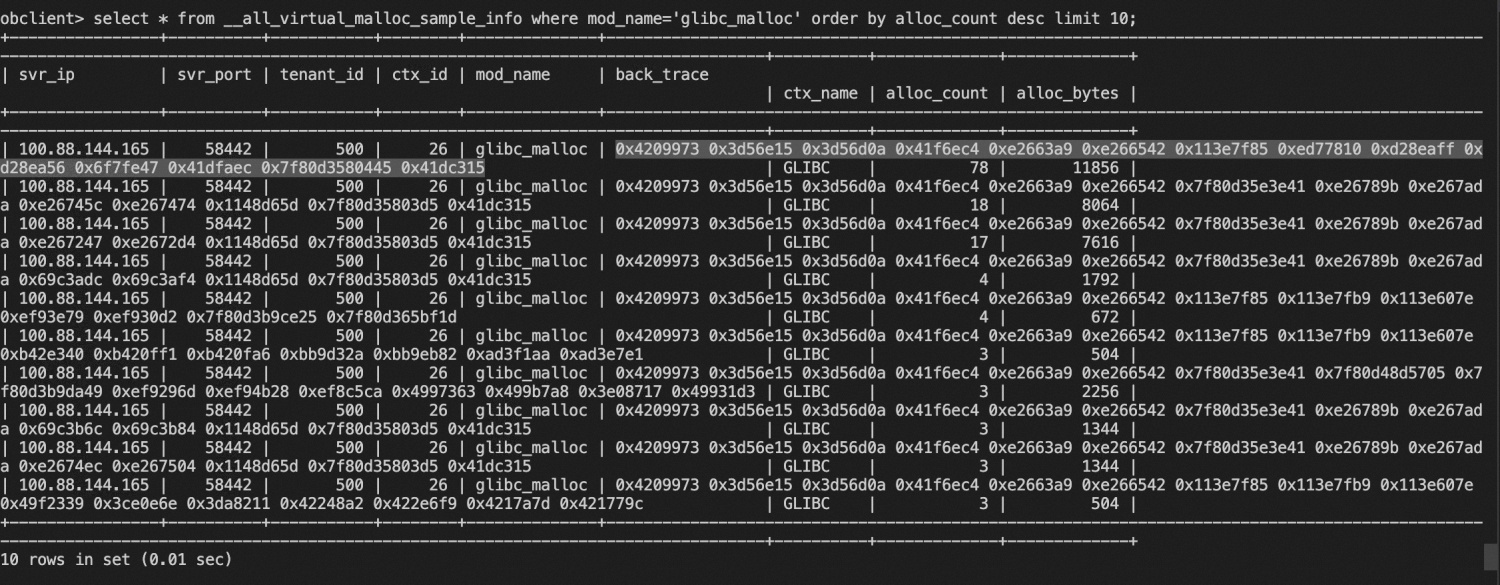
一、题目

凑算式

     B      DEF
A + --- + ------- = 10
     C      GHI

     
  
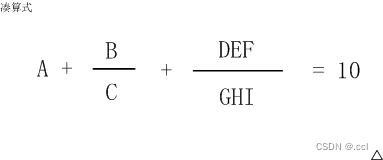
这个算式中A~I代表1~9的数字，不同的字母代表不同的数字。

比如：
6+8/3+952/714 就是一种解法，
5+3/1+972/486 是另一种解法。

这个算式一共有多少种解法？

注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。

二、代码

---

package Lan2016;

public class C凑算式 {
    /*凑算式
    这个算式中A~I代表1~9的数字，不同的字母代表不同的数字。

      B   DEF
   A+---+-----=10
      C   GHI
    比如：
            6+8/3+952/714 就是一种解法，
            5+3/1+972/486 是另一种解法。
    这个算式一共有多少种解法？
    注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。*/
    /*
     * 大致思路：
     * 采用暴力的方法，A遍历1~9，B也遍历1~9，且B与A不能相同，
     * */
    //public static void main(String[] args) {
        /*int count  = 0;
        for (int x1 = 1; x1 < 10; x1++) {
            for (int x2 = 1; x2 < 10; x2++) {
                if (x2 == x1) continue;

                for (int x3 = 1; x3 < 10; x3++) {
                    if (x3 == x1 || x3 == x2) continue;

                    for (int x4 = 1; x4 < 10; x4++) {
                        if (x4 == x3 || x4 == x2 || x4 == x1) continue;

                        for (int x5 = 1; x5 < 10; x5++) {
                            if (x5 == x4 || x5 == x3 || x5 == x2 || x5 == x1) continue;

                            for (int x6 = 1; x6 < 10; x6++) {
                                if (x6 == x5 || x6 == x4 || x6 == x3 || x6 == x2 || x6 == x1) continue;

                                for (int x7 = 1; x7 < 10; x7++) {
                                    if (x7 == x6 || x7 == x5  || x7 == x4 || x7 == x3 || x7 == x2 || x7 == x1)
                                        continue;

                                    for (int x8 = 1; x8 < 10; x8++) {
                                        if (x8 == x7 || x8 == x6 || x8 == x5 || x8 == x4 || x8 == x3 || x8 == x2 || x8 == x1)
                                            continue;

                                        for (int x9 = 1; x9 < 10; x9++) {
                                            if (x9 == x8 || x9 == x7 || x9 == x6 || x9 == x5 || x9 == x4 || x9 == x3 || x9 == x2 || x9 == x1)
                                                continue;
                                            if (x1 + (x2 / x3) + ((x4 * 100 + x5 * 10 + x6) / (x7 * 100 + x8 * 10 + x9)) == 10) {
*//*
                                                System.out.println(x1 +" "+x2 + " " + x3 + " " + x4 +" "+ x5 +" " + x6 + " " +x7 +" "+ x8 + " "+x9);
*//*
                                                count++;
                                            }
                                        }
                                    }
                                }
                            }
                        }
                    }
                }
            }

        }
        System.out.println(count);*/
    /*
     * 参考答案：
     * 需要用到深度优先遍历
     * */

    //主函数里面需要 调用深度优先的算法 并输出结果值
    public static void main(String[] args) {
        dfs(0);
        System.out.println(count);
    }

    //定义一个数组用来存1~9这9个数
    static int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9};
    static int count = 0;

    //定义深度优先的算法
    private static void dfs(int m) {


        //当输入进来的数字的个数大于等于9的时候,我们才判断看是否是满足条件的数
        if (m >= 9) {
            int x1 = arr[0];
            int x2 = arr[1];
            int x3 = arr[2];
            int x4 = (100 * arr[3] + 10 * arr[4] + arr[5]);
            int x5 = (100 * arr[6] + 10 * arr[7] + arr[8]);
            //如果按照下面这个式子来判断的话，会有小数的出现，而我们定义的是Int类型的，
        /*   x2   x4
          x1+---+-----=10
             x3   x5*/
            //所以把它转化成整数的形式，x1*x3*x5 + x2*x5 + x4 * x3 = 10*x3*x5
            if (x1 * x3 * x5 + x2 * x5 + x4 * x3 == 10 * x3 * x5) {
                //当满足条件的时候，我们计数器加一，
                count++;
                //输出数组中的数
                for (int i = 0; i < 9; i++) {
                    System.out.print(arr[i] + " ");
                }
                System.out.println();//换行
            }
            return;
        }

        //深度优先搜索
        for (int i = m; i < 9; i++) {
            //交换m和i的值
            swap(m, i);
            dfs(m+1);
            swap(m,i);
        }
    }

    //swap函数
    static void swap(int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

三、反思

        1.解题思路：我们要解决的问题就是 看哪些数字符合题目中的算式，我们需要找出所有可能的数字组合，将符合条件的加入到我们的计数器，

        2.我们将这些数字放到数组里面，方面我们可以进行数字的交换，方便遍历、访问、排序和搜索等，

        3.定义数组和计数器的时候，我们定义成static静态的，确保整个类都能访问，例如main中访问的count，dfs中访问的arr数组和count

        4.我们的深度优先算法的核心：

for (int i = m; i < 9; i++) {
            //交换m和i的值
            swap(m, i);
            dfs(m+1);
            swap(m,i);
        }

通过不断的交换、递归、回溯，来遍历到所有的可能，交换下标为m和i的值，从而有新的排列组合，递归调用dfs,传入m+1，来找下一个位置的排列组合。

        5.输出：29

有问题欢迎大家来提