【算法】一类支持向量机OC-SVM
- 前言
- 一类支持向量机OC-SVM 概念介绍
- 示例编写
- 数据集创建
- 实现一类支持向量机OC-SVM
- 完整的示例输出
前言
由于之前毕设期间主要的工具就是支持向量机,从基础的回归和分类到后来的优化,在接触到支持向量机还有一类支持向量机的,对其产生了一定的兴趣,并对研究过程中的相关示例进行记录,主要是基础的一类支持向量机OC-SVM示例和蜂群算法优化一类支持向量机超参数示例,方便后续的查看。
一类支持向量机OC-SVM 概念介绍
OC-SVM(One-Class Support Vector Machine)是一种支持向量机(Support Vector Machine,SVM)的变体,用于异常检测和异常检测问题。与传统的SVM只能处理二分类问题不同,OC-SVM旨在通过仅使用正例样本来学习一个描述正例样本特征的超平面,并尽可能将负例样本远离该超平面。
在OC-SVM中,训练样本仅包含正例样本,目标是找到一个最优的超平面,使得正例样本尽可能地位于该超平面上方,并使负例样本尽可能地位于该超平面下方。这样,当新的样本点被映射到特征空间时,可以根据其相对于超平面的位置进行分类,从而判断其是否为异常样本。
该介绍不那么通俗易懂,看了一篇文章,简单的说,以前的svm 分类有明细的划分,现在的oc-svm则只有一个类别的划分,也就是正例,至于其他的都归属于负例。这个在大神的知乎文章什么是一类支持向量机(one class SVM),是指分两类的支持向量机吗?中有通俗的例子讲解,这边不进行重复论述。
示例编写
主要是基于vscode 编译器展开python的编写,只需要在扩展中下载Python 插件即可。
数据集创建
数据集包括测试与训练集,由于一类支持向量机OC-SVM在示例中只要采用python 中的OneClassSVM,而它返回的预测标签如果 正常数据点返回 1,异常点返回 -1 ,因此在数据集的标签要做相应的处理,正例为1,负例为-1。
# 假设 X 是训练数据,它应该是一个形状为 (n_samples, n_features) 的二维数组
# 这里我们创建一个简单的示例数据集
X = np.random.normal(size=(100, 2))
binary_array = np.random.randint(2, size=100)
binary_array=np.where(binary_array == 0, -1, 1)
# 预测
# 使用训练好的模型预测新数据点的标签,正常数据点返回 1,异常点返回 -1
X_test = np.random.normal(size=(10, 2))
实现一类支持向量机OC-SVM
主要采用OneClassSVM,也是sklearn库里面的,pip 一下就行。使用起来跟svm 基本一样。
# 创建一个 OneClassSVM 对象
# 通过 'nu' 参数来控制错误率的上界和支持向量的比例
# 'kernel' 参数可以选择核函数,例如 'rbf' 代表径向基函数核
# 'gamma' 是 'rbf', 'poly' 和 'sigmoid' 核函数的系数
ocsvm = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
- ‘nu’ 参数来控制错误率的上界和支持向量的比例
- ‘kernel’ 参数可以选择核函数,例如 ‘rbf’ 代表径向基函数核
- ‘gamma’ 是 ‘rbf’, ‘poly’ 和 ‘sigmoid’ 核函数的系数
- ‘shrinking’ 参数如果设为 True,则会使用启发式收缩
- ‘tol’ 是停止训练的误差值大小
- ‘cache_size’ 是指定训练时使用的缓存大小
- ‘verbose’ 是控制日志输出的数量
这个可以直接看源码的注释,里面都有介绍。
完整的示例输出
# demo
from sklearn import svm
import numpy as np
# 假设 X 是训练数据,它应该是一个形状为 (n_samples, n_features) 的二维数组
# 这里我们创建一个简单的示例数据集
X = np.random.normal(size=(100, 2))
binary_array = np.random.randint(2, size=100)
binary_array=np.where(binary_array == 0, -1, 1)
print(binary_array)
# 创建一个 OneClassSVM 对象
# 通过 'nu' 参数来控制错误率的上界和支持向量的比例
# 'kernel' 参数可以选择核函数,例如 'rbf' 代表径向基函数核
# 'gamma' 是 'rbf', 'poly' 和 'sigmoid' 核函数的系数
ocsvm = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
# 训练模型
ocsvm.fit(X,binary_array)
# 预测
# 使用训练好的模型预测新数据点的标签,正常数据点返回 1,异常点返回 -1
X_test = np.random.normal(size=(10, 2))
# print(X_test)
print("--------------")
predictions = ocsvm.predict(X_test)
# 输出预测结果
print(predictions)
print("--------------")
# 也可以使用 decision_function 方法来获取每个样本到决策边界的距离
# 负数通常表示异常值
distances = ocsvm.decision_function(X_test)
print(distances)
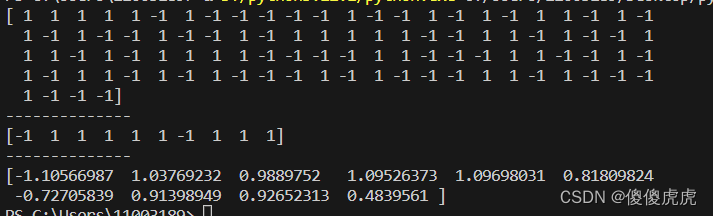
从输出的结果来看,有2组示例预测为负例,然后可以通过与真实标签比较,调整超参数来提交预测的精度。也可以嵌入寻优方法,这个在往期博文都有介绍,比如ga、pso等等。
在资源中上传了用蜂群算法优化一类支持向量机超参数的2个示例,有需要可以直接下载使用。