思路： 之前做过普通二叉树求共工作祖先的问题，有两种情况，

• 第一种是：如果一个节点的左孩子和右孩子分别包含p，q节点，那么这个节点是p和q的最近公共祖先。
• 第二种是：当前节点是p或q，其孩子节点包含q或p，则返回当前节点。
  那么本题是二叉搜索树，可以根据val的大小选择继续递归的方向是向左还是向右。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null) return null;
        if(p.val<root.val && q.val<root.val) return lowestCommonAncestor(root.left,p,q);
        if(p.val>root.val && q.val>root.val) return lowestCommonAncestor(root.right,p,q);
        return root;
    }

}

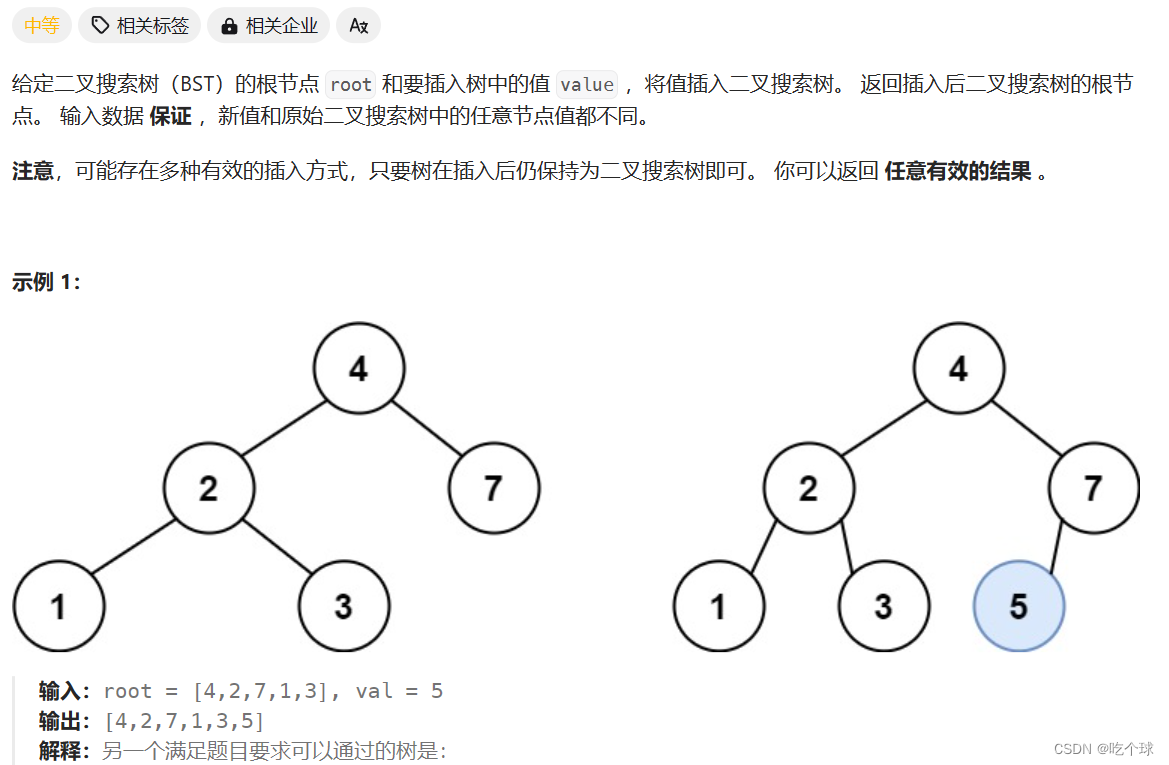
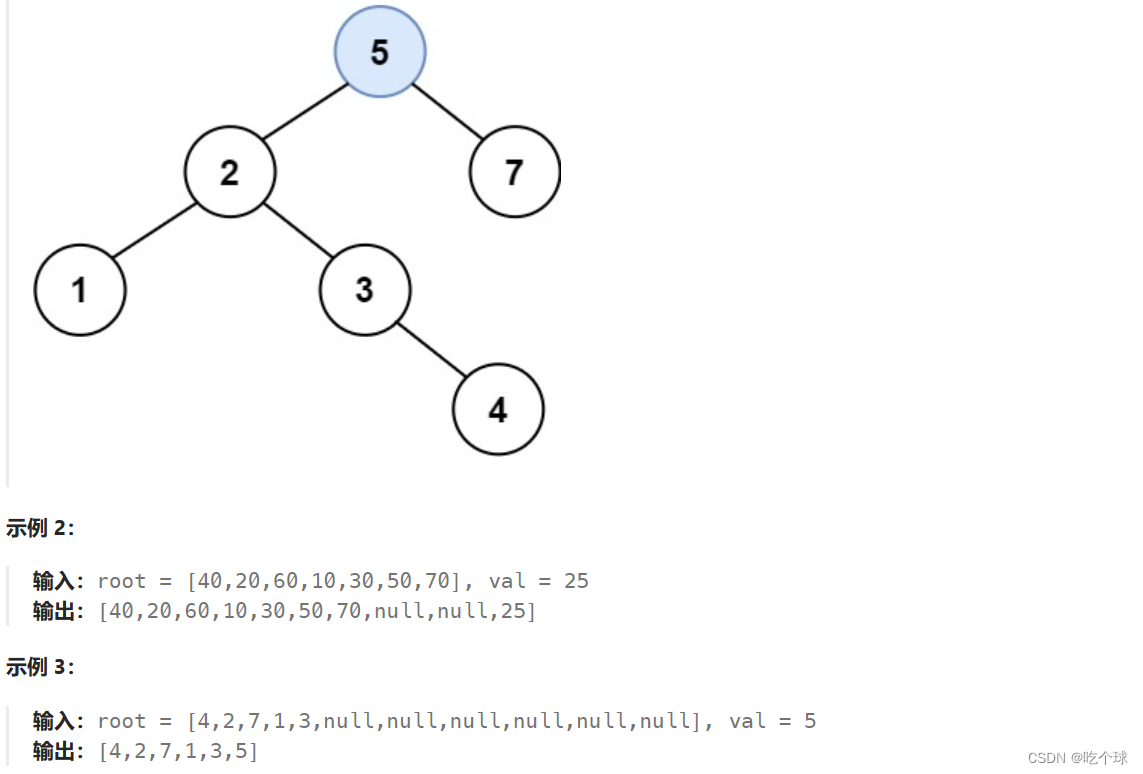
思路： 可以不考虑题目中提示所说的改变树的结构的插入方式。一定存在一个叶子节点，使val值作为它的左或右孩子是合理的。
可以不考虑题目中提示所说的改变树的结构的插入方式。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        return delete(root,key);
    }

    public TreeNode delete(TreeNode node,int key){
        if(node==null) return null;
        if(node.val==key){
            if(node.left==null && node.right==null) return null;
            else if(node.left!=null && node.right==null) return node.left;
            else if(node.left==null && node.right!=null) return node.right;
            else{
                TreeNode cur=node.right;
                while(cur.left!=null) cur=cur.left;
                cur.left=node.left;
                return node.right;
            }
        }
        if(key<node.val){
            node.left=delete(node.left,key);
        }
        else{
            node.right=delete(node.right,key);
        }
        return node;
    }
}

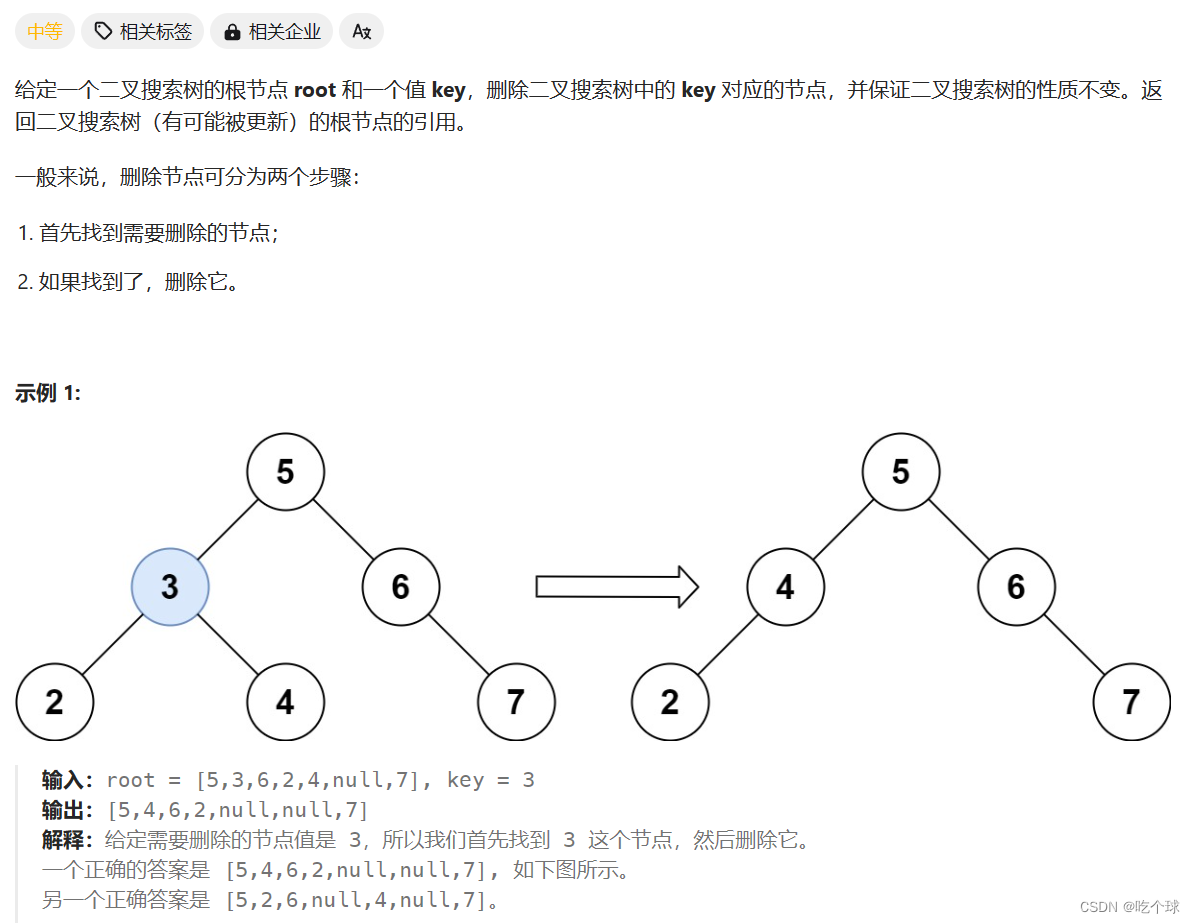
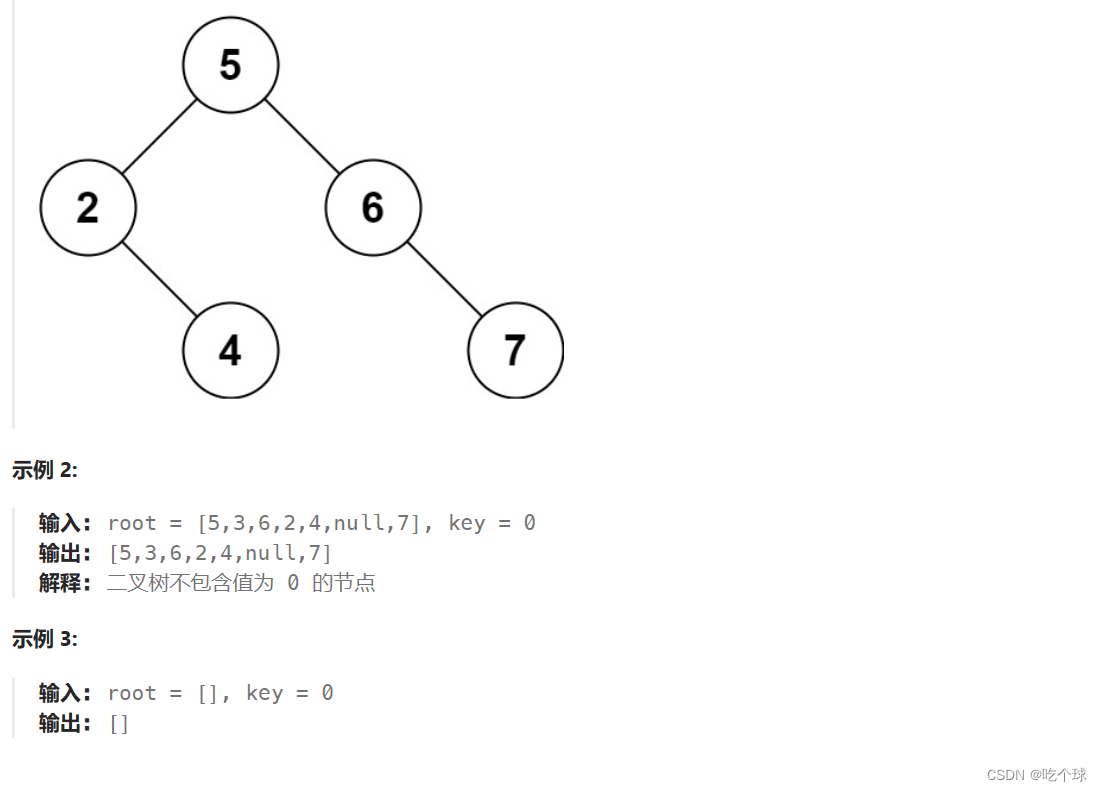
思路： 相对于上一题的插入操作，本题就有难度了，涉及到改树的结构 。
要充分考虑到五种情况：

没有找到删除的节点

• 第一种情况：没找到删除的节点，遍历到空节点直接返回了

找到删除的节点

• 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点
• 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
• 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
• 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。
  第五种情况有点难以理解，看下面动画：
  

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        return delete(root,key);
    }

    public TreeNode delete(TreeNode node,int key){
        if(node==null) return null;
        if(node.val==key){
            if(node.left==null && node.right==null) return null;
            else if(node.left!=null && node.right==null) return node.left;
            else if(node.left==null && node.right!=null) return node.right;
            else{
                TreeNode cur=node.right;
                while(cur.left!=null) cur=cur.left;
                cur.left=node.left;
                return node.right;
            }
        }
        if(key<node.val){
            node.left=delete(node.left,key);
        }
        else{
            node.right=delete(node.right,key);
        }
        return node;
    }
}