前言:
本篇主要参考《Wasserstein GAN and the Kantorovich-Rubinstein Duality》
重点介绍一下 WGAN 的损失函数 是如何通过 Wasserstein Distance 变换过来的。
分为5步:
- 我们首先建立Wasserstein Distance 极小值形式,
- 经过对偶变换得到Wasserstein Distance 极大值形式,
- 通过Farkas 引理证明其二者是强对偶关系,
- 利用对偶形式的约束函数 对 极大值形式 进行变换,得到WGAN 损失函数形式
- 极大值的约束函数就是1-Lipschitz
目录:
- Earth Mover’s Distance
- 对偶形式(Dual Form)
- Farkas 引理(Farkas Theorem)
- 强对偶(Strong Duality)
- 传输成本的对偶( Dual Implementation)
- 对偶到WGAN
- Lipschitz约束和Wasserstein 关系
一 Earth Mover’s Distance
我们以任意两个离散的概率分布 为例
1.1 EMD 距离定义
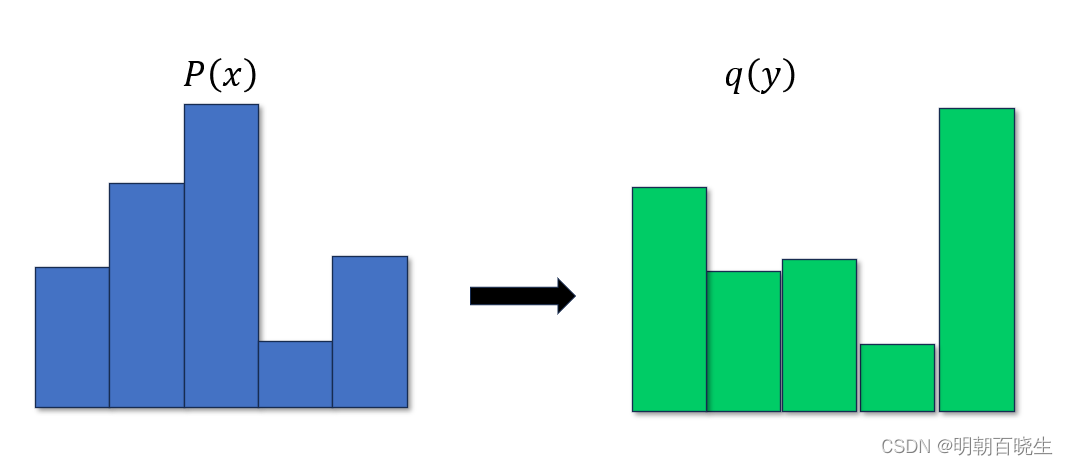
一种用来测量两个概率分布之间的距离度量。它主要应用在图像处理和语音信号处理领域。EMD问题可以通过线性规划来求解,其核心思想是将一个分布的密度通过“搬土”的方式转移到另一个分布的位置上,使得转移的代价最小。在这个过程中,每个点对之间的距离和转移的量共同决定了总的工作量,即EMD
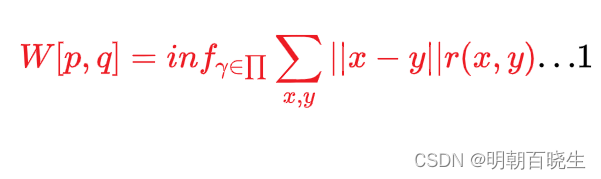
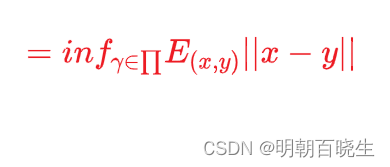
优化的目标:
求解,使得
达到极小值
其中:
:离散的随机分布,对应状态变量
的维度为
(图像中就是对应每个像素值变化范围0-255)
离散的随机分布,对应状态变量
的维度为
: 代表推土方案,是
的联合概率分布函数
: 积分下限 ,等价于求极小值
约束条件
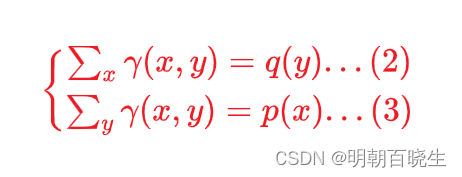
1. 2 矩阵表达形式
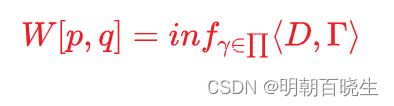
is Frobenius inner product: 两个大小相同的矩阵元素一一对应相乘并且相加
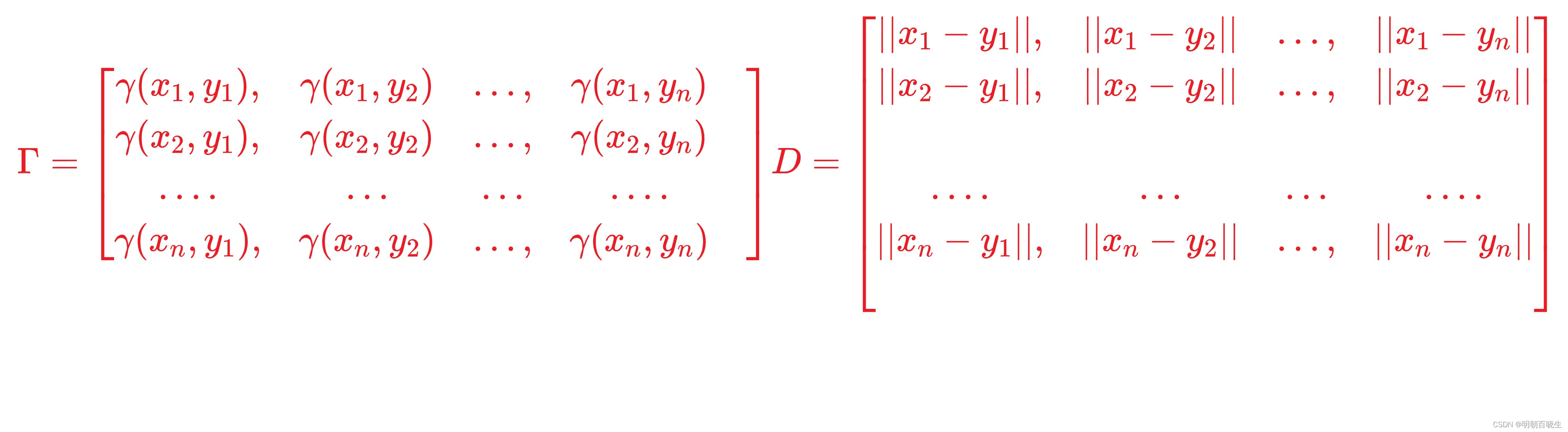
1.3 EMD 向量表达形式
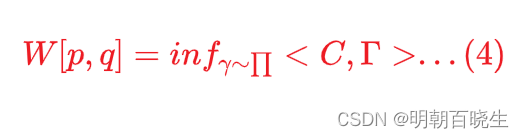
通过求解optimal transport plan , 使得EMD 最小

约束条件:
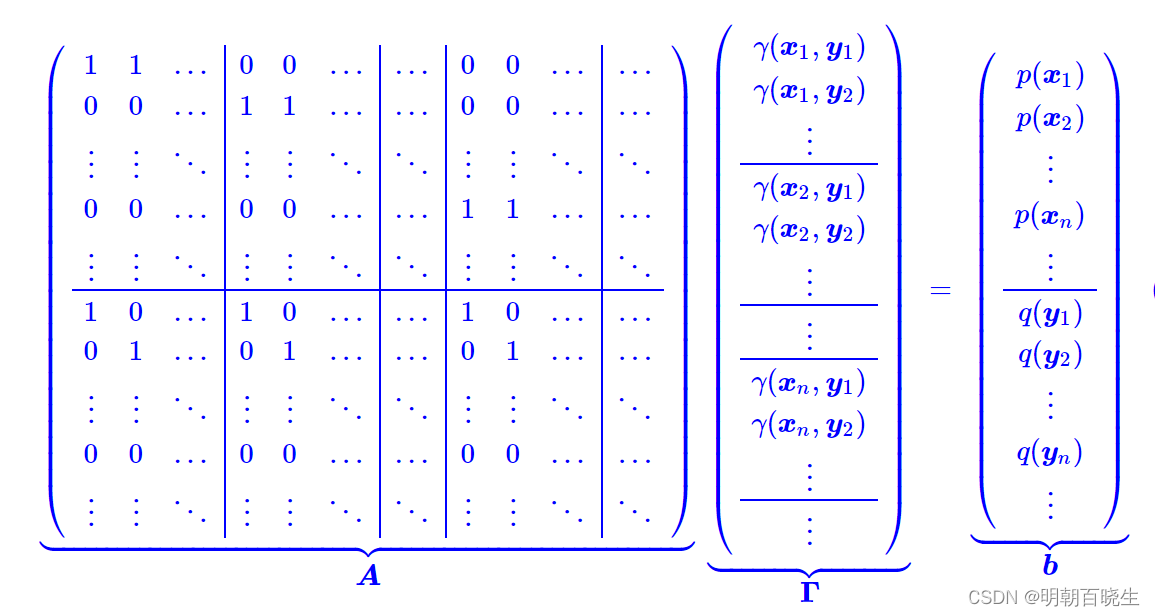
1.4 线性规划问题(LP: Linear Programming)
通过上面我们可以看到EMD等价于LP问题:
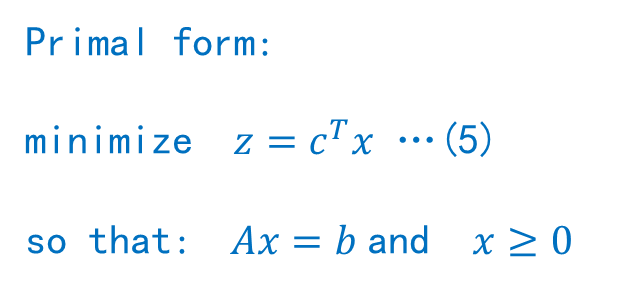
Python 有对应的LP 库,如下例子
# -*- coding: utf-8 -*-
"""
Created on Sun Mar 10 20:58:19 2024
@author: cxf
"""
import numpy as np
from scipy.optimize import linprog
def run():
"""
数学规划模型
scppy.optimize.linprog
"""
c=np.array([-2,-3,5]).transpose() #行列向量不影响求解
A=np.array([[-2,5,-1],[1,3,1]])
b=np.array([-10,12])
Aeq=np.array([[1,1,1]]) # 单个约束也要表示为矩阵形式
beq=np.array([7])
x=linprog(c,A,b,Aeq,beq,method='highs',bounds=np.array([[0,None],[0,None],[0,None]]))
print(x)
def main():
'''
LINPROG_METHODS = ['simplex',
'revised simplex',
'interior-point',
'highs',
'highs-ds',
'highs-ipm']
Returns
-------
None.
'''
print("\n ------1--------")
P_r = np.array([[0.1,0.9]]).transpose()
P_t = np.array([[0.5,0.5]]).transpose()
D = np.array([[0.0,1.0],
[1.0,0.0]])
L,L = D.shape
C = D.reshape((L**2,1))
print("\n C: distance |x-y| 功能 \n",C)
A_r = np.zeros((L,L,L))
A_t = np.zeros((L,L,L))
for i in range(L):
for j in range(L):
A_r[i,i,j]=1
A_t[i,j,i]=1
#Aeq是约束条件
aeq = np.concatenate((A_r.reshape(L,L**2),A_t.reshape(L,L**2)),axis=0)
print("\n 约束条件:Ax=b: \n",aeq,aeq.shape)
#b 就是Pr,Pg 的概率分布组成一列
beq = np.concatenate((P_r,P_t),axis=0)
print("\n vec(pr,pg) :\n",beq)
bound = np.repeat([[0.0,1.0]],L*L,axis=0)
print("\n 0=<x<1 \n",bound)
#x[L*L,1]
#bounds=bound
opt_res= linprog(C,A_eq=aeq, b_eq=beq, method='highs-ds',bounds=bound)
emd = opt_res.fun
#gamma = opt_res.x.reshape((1,1))
print("\n x:\n ",opt_res.x)
print("\n-----------")
main()二 对偶形式(Dual Form)
原始形式 问题:
不幸的是,这种优化在很多情况下并不实用,尤其是在通常使用 GAN 的领域。在我们的示例中,我们使用具有十种可能状态的一维随机变量。可能的离散状态的数量随着输入变量的维度数量呈指数级增长。对于许多应用,例如图像,输入很容易就有数千个维度。即使是近似值那么几乎是不可能的。 但实际上我们并不关心。我们只想要一个数字,即 EMD。此外,我们想用它来训练我们的生成器网络,该网络生成分布,为此,我们必须能够计算梯度。自从p和q只是我们优化的限制,这不可能以任何直接的方式实现. 事实证明,还有另一种更方便的 EMD 计算方法。任何 LP 有两种方式可以表述问题:我们刚才使用的原始形式和对偶形式。

证明:
设
因为
是标量,所以
这种形式也称为弱对偶形式,那是否有强对偶使得
三 Farkas 引理
强对偶形式的证明,主要用到称之为“Farkas 引理”的结论:
对 , 以下两个命题是互斥的:
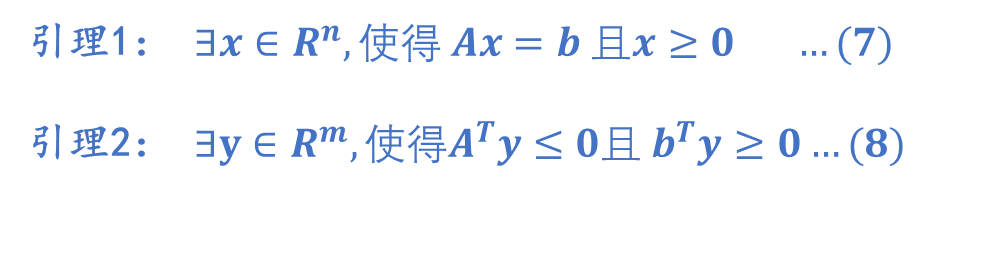
3.1 引理一: 向量b在凸锥C内
矩阵 由n个m维的列向量组成
向量 由n个非负标量组成
的非负系数的线性组合是一个凸锥C
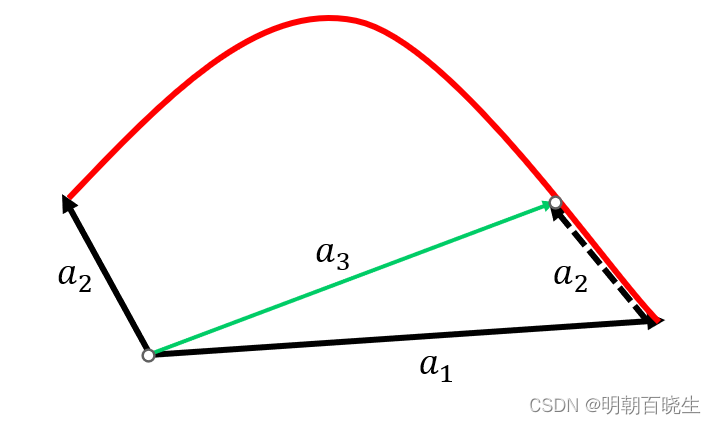
如上图:
两个向量顶点连接起来可以组成一个凸锥C,
两者通过非负的线性系数相加得到的 也一定落在该凸锥C 内
同理:
非负的线性组合 组成了凸锥C,b由该非负的线性组合得到,也落在该凸锥C内.
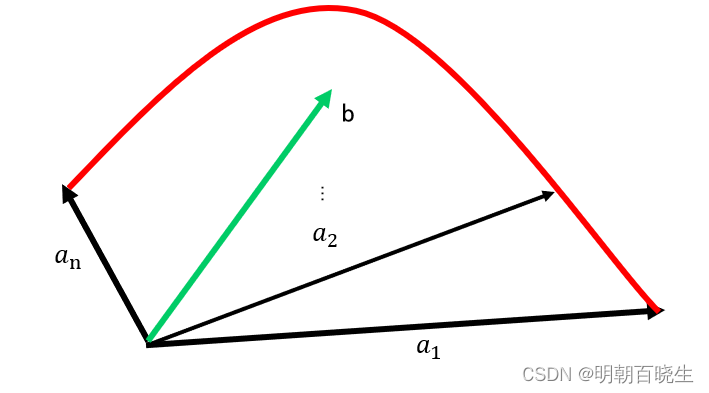
3.2 引理二 :b在凸锥C外
: 、
向量y在凸锥C外,向量y与该凸锥C中任意向量夹角大于90
:
,向量 b,y 夹角小于90度, 所以向量b 在凸锥C外
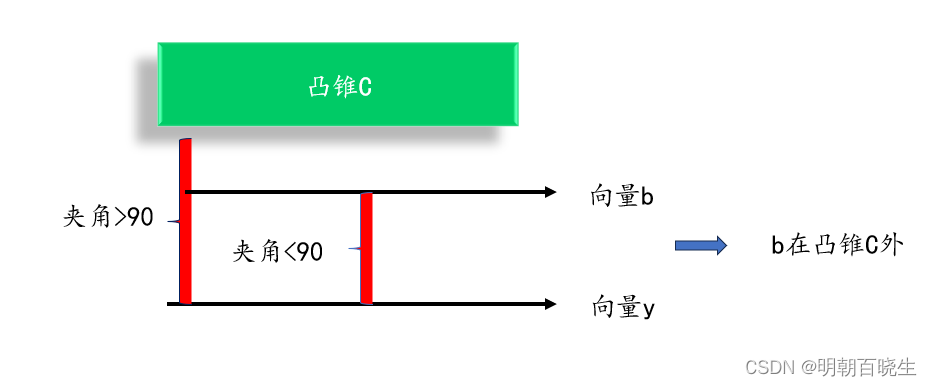
也可以用下图表示
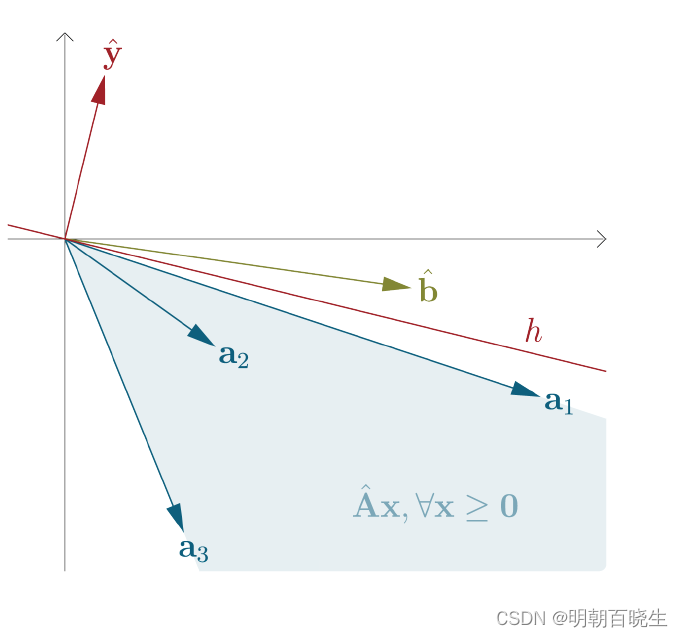
四 强对偶(Strong Duality)

Farkas 两条引理:
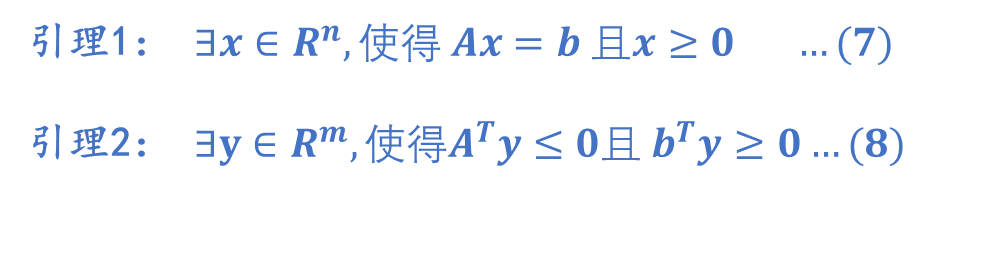
我们要利用Farkas 两条引理 , 证明的是 可以无限接近
证明:
假设原始问题的最优解为,我们定义:
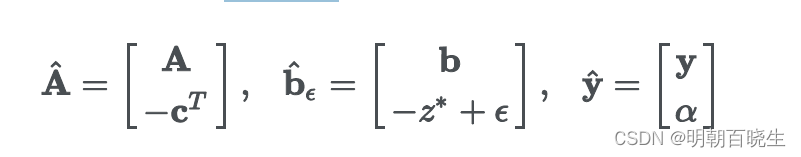
其中
4.1 当 时,满足 Farkas case (1)
因为
不满足Farkas case(2) 即
,
....(9)
4.2 时,满足Farkas case(2)
. 因为 已经是最小值了,不存在非负解,使得
(EMD为非负的值)
所以Farkas case(1) 不成立, Farkas case(2) 成立。
存在 使得
且
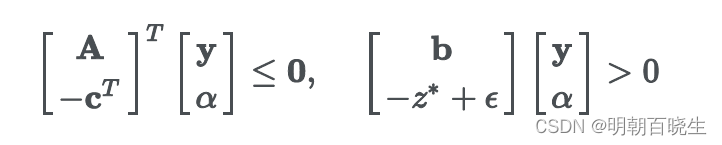
等价于: 推理2,推理3
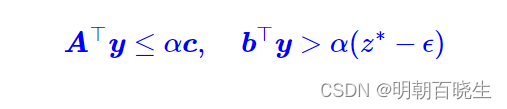 ...(10)
...(10)
,
...(11)
当 , 根据式(9)
, 式(11)
得知,取
弱对偶形式:
则:
是任意的,两者可以无限接近,从而
五:传输成本的对偶
EMD 优化目标
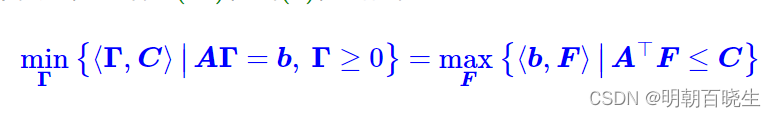
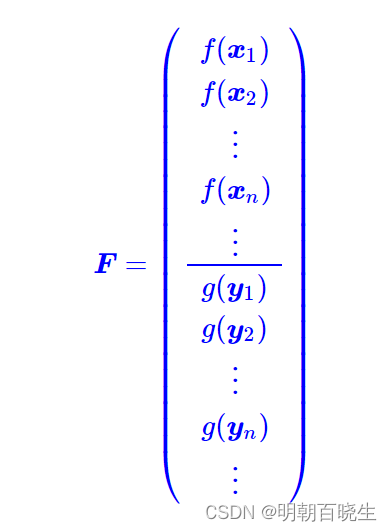
GAN 在图像处理里面,状态变量 x,和y 的范围一致,所以EMD 优化目标可以写成如下:
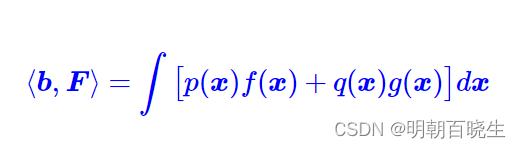
根据约束条件:
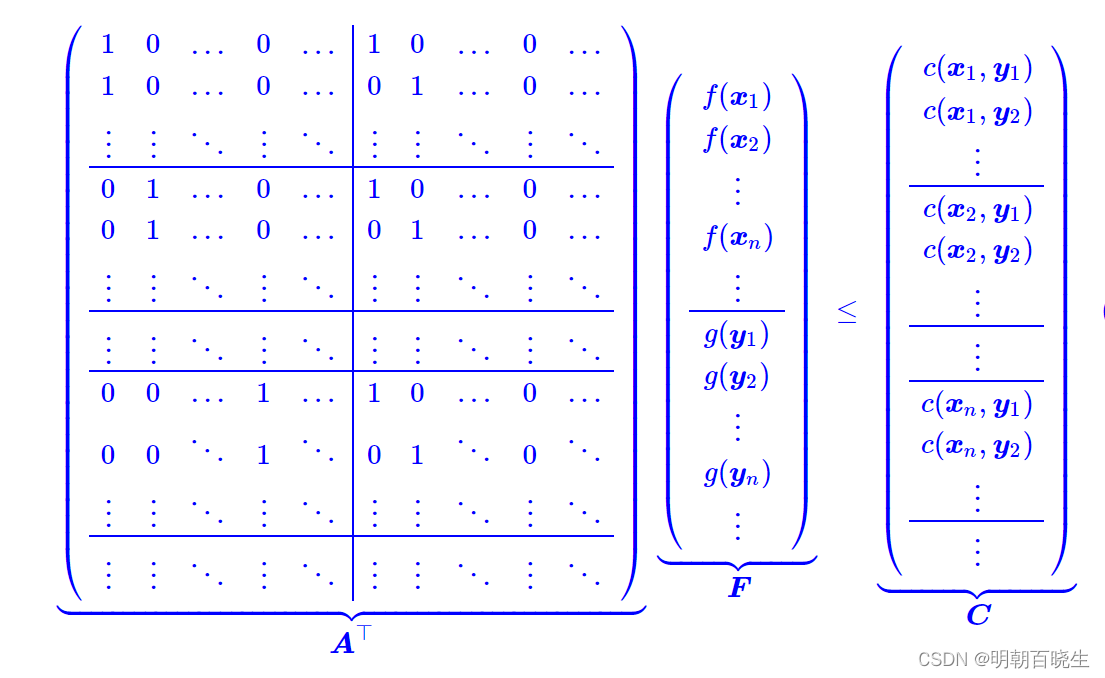

六 对偶到WGAN
我们得到最优传输成本的对偶形式
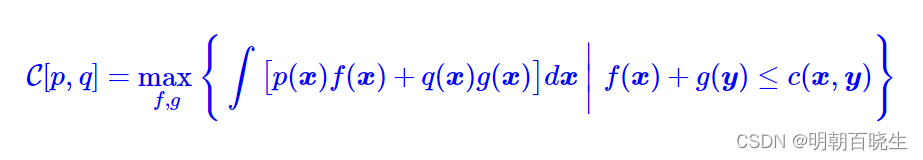
因为 , 同时
代表的是非负的概率(标量),所以
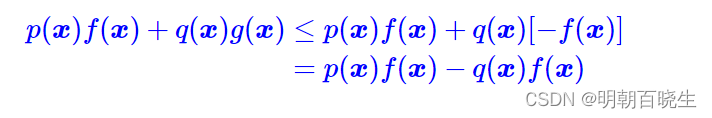
等价于求解
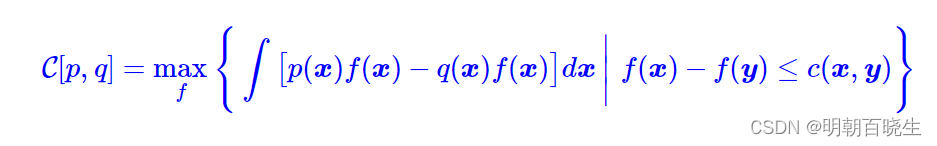
这便是我们最终要寻找的最优传输成本(1)的对偶形式了
当,我们有
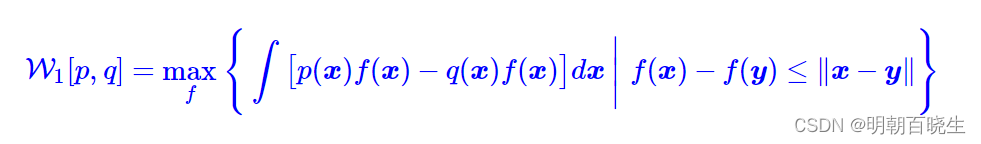
这就是WGAN所采用的W距离,于p,q 都是概率分布,因此我们可以写成采样形式
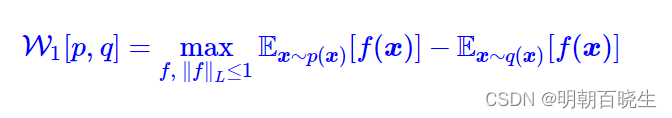
自然地,整个WGAN的训练过程就是
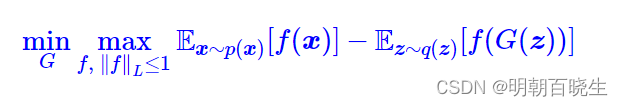
七 Lipschitz约束和Wasserstein 关系
7.1 Lipschitz 函数定义

当L =1 的时候 就是 WGAN的约束条件
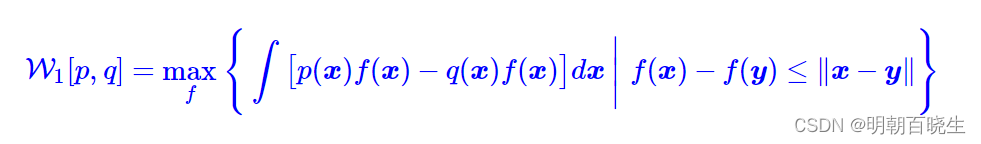
其中约束条件我们通常写为
参考:
20 AI Projects for Kids That Will Blow Their Minds
https://www.cnblogs.com/yhxm/p/13047489.html
python模块:Scipy.optimize.linprog线性规划求解-CSDN博客
CSDN
从Wasserstein距离、对偶理论到WGAN - 科学空间|Scientific Spaces