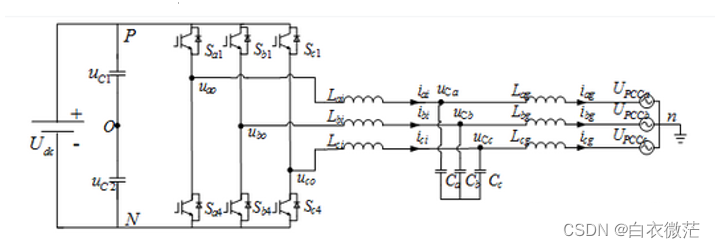
在逆变器并网系统中，并网电压前馈是整个系统中较为重要的一环，一方面，他可以在一定程度上增加系统的快速响应能力，另一方面，其可以 消除电网电压中的低次谐波对并网输出电流的影响，使得整个系统的并网电能质量显著提高，如下图所示
在弱电网下，电网阻抗不可忽略，而实际系统中的采样值并不是理想电压，其为电网阻抗上的电压与理想电压叠加而成，如下式所示：
而通过阻抗识别法，进行电网阻抗的识别，即Zg的识别，再通过对输出电流的采样，减去电网阻抗上的电压，即可实现在弱电网下，消除电网阻抗的耦合。如下图所示
逆变器专题（21）-并网电压前馈（消除弱电网影响）（1）
news2025/1/17 0:23:21
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1513414.html
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！相关文章
spring boot 学习
目录
引言：
一、Spring Boot概述
二、Spring Boot的核心特性
1 自动配置
2 起步依赖
3 内嵌容器
4 监控与管理
三、Spring Boot的入门步骤
1 环境安装
2 创建项建
3 编写代码
1 启动类
2 控制器
3服务
4自动装配
5配置属性
6 JPA实体
4 运行与调试…
【Linux】linux的常用命令
📝个人主页：五敷有你 🔥系列专栏：MQ
⛺️稳中求进，晒太阳 (Linux常用命令) finalShell
1. ls命令
作用：显示当前目录下的文件及文件夹
举例：在用户目录（root)使用ls可以查…
【Python】新手入门学习：详细介绍开放封闭原则（OCP）及其作用、代码示例
【Python】新手入门学习：详细介绍开放封闭原则（OCP）及其作用、代码示例 🌈 个人主页：高斯小哥 🔥 高质量专栏：Matplotlib之旅：零基础精通数据可视化、Python基础【高质量合集】、PyT…
网络通信另个角度的认识(进程间通信),端口号(为什么要有,和pid的关系,分类,如何封装,和进程的定位原理+对应关系),客户端如何拿到服务端的port
目录
另一个角度认识网络通信
端口号
引入 -- 为什么要有端口号
问题
解决
端口号和pid
举例
介绍
分类
知名端口
注册端口
动态端口
客户端如何知道服务端的端口号
封装端口号
定位原理
进程和端口号的对应关系
数据如何被上层进程读到 另一个角度认识网络…
汉诺塔问题代码写法的详细解析
汉诺塔游戏规则：
规则： 汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着…
基于Web的论文管理系统设计
目 录
目 录 III 摘 要 V 关键词 V Abstract VI Key Word VI 第一章 绪论 6 1.1系统设计背景 1 1.2系统设计目的与意义 1 1.3国内外现状 2 1.4本文结构 3 第二章 需求分析 3 2.1系统需求分析 4 2.2系统角色设计 4 第三章 系统开发技术 4 3.1 PHP语言简介和特点 5 3.2 Mysql数据…
代码随想录day18（1）二叉树：二叉树的层序遍历（leetcode102）
题目要求：实现二叉树的层序遍历
思路：实现层序遍历使用队列即可。每个结点遍历结束后，将其左右孩子结点也放入队列。本道题返回的是一个二维数组，即需要将每一层分开，所以还需要size变量记录每层元素个数。注意&#…
程序员来看，你选哪一门编程语言提升自己？
通过多个调查表的分析，发现大家对于GO语言的兴趣和需求非常高。GO语言是一种由Google开发的静态类型、编译型语言，最初于2007年问世。这门语言的设计者是Robert Griesemer、Rob Pike和Ken Thompson，他们的初衷是为了弥补C和Java在大规模软件工…
2024年3月9日美团笔试解答
这题打卡题，先扫描一遍原本有n个M和T，然后总数减一下，剩下m个，再看可以添加k个，返回nmin(m,k)
Python解答
import time
import bisect
import functools
import math
import os
import random
import re
import sys
…
Linux 动态库和静态库 【详解】
动静态库的基本原理
静态库（.a）：程序在编译链接的时候把库的代码链接到可执行文件中。程序运行的时候将不再需要静态库动态库（.so）：程序在运行的时候才去链接动态库的代码，多个程序共享使用库的…
uniapp使用openlayers加载地图服务
uniapp使用openlayers加载地图服务 <!-- 地图组件 -->
<template><view id"myMap" :regionChangeItem"regionChangeItem" :change:regionChangeItem"olRender.selectAdministrativeRegion":tagSelectProducetagSelectProduce :ta…
数字图像处理 使用C#进行图像处理九 实现傅里叶变换
一、简述 傅立叶变换将图像分解为其正弦和余弦分量。换句话说，它将图像从空间域变换到频率域。这个想法是任何函数都可以用无限正弦函数和余弦函数之和来精确近似。傅里叶变换是实现此目的的一种方法。 网上有很多关于傅里叶变换的文章，这里就不进行赘述了，这里主要结合代码…
JS：36种原生JS数组方法（8种改变原数组方法，28种不涉及数组改变的方法）
一、改变原数组方法
1.push()
作用：向数组的末尾添加一个或多个元素
返回：添加后数组的长度。 <script>let arr [1, 2, 3];console.log(arr.push(4)); //4console.log(arr); //[1, 2, 3, 4]console.log(arr.push(2, 4)); //6console.log(arr);…
cad转shp再转3dtiles生成白模
1、准备CAD数据
2、arcgis中添加cad数据
添加面 cad中的标高字段是能带进arcgis中的，如果这个数据是建筑高度，可以直接用了
3、转shp 4、shp转3dtiles白模
cesiumlab中shp转3dtiles白模效果一
新零售SaaS架构：什么是线上商城系统？
零售商家为什么要建设线上商城 传统的实体门店服务范围有限，只能吸引周边500米内的消费者。因此，如何拓展服务范围，吸引更多消费者到店，成为了店家迫切需要解决的问题。
缺乏忠实顾客，客户基础不稳，往往是…
buuctf warmup
1.代码审计：
<?phphighlight_file(__FILE__);class emmm //定义了一个类{public static function checkFile(&$page) 类里面又申明创建了一个函数{$whitelist ["source">"source.php","…
安装汇春MDTIDE以及HI-TECH PICCv9.83(PICC语言编译器)
最近了解了汇春一款8位通用型MCU----MDT10F684，所以这里安装一下IDE以及配置一下环境。
1.安装汇春MDTIDE 去到官网下载对应的开发包，我不知道里面内容是否一致。
Flash/MTP MCU (yspringtech.com)
不要点说明书下载，点了没反应࿰…
借助ChatGPT提高编程效率指南
PS: ChatGPT无限次数，无需魔法，登录即可使用,网页打开下面
一、借助ChatGPT提高编程效率指南 随着计算机技术的飞速发展，编程已经成为了现代社会中一个非常重要的技能。对于许多人来说，编程不仅是一项工作技能，而且是…