这题打卡题,先扫描一遍原本有n个M和T,然后总数减一下,剩下m个,再看可以添加k个,返回n+min(m,k)
- Python解答
import time
import bisect
import functools
import math
import os
import random
import re
import sys
import threading
from collections import Counter, defaultdict, deque
from copy import deepcopy
from functools import cmp_to_key, lru_cache, reduce
from heapq import heapify, heappop, heappush, heappushpop, nlargest, nsmallest
from io import BytesIO, IOBase
from itertools import accumulate, combinations, permutations
from operator import add, iand, ior, itemgetter, mul, xor
from string import ascii_lowercase, ascii_uppercase
from typing import *
input = lambda: sys.stdin.readline().rstrip("\r\n")
n, k = map(int, input().split())
s = input()
ans = 0
tot = 0
for i, c in enumerate(s):
if not(c == "M" or c == "T"):
tot += 1
if k >= tot:
print(n)
else:
print(n - tot + k)


依旧是打卡题,最大最小理所应当的是当未知数分别取l和r时成立。
import sys
input = lambda: sys.stdin.readline().rstrip("\r\n")
n, q = list(map(int, input().split()))
a = list(map(int, input().split()))
tot = sum(a)
numa = sum([1 if x == 0 else 0 for x in a])
for _ in range(q):
l, r = list(map(int, input().split()))
print(numa * l + tot, numa * r + tot)

本题解法为二维前缀和,数据量较小,前缀和+暴力就行了,第一遍扫描的时候统计左上角顶点为(0,0),右下角顶点为(i,j)的矩形中0-1的差值,map[i][j]=map[i-1][j]+map[i][j-1]-map[i-1][j-1]的0和1。第二遍扫描的时候左下角差值和右上角差值进行比较就行了,时间复杂度O(n3)
import sys
input = lambda: sys.stdin.readline().rstrip("\r\n")
n = int(input())
g = [[] for _ in range(n)]
for i in range(n):
s = input()
for c in s:
g[i].append(int(c))
prefix = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(n):
for j in range(n):
prefix[i + 1][j + 1] = prefix[i][j + 1] + prefix[i + 1][j] - prefix[i][j] + g[i][j]
def work(k):
cnt = 0
for i in range(k, n + 1):
for j in range(k, n + 1):
di, dj = i - k, j - k
tot = prefix[i][j] - prefix[i][dj] - prefix[di][j] + prefix[di][dj]
if tot == k * k // 2:
cnt += 1
return cnt
for i in range(n):
if (i + 1) % 2 == 1:
print(0)
else:
print(work(i + 1))


首先,想要得到末尾是0就必须有一对2和5,简单的数学知识。然后接下来有两种解法,第一是使用线段树,查找每个区域2和5的数量,不过这里不需要,且时间复杂度比第二种高;第二种使用前缀和+双指针,可以优化到O(n)复杂度。
具体看注释
import java.util.*;
import java.util.stream.Stream;
import java.lang.Math;
public class Main {
# 寻找有多少2
private static int getTwoNum(int x){
int ct =0;
while (x % 2 == 0){
ct++;
x/=2;
}
return ct;
}
# 寻找有多少5
private static int getFiveNum(int x){
int ct =0;
while (x % 5 == 0){
ct++;
x/=5;
}
return ct;
}
public static void main(String[] args){
Scanner in = new Scanner(System.in);
while (in.hasNext()) {
int n = in.nextInt();
int k = in.nextInt();
int[] arrsTwoNum = new int[n];
int[] arrsFiveNum = new int[n];
int totTwoNum = 0; int totFiveNum = 0;
for (int i = 0; i < n; i++){
int x = in.nextInt();
arrsTwoNum[i] = getTwoNum(x);
arrsFiveNum[i] = getFiveNum(x);
totTwoNum += arrsTwoNum[i];
totFiveNum += arrsFiveNum[i];
}
if (totTwoNum < k || totFiveNum < k){
System.out.println(0);
return;
}
int rangeMaxTwoNum = totTwoNum-k; #最大可用删除的2的数量
int rangeMaxFiveNum = totFiveNum-k;#最大可用删除的5的数量
int ans = 0;
#前缀和,统计到i为止2和5的数量
for (int i = 1; i < n; i++){
arrsTwoNum[i]+=arrsTwoNum[i-1];
arrsFiveNum[i]+=arrsFiveNum[i-1];
}
int j = 0; 快指针
while (j < n && arrsTwoNum[j]<=rangeMaxTwoNum && arrsFiveNum[j]<= rangeMaxFiveNum){
j++;
}
ans += j; #每次快指针使得段内2和5超标,更新一次ans
for (int i = 0; i < n; i++){
while (j < n && arrsTwoNum[j]-arrsTwoNum[i]<=rangeMaxTwoNum && arrsFiveNum[j]-arrsFiveNum[i]<= rangeMaxFiveNum){
j++;
}
ans+=(j-i-1);
}
System.out.println(ans);
}
}
}

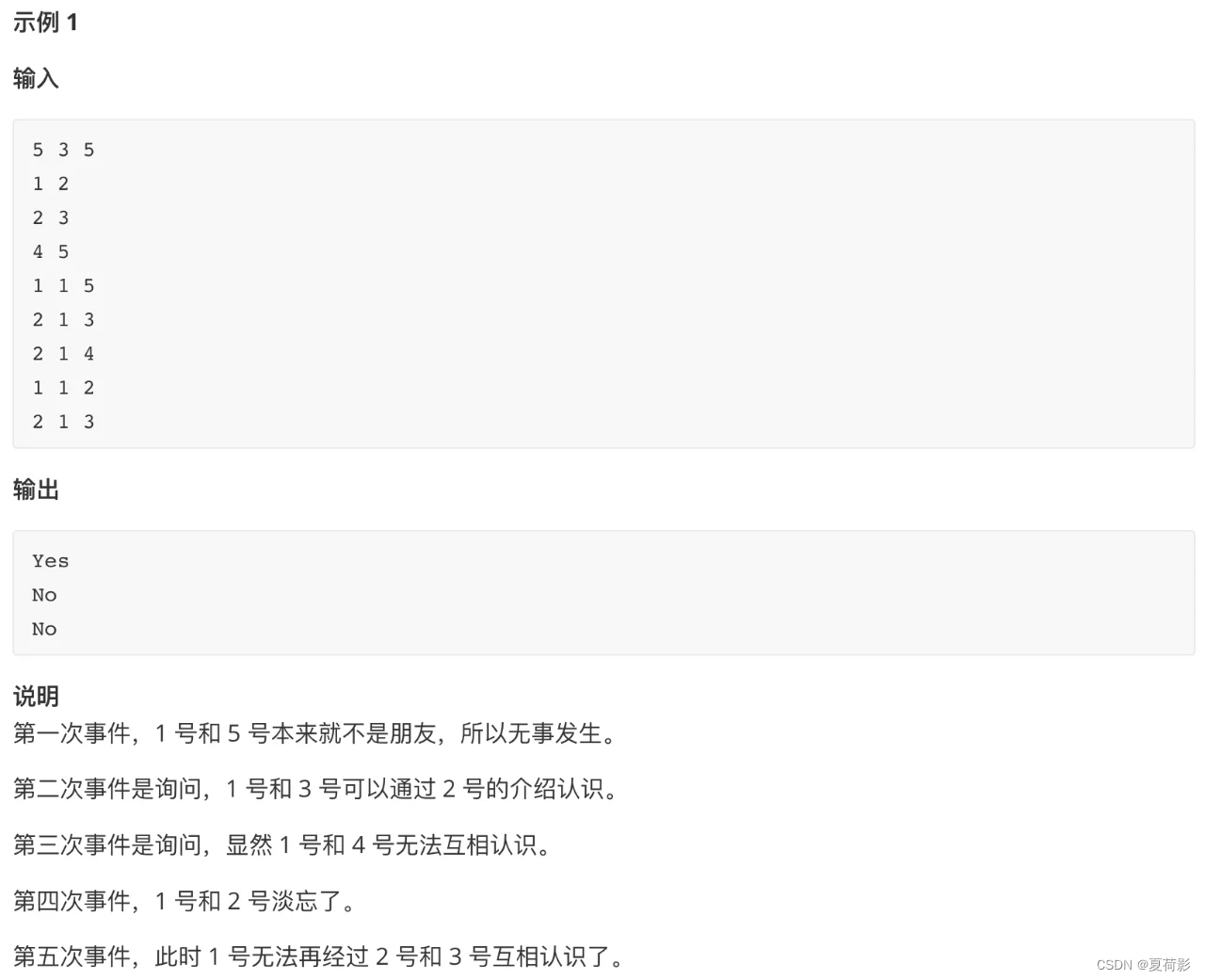
压轴题,帮美团笔试挽尊。但是不要被109的节点数量级骗了,注意边最多只有105,也就是存在大量节点是孤立的,筛选后需要考虑的也就105数量级。
很显然,检查两个节点是否连接的话,使用最小连通图的算法时间复杂度必然是不够的,而且我们也不需要知道二者之间有多少跳,只要使用并查集就行了。(不会并查集的可以直接跳了,先去学并查集)
但是并查集存在一个问题,就是当每次删除一条边之后,无法直接判断有没有出现新的集合。而我们也不可能每次删掉边之后重新计算一遍集合,该时间复杂度无法接受O(qm)。
但是,本题不要以流处理的想法来思考,而是应当看清,这题是批处理的题目。换句话说,我们可以把减法变为加法,倒过来计算每一次查询。而对于并查集而言,每次加入一条边,进行合并的复杂度仅为O(1).
import sys
from copy import deepcopy
from collections import defaultdict
input = lambda: sys.stdin.readline().rstrip("\r\n")
class DSU:
def __init__(self, n):
self.p = list(range(n))
self.size = [1] * n
def find(self, x):
if x != self.p[x]:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, x, y):
x, y = self.p[x], self.p[y]
if x == y: return
if self.size[x] > self.size[y]:
x, y = y, x
self.size[y] += self.size[x]
self.p[x] = y
n, m, q = map(int, input().split())
# 先把有关系的人放到一起,然后离散化一下即可,没有关系的不用管
f = set()
all = defaultdict(int)
ct = 0
for _ in range(m):
u, v = map(int, input().split())
if u > v: u, v = v, u
if u not in all:
all[u] = ct
ct+=1
if v not in all:
all[v] = ct
ct += 1
ops = []
opuv = set()
for _ in range(q):
op, u, v = map(int, input().split())
if u > v:
u, v = v, u
ops.append((op, u, v))
# 如果是删除操作,记录到opuv
if op == 1:
opuv.add((u, v))
if u not in all:
all[u] = ct
ct += 1
if v not in all:
all[v] = ct
ct += 1
# print(all)
ans = []
# 先把后面的删除,然后建立并查集,然后倒着加边,如果不在原来的关系里面的边,不用加进去
fc = deepcopy(f)
for u, v in opuv:
if (u, v) in fc:
fc.remove((u, v))
m = len(all)
uf = DSU(m)
# print(f, fc)
for u, v in fc:
u, v = all[u], all[v]
uf.union(u, v)
ops = ops[::-1]
# print(ops)
for op, u, v in ops:
if u > v: u, v = v, u
idu, idv = all[u], all[v]
if op == 2:
idu, idv = uf.find(idu), uf.find(idv)
if idu == idv:
ans.append("Yes")
else:
ans.append("No")
else:
# 如果当前的这个不在f中,比如说1,5就不用加进去
if (u, v) in f:
uf.union(idu, idv)
for a in range(len(ans)-1,-1,-1):
print(ans[a])