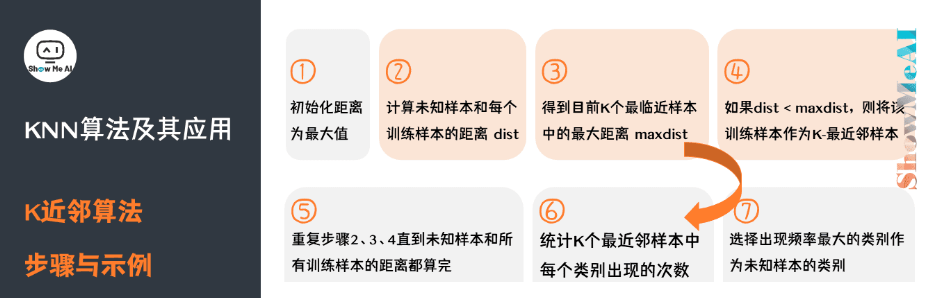
总结
本系列是机器学习课程的系列课程,主要介绍机器学习中分类算法,本篇为分类算法与knn算法部分。
本门课程的目标
完成一个特定行业的算法应用全过程:
懂业务+会选择合适的算法+数据处理+算法训练+算法调优+算法融合
+算法评估+持续调优+工程化接口实现
参考
KNN算法(k近邻算法)原理及总结
图解机器学习 | KNN算法及其应用
数据科学中常见的9种距离度量方法,内含欧氏距离、切比雪夫距离等
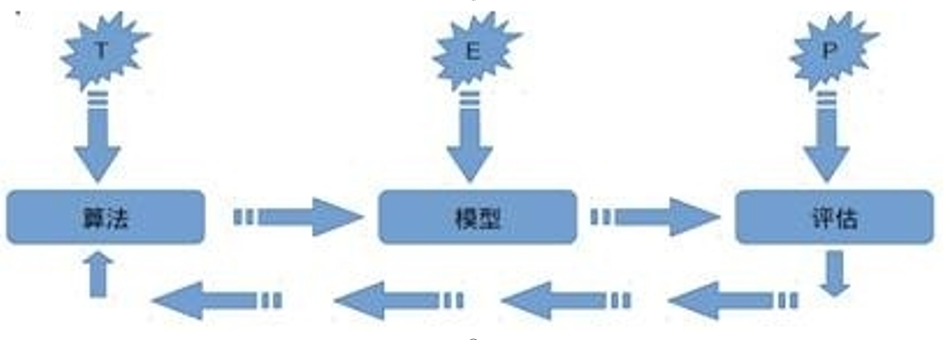
机器学习定义
关于机器学习的定义,Tom Michael Mitchell的这段话被广泛引用:
对于某类任务T和性能度量P,如果一个计算机程序在T上其性能P随着经验E而自我完善,那么我们称这个计算机程序从经验E中学习。
KNN算法
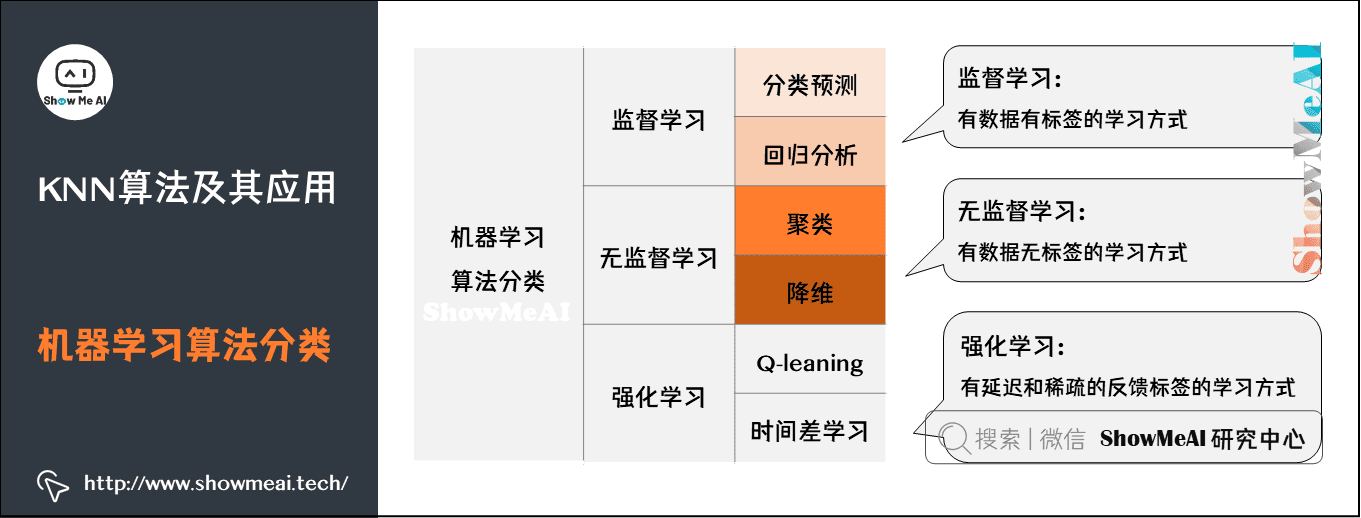
分类问题
分类问题是机器学习非常重要的一个组成部分,它的目标是根据已知样本的某些特征,判断一个样本属于哪个类别。分类问题可以细分如下:
二分类问题:表示分类任务中有两个类别新的样本属于哪种已知的样本类。
多类分类(Multiclass classification)问题:表示分类任务中有多类别。
多标签分类(Multilabel classification)问题:给每个样本一系列的目标标签。
分类问题的数学抽象
从算法的角度解决一个分类问题,我们的训练数据会被映射成n维空间的样本点(这里的n就是特征维度),我们需要做的事情是对n维样本空间的点进行类别区分,某些点会归属到某个类别。
下图所示的是二维平面中的两类样本点,我们的模型(分类器)在学习一种区分不同类别的方法,比如这里是使用一条直线去对两类不同的样本点进行切分。
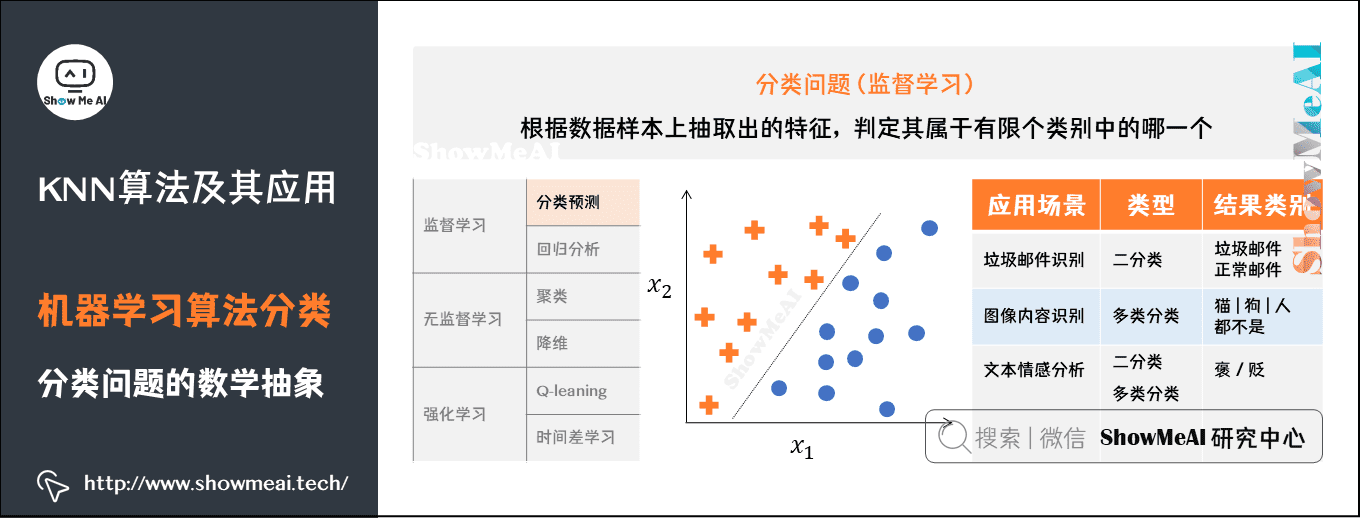
常见的分类问题应用场景很多,我们选择几个进行举例说明:
垃圾邮件识别:可以作为二分类问题,将邮件分为你「垃圾邮件」或者「正常邮件」。
图像内容识别:因为图像的内容种类不止一个,图像内容可能是猫、狗、人等等,因此是多类分类问题。
文本情感分析:既可以作为二分类问题,将情感分为褒贬两种,还可以作为多类分类问题,将情感种类扩展,比如分为:十分消极、消极、积极、十分积极等。
KNN简介
近邻算法(K-nearest neighbors,KNN ,有些地方也译作「 近邻算法」)是一种很基本朴实的机器学习方法。
KNN 在我们日常生活中也有类似的思想应用,比如,我们判断一个人的人品,往往只需要观察他最密切的几个人的人品好坏就能得到结果了。这就是 KNN 的思想应用,KNN 方法既可以做分类,也可以做回归。
在模式识别领域中, 近邻算法( KNN 算法,又译 最近邻算法)是一种用于分类和回归的非参数统计方法。在这两种情况下,输入包含特征空间中的 个最接近的训练样本。
1)K近邻核心思想
在 KNN 分类中,输出是一个分类族群。一个对象的分类是由其邻居的「多数表决」确定的,K个最近邻居(K为正整数,通常较小)中最常见的分类决定了赋予该对象的类别。
若K=1,则该对象的类别直接由最近的一个节点赋予。
在 KNN 回归中,输出是该对象的属性值。该值是其K个最近邻居的值的平均值。
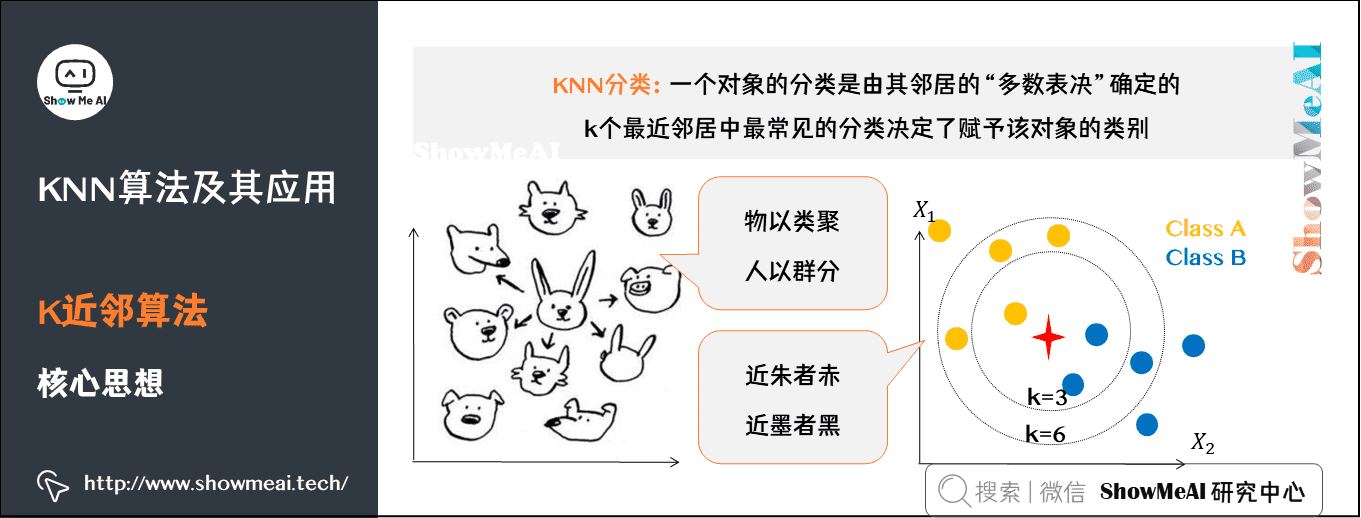
K近邻居法采用向量空间模型来分类,概念为相同类别的案例,彼此的相似度高。而可以借由计算与已知类别案例之相似度,来评估未知类别案例可能的分类。
KNN 是一种基于实例的学习,或者是局部近似和将所有计算推迟到分类之后的惰性学习。 近邻算法是所有的机器学习算法中最简单的之一。
KNN思想
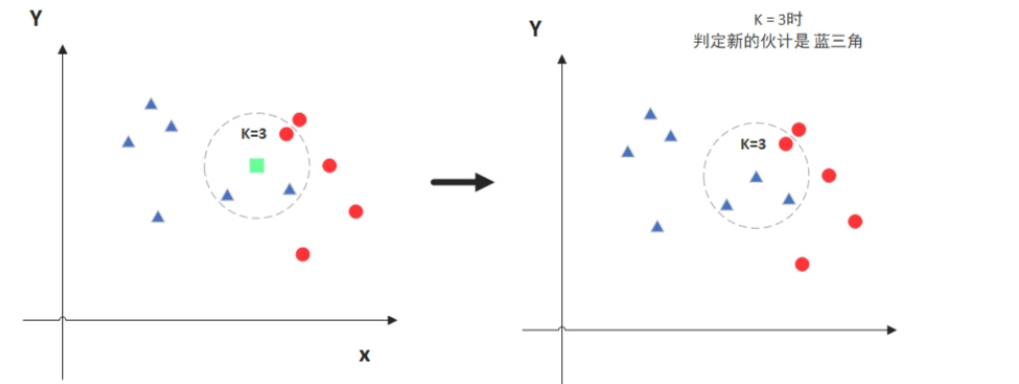
图中绿色的点就是我们要预测的那个点,假设K=3。那么KNN算法就会找到与它距离最近的三个点(这里用圆圈把它圈起来了),看看哪种类别多一些,比如这个例子中是蓝色三角形多一些,新来的绿色点就归类到蓝三角了。
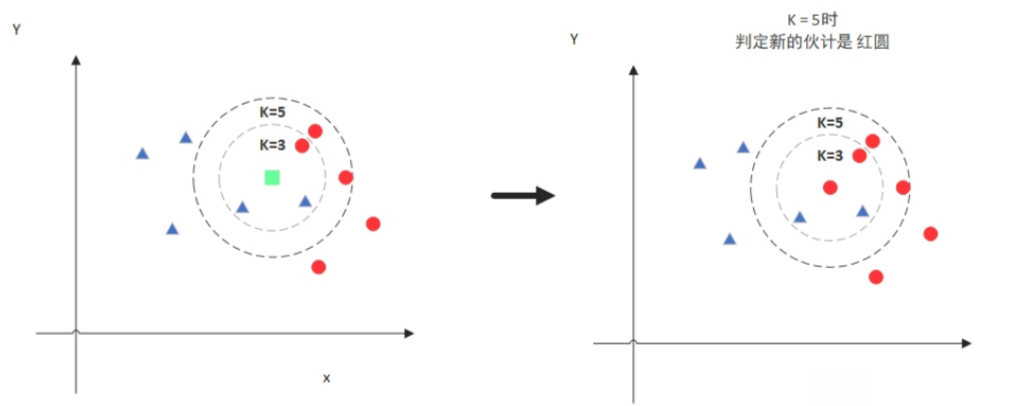
但是,当K=5的时候,判定就变成不一样了。这次变成红圆多一些,所以新来的绿点被归类成红圆。从这个例子中,我们就能看得出K的取值是很重要的。
K值的选取
我们可以通过交叉验证获得较好的k值,开始选取一个较小的K值,不断增加K值,然后计算验证集合的方差,最终找到一个比较合适的K值。如下图:
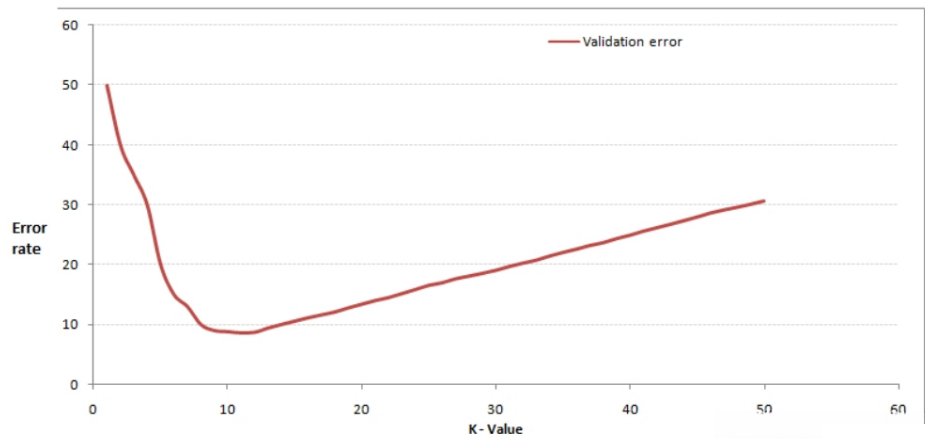
增大k的时候,一般错误率会先降低,因为有周围更多的样本可以借鉴了,分类效果会变好。当K值更大的时候,错误率会更高。比如说你一共就35个样本,当你K增大到30的时候,KNN基本上就没意义了。
所以选择K点的时候可以选择一个较大的临界K点,当它继续增大或减小的时候,错误率都会上升,比如图中的K=10。
点距离的计算
欧式距离
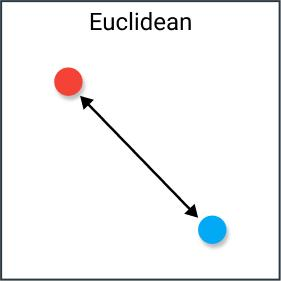
欧几里得距离:它也被称为L2范数距离。欧几里得距离是我们在平面几何中最常用的距离计算方法,即两点之间的直线距离。在n维空间中,两点之间的欧几里得距离计算公式为:


def euclidean_distance(x1, x2):
return math.sqrt(np.sum((x1 - x2)**2))
euclidean_distance函数计算多维空间中两点(x1和x2)之间的欧氏距离,函数的工作原理如下:
从x1元素中减去x2,得到对应坐标之间的差值。
使用**2运算将差值平方。
使用np.sum()对差的平方求和。
使用math.sqrt()取总和的平方根。
欧几里得距离是欧几里得空间中两点之间的直线距离。通过计算欧几里得距离,可以识别给定样本的最近邻居,并根据邻居的多数类(用于分类)或平均值(用于回归)进行预测。在处理连续的实值特征时,使用欧几里得距离很有帮助,因为它提供了一种直观的相似性度量。
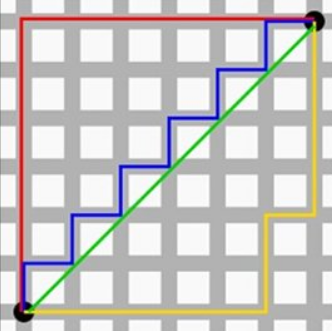
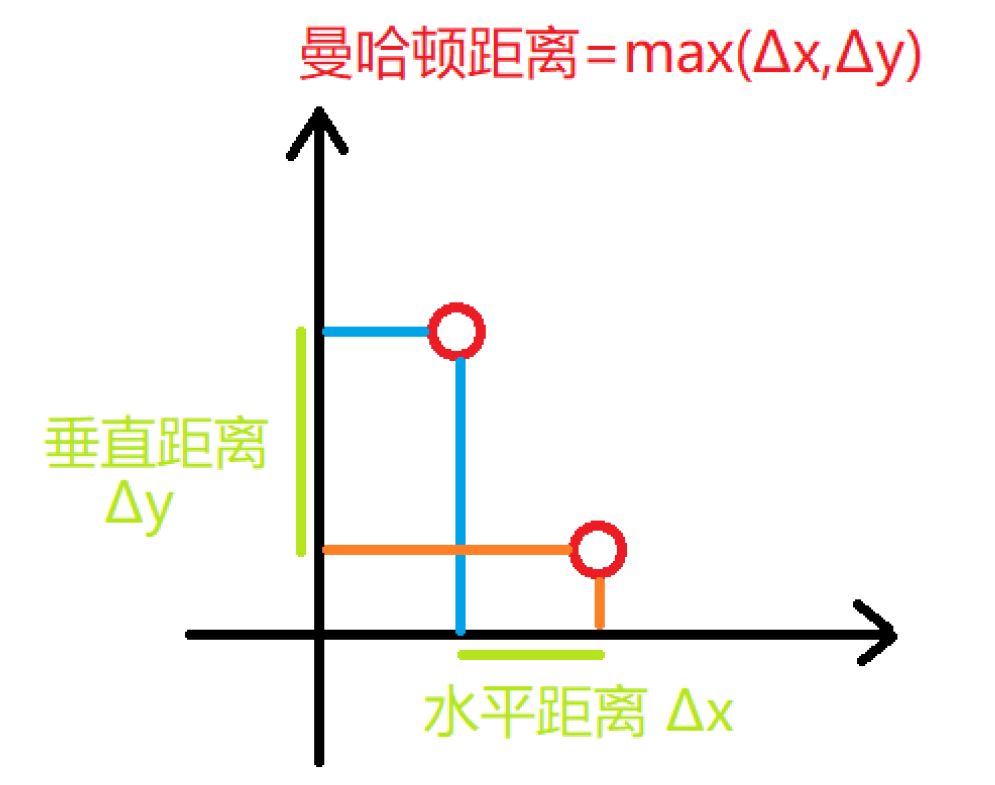
曼哈顿距离
KNN算法通常的距离测算方式为欧式距离和曼哈顿距离。

KNN 优缺点
KNN算法优点
简单易用,相比其他算法,KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
模型训练时间快,上面说到KNN算法是惰性的,这里也就不再过多讲述。
预测效果好。
对异常值不敏感
KNN算法缺点
对内存要求较高,因为该算法存储了所有训练数据
值的确定: KNN 算法必须指定K 值,K值选择不当则分类精度不能保证。
预测阶段可能很慢
对不相关的功能和数据规模敏感
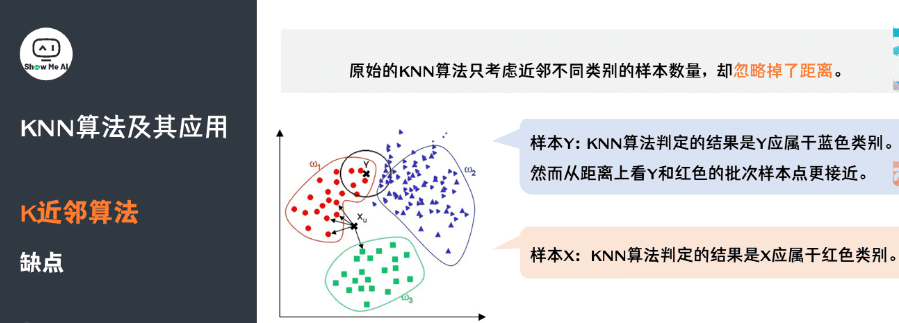
观察下面的例子,我们看到,对于样本 ,通过 KNN 算法,我们显然可以得到Y应属于红色类别。但对于样本 ,KNN 算法判定的结果是Y 应属于蓝色类别,然而从距离上看Y和红色的批次样本点更接近。因此,原始的 KNN 算法只考虑近邻不同类别的样本数量,而忽略掉了距离。
确定方向过程
针对完全没有基础的同学们
1.确定机器学习的应用领域有哪些
2.查找机器学习的算法应用有哪些
3.确定想要研究的领域极其对应的算法
4.通过招聘网站和论文等确定具体的技术
5.了解业务流程,查找数据
6.复现经典算法
7.持续优化,并尝试与对应企业人员沟通心得
8.企业给出反馈