1 红黑树（Red-Black Tree）

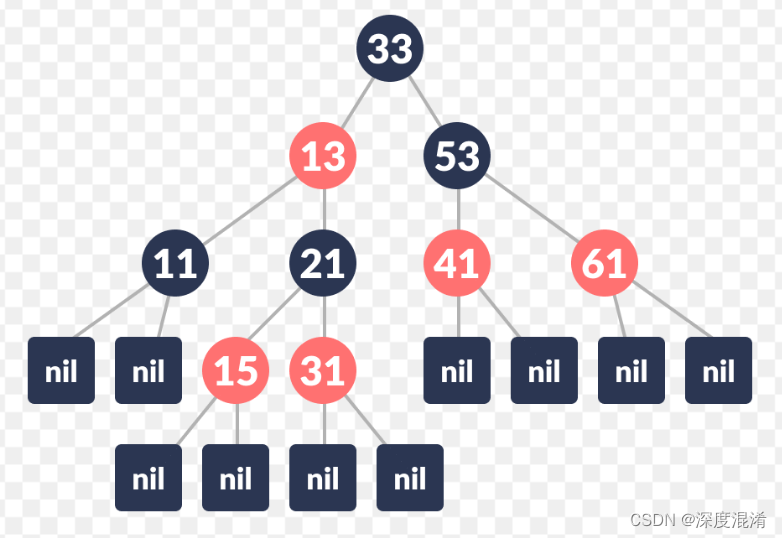
如果二叉搜索树满足以下红黑属性，则它是红黑树：

1. 每个节点不是红色就是黑色。
2. 根是黑色的。
3. 每片叶子（无）都是黑色的。
4. 如果一个节点是红色的，那么它的两个子节点都是黑色的。
5. 对于每个节点，从节点到后代叶的所有路径都包含相同数量的黑色节点。

红黑树是许多搜索树方案中的一种，它们是“平衡”的，
以便保证在最坏的情况下，基本的动态设置操作需要O（lg n）时间。
请注意，空叶节点或父节点的颜色为黑色。
更多细节请参见麻省理工学院出版社©2001《算法简介》，第二版，第13章（1180页）
托马斯·H·科尔曼、查尔斯·E·莱瑟森、罗纳德·L·里维斯特和克利福德·斯坦著

ISBN:0262032937

 Rudolf Bayer

2 红黑树的算法

红黑树（Red Black Tree） 是一种自平衡二叉查找树，是在计算机科学中用到的一种数据结构，典型的用途是实现关联数组。
红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。 
它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。
 

3 源程序

using System;
using System.Collections;
using System.Collections.Generic;

using Legalsoft.Truffer.TTree;

namespace Legalsoft.Truffer.Algorithm
{
    public class RedBlack_Tree
    {
        private BinaryNode root { get; set; } = null;

	public void Insert(int v)
        {
            BinaryNode node = new BinaryNode(v);
            if (root == null)
            {
                root = node;
            }
            else
            {
                BinaryNode tempX = root;
                BinaryNode tempY = null;
                while (tempX != null)
                {
                    tempY = tempX;
                    tempX = v.CompareTo(tempX.Key) > 0 ? tempX.Right : tempX.Left;
                }
                if (v.CompareTo(tempY.Key) >= 0)
                {
                    tempY.Right = node;
                }
                else
                {
                    tempY.Left = node;
                }
            }
            // 修复
            Insert_Fixup(node);
        }

        /// <summary>
        /// 删除节点。
        /// 如果节点只有一个子节点或没有子节点，只需将其删除即可。
        /// 如果节点同时具有左和右子节点，请找到其后续节点，删除它并复制其子节点、
        /// 要删除的节点的值。
        /// 删除后，根据定义修复树。
        /// </summary>
        /// <param name="node"></param>
        public void Delete(BinaryNode node)
        {
            if (node == null)
            {
                return;
            }
            if ((node == root) && (root.Right == null) && (root.Left == null))
            {
                root = null;
                return;
            }

            BinaryNode tempX = null;
            BinaryNode tempY = null;
            if (node.Left == null || node.Right == null)
            {
                tempY