题目1——01字符串

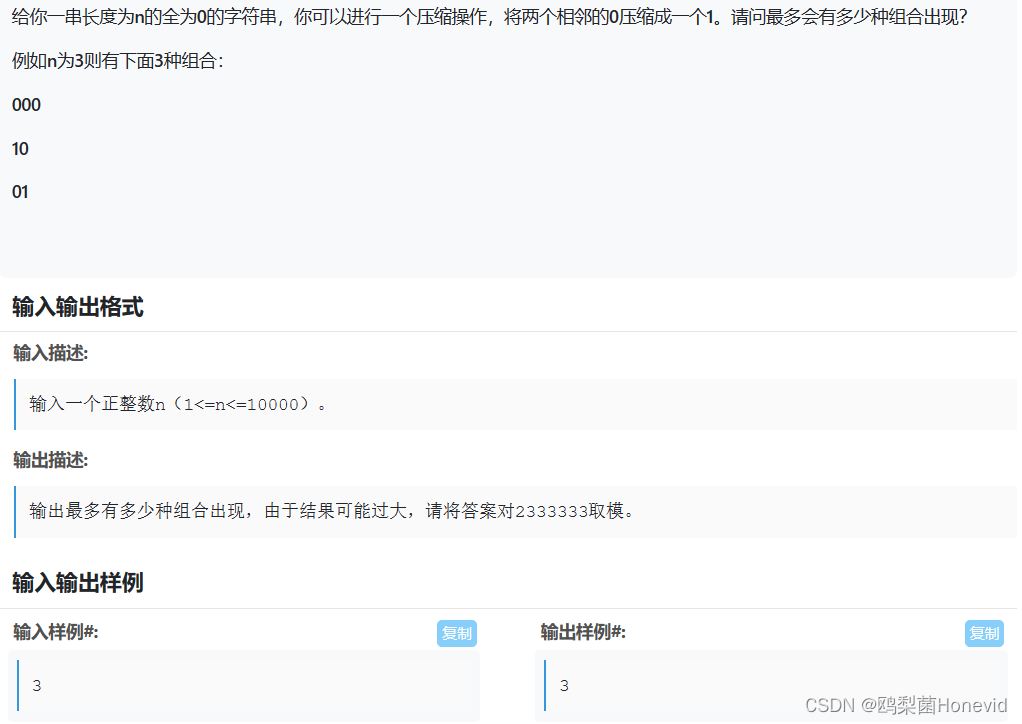
分析

经过拆解找规律，发现是两个斐波那契

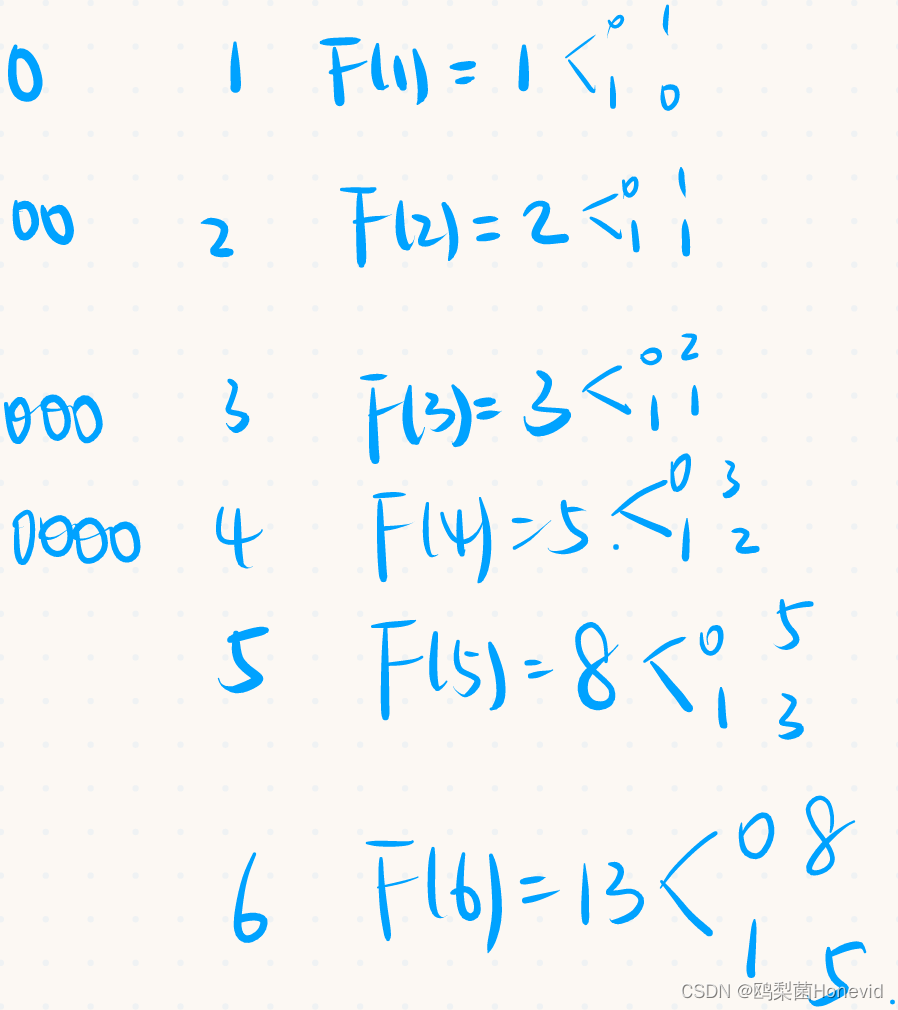
那么代码就好写了呀

#include <stdio.h>

unsigned long long f(int n){
	if(n==0||n==1){
		return n;
	}
	return (f(n-1)+f(n-2))%2333333;
}

int main(){
	int n;
	scanf("%d",&n);
	printf("%lld",f(n)+f(n-1));
}

注意！斐波那契是加法操作，每次取余再加和先加再取余，其实都不影响的，因此直接返回取余的值没有问题！！

题目2——非素数个数

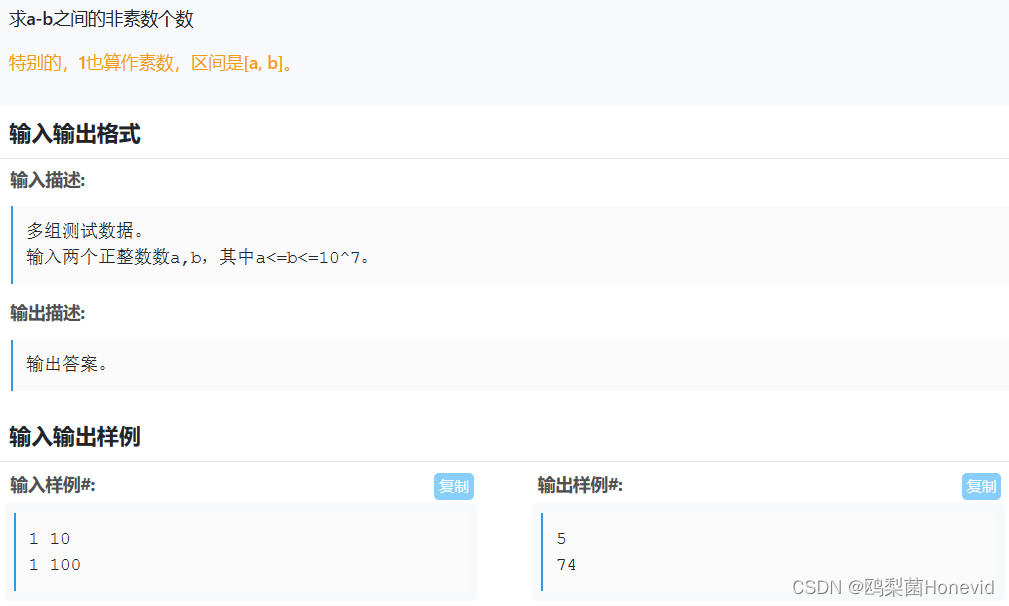
暴力解法，不多说

但是当达到10的7次量级，会超时

#include <cstdio>
#include <map>
#include <string>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> store;

bool is_su(int n){
  if(n==1||n==2||find(store.begin(),store.end(),n)!=store.end()){
    return true;
  }
  for(int i=2;i<=sqrt(n);i++){
    if(n%i==0){
      store.push_back(i);
      return false;
    }
  }
  return true;
}

int main(){
  int a,b;
  while(scanf("%d%d",&a,&b)!=EOF){
    int counts = b-a+1;;
    for(int i=a;i<=b;i++){
      if(is_su(i)==true){
        counts--;
      }
    }
    printf("%d\n",counts);
  }

	return 0;
}

用算法，没学过可能很难做出来

埃拉托斯特尼筛法是一种用于找出一定范围内所有素数的算法：
1.首先，创建一个包含从2到所需范围内所有数字的列表。
2.从最小的素数2开始，将其标记为素数，并将其倍数（除了自身）标记为合数。
3.继续找到下一个未被标记的素数，将其标记为素数，并将其倍数标记为合数。
4.重复步骤3，直到找到的素数的平方大于所需范围的最大值。
5.最后，未被标记为合数的数字即为素数。

#include <iostream>
using namespace std;
const int N = 1e7 + 10;

int a, b, cnt;
int primes[N];
bool st[N];

int get_primes(int x)
{
	for (int i = 2; i <= x; i ++ )
	{
		if (!st[i]) primes[cnt ++] = i;
		for (int j = 0; primes[j] <= x / i; j ++ )
		{
			st[primes[j] * i] = true;
			if (i % primes[j] == 0) break;
		}
	}
}

int main()
{
	get_primes(N);
	while (cin >> a >> b)
	{
		int res = 0;
		for (int i = a; i <= b; i ++ ) if (st[i]) res ++;
		cout << res << endl;
	}
	return 0;
}