122. 买卖股票的最佳时机 II

题目描述

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

示例 1：

输入：prices = [7,1,5,3,6,4]
输出：7
解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。

示例 2：

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。

示例 3：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

提示：

• 1 <= prices.length <= 3 * 10⁴
• 0 <= prices[i] <= 10⁴

贪心

这道题目可能我们只会想，选一个低的买入，再选个高的卖，再选一个低的买入…循环反复。

如果想到其实最终利润是可以分解的，那么本题就很容易了！

如何分解呢？

假如第 0 天买入，第 3 天卖出，那么利润为：prices[3] - prices[0]。

相当于(prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0])。

此时就是把利润分解为每天为单位的维度，而不是从 0 天到第 3 天整体去考虑！

那么根据 prices 可以得到每天的利润序列：(prices[i] - prices[i - 1]).....(prices[1] - prices[0])。

如图：

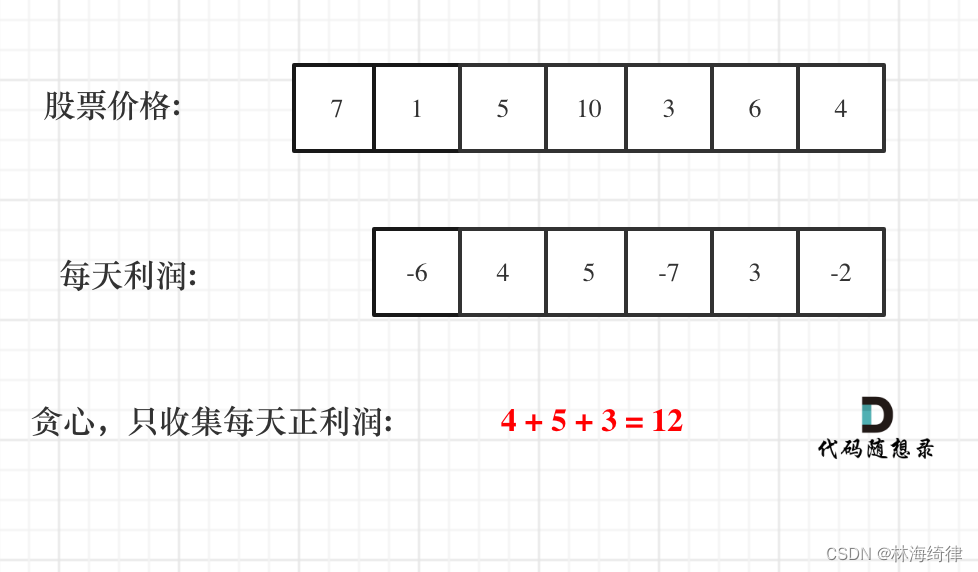
一些同学陷入：第一天怎么就没有利润呢，第一天到底算不算的困惑中。

第一天当然没有利润，至少要第二天才会有利润，所以利润的序列比股票序列少一天！

从图中可以发现，其实我们需要收集每天的正利润就可以，收集正利润的区间，就是股票买卖的区间，而我们只需要关注最终利润，不需要记录区间。

那么只收集正利润就是贪心所贪的地方！

局部最优：收集每天的正利润，全局最优：求得最大利润。

局部最优可以推出全局最优，找不出反例，试一试贪心！

对应 C++代码如下：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // 定义一个变量coust来累计总利润，初始化为0
        int coust=0;
        
        // 遍历给定的股票价格数组
        for(int i=1;i<prices.size();i++)
        {
            // 对于每一天，计算与前一天价格的差值，即当天的潜在利润
            // 如果这个差值大于0，意味着如果在前一天买入，今天卖出能赚取利润
            // 使用max函数确保只加入正利润，忽略亏损的情况
            coust+=max(prices[i]-prices[i-1],0);
        }
        // 返回累计的总利润
        return coust;
    }
};

代码注释解释：

1. 函数签名：int maxProfit(vector<int>& prices)，这个函数接受一个整数类型的向量prices作为参数，其中prices[i]表示第i天的股票价格，函数返回一个整数，代表最大可能获得的利润。

2. 利润累计变量：int coust=0;，这行代码定义了一个变量coust来存储和累计最终的利润，初始值为0。

3. 遍历股票价格：循环从第二个价格元素开始遍历（for(int i=1;i<prices.size();i++)），因为需要比较当前价格与前一天的价格。

4. 计算每日利润：在循环体内，代码coust+=max(prices[i]-prices[i-1],0);计算了如果在第i-1天买入，第i天卖出可以获得的利润。如果这个利润是负数（即prices[i]-prices[i-1] < 0），则不会对总利润coust产生影响，因为使用了max函数确保只累加正利润。

5. 返回结果：函数最终返回累计总利润coust。

这段代码的核心思想是遍历整个价格数组，只要发现今天的价格比昨天高，就假设昨天买入今天卖出，并将这个差值加到总利润上。这种方法基于贪心算法的思想，即每一步都取当前可获得的最大利润，从而达到总利润最大化。