隐马尔可夫模型(Hidden Markov Model, HMM)是一种统计模型，在语音识别、行为识别、NLP、故障诊断等领域具有高效的性能。

HMM是关于时序的概率模型，描述一个含有未知参数的马尔可夫链所生成的不可观测的状态随机序列，再由各个状态生成观测随机序列的过程。

HMM是一个双重随机过程---具有一定状态的隐马尔可夫链和随机的观测序列。

HMM随机生成的状态随机序列被称为状态序列；每个状态生成一个观测，由此产生的观测随机序列，被称为观测序列。

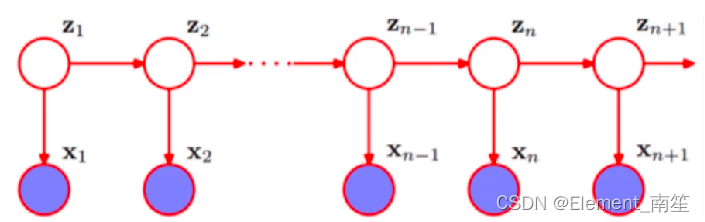
hmmlearn实现了隐马尔可夫模型 (Hidden Markov Models，简称 HMMs)。HMM 是一种生成概率模型，其中一系列可观测的变量由一系列内部隐藏状态生成。这些隐藏状态并不直接观察到。隐藏状态之间的转换被假定为（一阶）马尔可夫链的形式。它们可以通过起始概率向量和转移概率矩阵来指定。一个可观测值的发射概率可以是任何分布，其参数取决于当前的隐藏状态

 

import numpy as np
from hmmlearn import hmm
import math
states = ["Rainy", "Sunny"]##隐藏状态
n_states = len(states)##隐藏状态长度
  
observations = ["walk", "shop", "clean"]##可观察的状态
n_observations = len(observations)##可观察序列的长度
  
model = hmm.CategoricalHMM(n_components=n_states, n_iter=1000, tol=0.01)  #设置模型，和前两点不一样的就是设置训练轮数和阈值

X = np.array([[2, 0, 1, 1, 2, 0],[0, 0, 1, 1, 2, 0],[2, 1, 2, 1, 2, 0]])
model.fit(X)
print(model.startprob_)
print(model.transmat_)
print(model.emissionprob_)

from hmmlearn import hmm
import numpy as np
 
# 定义模型参数
states = ["Sunny", "Rainy"] #S

observations = ["Short-sleeved", "Long-sleeved"] #X
 
initial_probabilities = np.array([0.9, 0.1]) #Π初始矩阵

#A 转移矩阵
transition_probabilities = np.array([
    [0.8, 0.2],
    [0.3, 0.7]
])

#混淆矩阵B
emission_probabilities = np.array([
    [0.7, 0.3],
    [0.2, 0.8]
])
 
# 创建并训练HMM模型
model = hmm.MultinomialHMM(n_components=2,n_trials=1)
model.startprob_ = initial_probabilities
model.transmat_ = transition_probabilities
model.emissionprob_ = emission_probabilities
 
# 假设我们观察到的连续三天的衣服是: ["Short-sleeved", "Long-sleeved", "Long-sleeved"]
# 将其转化为多项分布的计数
obs_seq = np.array([
    [1, 0],  # Short-sleeved
    [0, 1],  # Long-sleeved
    [0, 1]  # Long-sleeved
])
 
# 使用Viterbi算法找到最可能的天气序列
logprob, state_seq = model.decode(obs_seq)
 
print("Observation sequence:", [observations[np.argmax(obs)] for obs in obs_seq])
print("Most likely weather sequence:", [states[i] for i in state_seq])

from hmmlearn import hmm
import numpy as np
 
# 定义模型参数
states = ["Sunny", "Rainy"] #S

observations = ["Short-sleeved", "Long-sleeved"] #X
 
initial_probabilities = np.array([0.9, 0.1]) #Π初始矩阵

#A 转移矩阵
transition_probabilities = np.array([
    [0.8, 0.2],
    [0.3, 0.7]
])

#混淆矩阵B
emission_probabilities = np.array([
    [0.7, 0.3],
    [0.2, 0.8]
])
 
# 创建并训练HMM模型
model = hmm.MultinomialHMM(n_components=2,n_trials=1)
model.startprob_ = initial_probabilities
model.transmat_ = transition_probabilities
model.emissionprob_ = emission_probabilities
 
# 假设我们观察到的连续三天的衣服是: ["Short-sleeved", "Long-sleeved", "Long-sleeved"]
# 将其转化为多项分布的计数
obs_seq = np.array([
    [1, 0],  # Short-sleeved
    [0, 1],  # Long-sleeved
    [0, 1]  # Long-sleeved
])
 
# 使用Viterbi算法找到最可能的天气序列
logprob, state_seq = model.decode(obs_seq)
 
print("Observation sequence:", [observations[np.argmax(obs)] for obs in obs_seq])
print("Most likely weather sequence:", [states[i] for i in state_seq])