---

1.背景

2017年，Mirjalili受到樽海鞘集群行为启发，提出了樽海鞘群算法(Salp Swarm Algorithm, SSA)。

2.算法原理

2.1算法思想

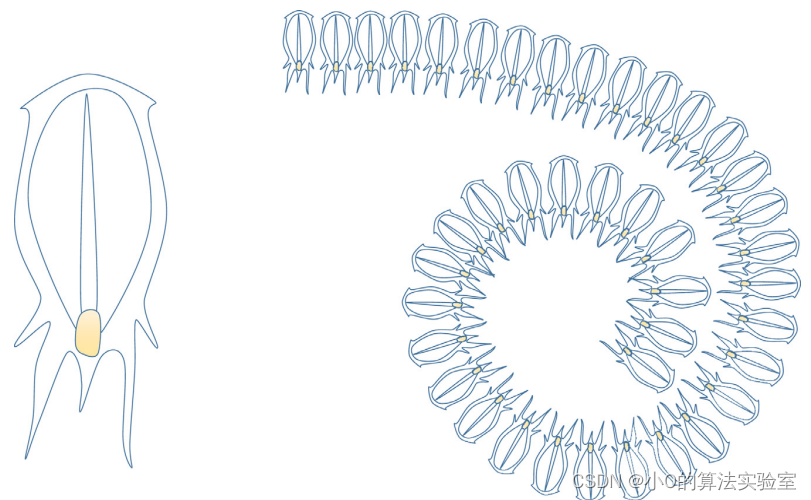
樽海鞘集群是领导者-追随者类型算法，整体以链式行为向食物移动。移动过程中，领导者进行全局探索，而追随者则充分进行局部探索。

2.2算法过程

领导者位置更新：
$$x^1=\{\begin{array}{llc}F+c_1\left(\left(ub-lb\right)c_2+lb\right)& c_3\ge 0& \\ F-c_1\left(\left(ub-lb\right)c_2+lb\right)& c_3<0& \end{array}$$
其中，$x^1,F$分别代表领导者位置和食物位置。参数$c_1$在算法中起到平衡全局探索和局部开发作用：
$$c_1=2e^{-{\left(\frac{4l}{L}\right)}^2}$$
参数$c_2,c_3$为[0,1]随机数，其实是为了增强随机性。
追随者位置更新：
由Newton运动定律，樽海鞘应满足：
$$x^i=\frac{1}{2}a{t}^2+{\nu }_{0}t$$
由于迭代次数是离散的，考虑到${\nu }_0=0$，因此可表述为：
$$x^i=\frac{1}{2}(x^i+x^{i-1})$$
🤣这里感觉有点问题：
$$\begin{gathered} a=\frac{dv}{dt} \\ v=\frac{dx}{dt} \end{gathered}$$
当$t$是离散且间隔为1时，此时$a=v_2-v_1,v2=x_2-x_1$，进一步有$a=x_2-2x_1+x_0$。
伪代码：

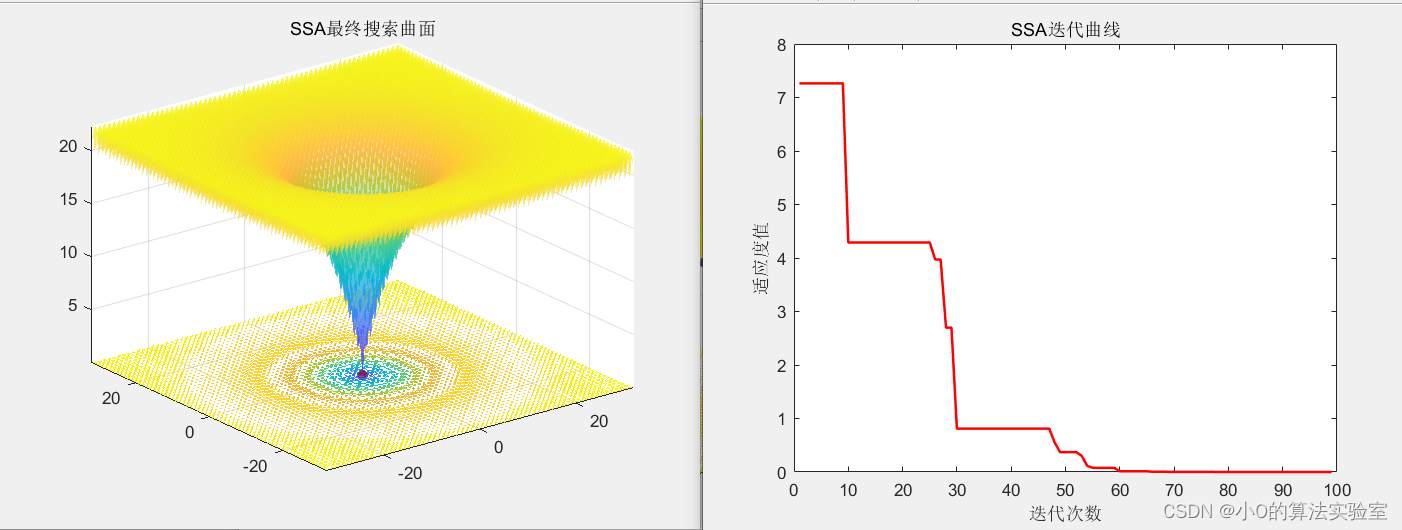
3.代码实现

% 樽海鞘群优化算法
function [Best_pos, Best_fitness, Iter_curve, History_pos, History_best] = SSA(pop, maxIter, lb, ub, dim,fobj)
%input
%pop 种群数量
%dim 问题维数
%ub 变量上边界
%lb 变量下边界
%fobj 适应度函数
%maxIter 最大迭代次数
%output
%Best_pos 最优位置
%Best_fitness 最优适应度值
%Iter_curve 每代最优适应度值
%History_pos 每代种群位置
%History_best 每代最优个体位置
%% 初始化种群
for i=1:dim
    SalpPositions(:,i) = lb(i)+rand(pop,1).*(ub(i) - lb(i));                          % Initial population
end
if size(ub,2)==1
    ub=ones(dim,1)*ub;
    lb=ones(dim,1)*lb;
else
    ub=ub';
    lb=lb';
end
%% 记录
Iter_curve = zeros(1,maxIter);
Best_pos=zeros(1,dim);
Best_fitness=inf;
%% 计算适应度
for i=1:size(SalpPositions,1)
    SalpFitness(1,i)=fobj(SalpPositions(i,:));
end
%% 记录
[sorted_salps_fitness,sorted_indexes]=sort(SalpFitness);
for newindex=1:pop
    Sorted_salps(newindex,:)=SalpPositions(sorted_indexes(newindex),:);
end

Best_pos=Sorted_salps(1,:);
Best_fitness=sorted_salps_fitness(1);

%% 迭代
l=2; 
while l<maxIter+1
    
    c1 = 2*exp(-(4*l/maxIter)^2); % Eq. (3.2)
    
    for i=1:size(SalpPositions,1)
        
        SalpPositions= SalpPositions';
        
        if i<=pop/2
            for j=1:1:dim
                c2=rand();
                c3=rand();
                % Eq. (3.1)
                if c3<0.5 
                    SalpPositions(j,i)=Best_pos(j)+c1*((ub(j)-lb(j))*c2+lb(j));
                else
                    SalpPositions(j,i)=Best_pos(j)-c1*((ub(j)-lb(j))*c2+lb(j));
                end
            end
            
        elseif i>pop/2 && i<pop+1
            point1=SalpPositions(:,i-1);
            point2=SalpPositions(:,i);
            
            SalpPositions(:,i)=(point2+point1)/2; % % Eq. (3.4) in the paper
        end
        
        SalpPositions= SalpPositions';
    end
    
    for i=1:size(SalpPositions,1)
        
        Tp=SalpPositions(i,:)>ub';Tm=SalpPositions(i,:)<lb';
        SalpPositions(i,:)=(SalpPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
        
        SalpFitness(1,i)=fobj(SalpPositions(i,:));
        
        if SalpFitness(1,i)<Best_fitness
            Best_pos=SalpPositions(i,:);
            Best_fitness=SalpFitness(1,i);
            
        end
    end
    
    Iter_curve(l)=Best_fitness;
    History_pos{l} = SalpPositions;
    History_best{l} = Best_pos;
    l = l + 1;
end
end

4.参考文献

[1] Mirjalili S, Gandomi A H, Mirjalili S Z, et al. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems[J]. Advances in engineering software, 2017, 114: 163-191.