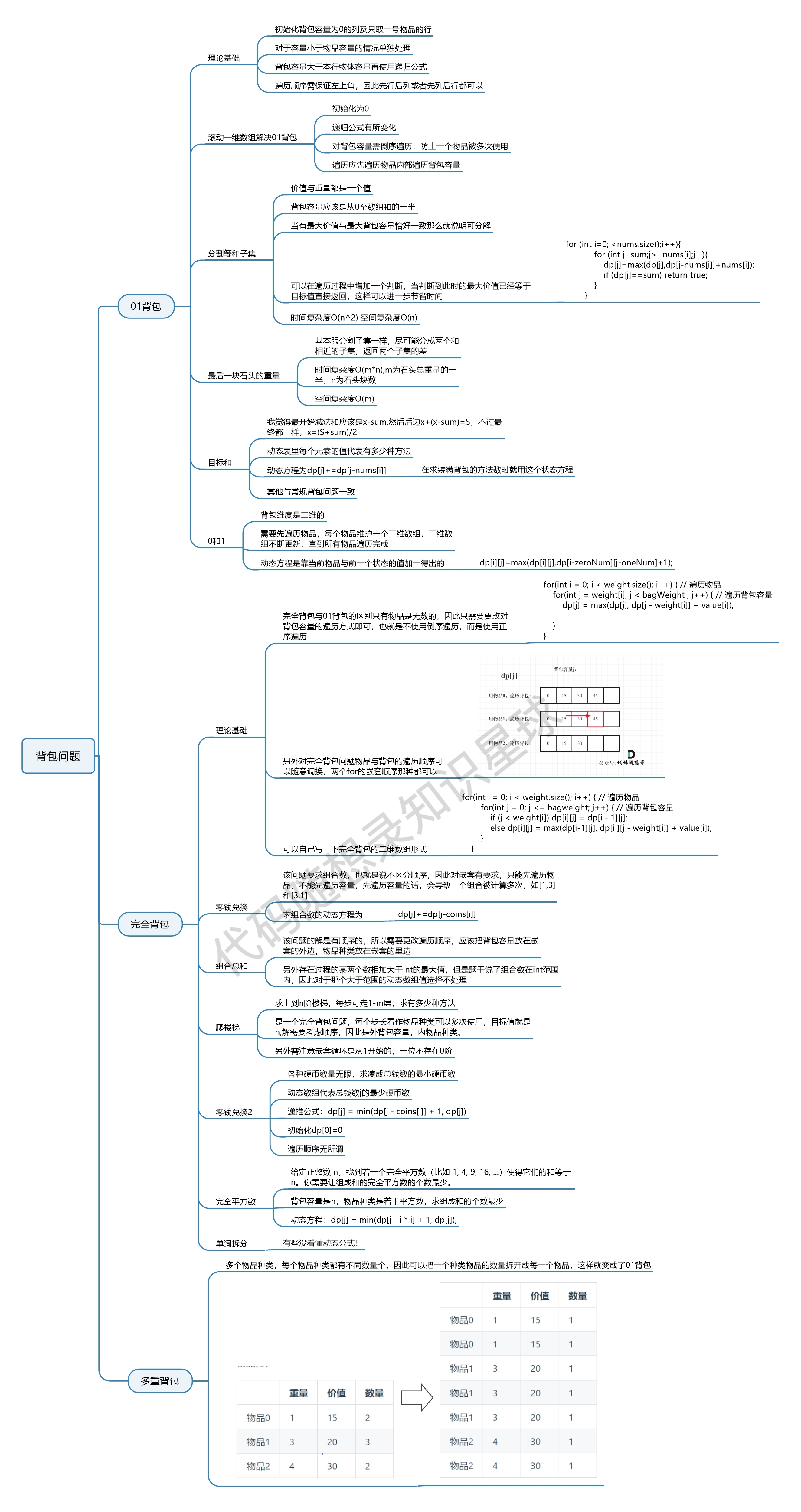
139.单词拆分
1、题目链接:. - 力扣(LeetCode)
2、文章讲解:代码随想录
3、题目:
给定一个非空字符串 s 和一个包含非空单词的列表 wordDict,判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。
说明:
拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。
示例 1:
- 输入: s = "leetcode", wordDict = ["leet", "code"]
- 输出: true
- 解释: 返回 true 因为 "leetcode" 可以被拆分成 "leet code"。
示例 2:
- 输入: s = "applepenapple", wordDict = ["apple", "pen"]
- 输出: true
- 解释: 返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
- 注意你可以重复使用字典中的单词。
示例 3:
- 输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
- 输出: false
4、视频链接:
动态规划之完全背包,你的背包如何装满?| LeetCode:139.单词拆分_哔哩哔哩_bilibili
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
HashSet<String> set = new HashSet<>(wordDict);
boolean[] valid = new boolean[s.length() + 1];
valid[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i && !valid[i]; j++) {
if (set.contains(s.substring(j, i)) && valid[j]) {
valid[i] = true;
}
}
}
return valid[s.length()];
}
}// 另一种思路的背包算法
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (String word : wordDict) {
int len = word.length();
if (i >= len && dp[i - len] && word.equals(s.substring(i - len, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}多重背包理论基础
对于多重背包,我在力扣上还没发现对应的题目,所以这里就做一下简单介绍,大家大概了解一下。
有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。
多重背包和01背包是非常像的, 为什么和01背包像呢?
每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
例如:
背包最大重量为10。
物品为:
| 重量 | 价值 | 数量 | |
| 物品0 | 1 | 15 | 2 |
| 物品1 | 3 | 20 | 3 |
| 物品2 | 4 | 30 | 2 |
问背包能背的物品最大价值是多少?
和如下情况有区别么?
| 重量 | 价值 | 数量 | |
| 物品0 | 1 | 15 | 1 |
| 物品0 | 1 | 15 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品1 | 3 | 20 | 1 |
| 物品2 | 4 | 30 | 1 |
| 物品2 | 4 | 30 | 1 |
毫无区别,这就转成了一个01背包问题了,且每个物品只用一次。
练习题目:卡码网第56题,多重背包(opens new window)
代码如下:
// 超时了
#include<iostream>
#include<vector>
using namespace std;
int main() {
int bagWeight,n;
cin >> bagWeight >> n;
vector<int> weight(n, 0);
vector<int> value(n, 0);
vector<int> nums(n, 0);
for (int i = 0; i < n; i++) cin >> weight[i];
for (int i = 0; i < n; i++) cin >> value[i];
for (int i = 0; i < n; i++) cin >> nums[i];
for (int i = 0; i < n; i++) {
while (nums[i] > 1) { // 物品数量不是一的,都展开
weight.push_back(weight[i]);
value.push_back(value[i]);
nums[i]--;
}
}
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品,注意此时的物品数量不是n
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}大家去提交之后,发现这个解法超时了,为什么呢,哪里耗时呢?
耗时就在 这段代码:
for (int i = 0; i < n; i++) {
while (nums[i] > 1) { // 物品数量不是一的,都展开
weight.push_back(weight[i]);
value.push_back(value[i]);
nums[i]--;
}
}如果物品数量很多的话,C++中,这种操作十分费时,主要消耗在vector的动态底层扩容上。(其实这里也可以优化,先把 所有物品数量都计算好,一起申请vector的空间。
这里也有另一种实现方式,就是把每种商品遍历的个数放在01背包里面在遍历一遍。
代码如下:(详看注释)
#include<iostream>
#include<vector>
using namespace std;
int main() {
int bagWeight,n;
cin >> bagWeight >> n;
vector<int> weight(n, 0);
vector<int> value(n, 0);
vector<int> nums(n, 0);
for (int i = 0; i < n; i++) cin >> weight[i];
for (int i = 0; i < n; i++) cin >> value[i];
for (int i = 0; i < n; i++) cin >> nums[i];
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < n; i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
// 以上为01背包,然后加一个遍历个数
for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
}
}
}
cout << dp[bagWeight] << endl;
}时间复杂度:O(m × n × k),m:物品种类个数,n背包容量,k单类物品数量
从代码里可以看出是01背包里面在加一个for循环遍历一个每种商品的数量。 和01背包还是如出一辙的。
当然还有那种二进制优化的方法,其实就是把每种物品的数量,打包成一个个独立的包。
和以上在循环遍历上有所不同,因为是分拆为各个包最后可以组成一个完整背包,具体原理我就不做过多解释了,大家了解一下就行,面试的话基本不会考完这个深度了,感兴趣可以自己深入研究一波。
#总结
多重背包在面试中基本不会出现,力扣上也没有对应的题目,大家对多重背包的掌握程度知道它是一种01背包,并能在01背包的基础上写出对应代码就可以了。
至于背包九讲里面还有混合背包,二维费用背包,分组背包等等这些,大家感兴趣可以自己去学习学习,这里也不做介绍了,面试也不会考。
背包问题汇总
年前我们已经把背包问题都讲完了,那么现在我们要对背包问题进行总结一番。
背包问题是动态规划里的非常重要的一部分,所以我把背包问题单独总结一下,等动态规划专题更新完之后,我们还会在整体总结一波动态规划。
关于这几种常见的背包,其关系如下:
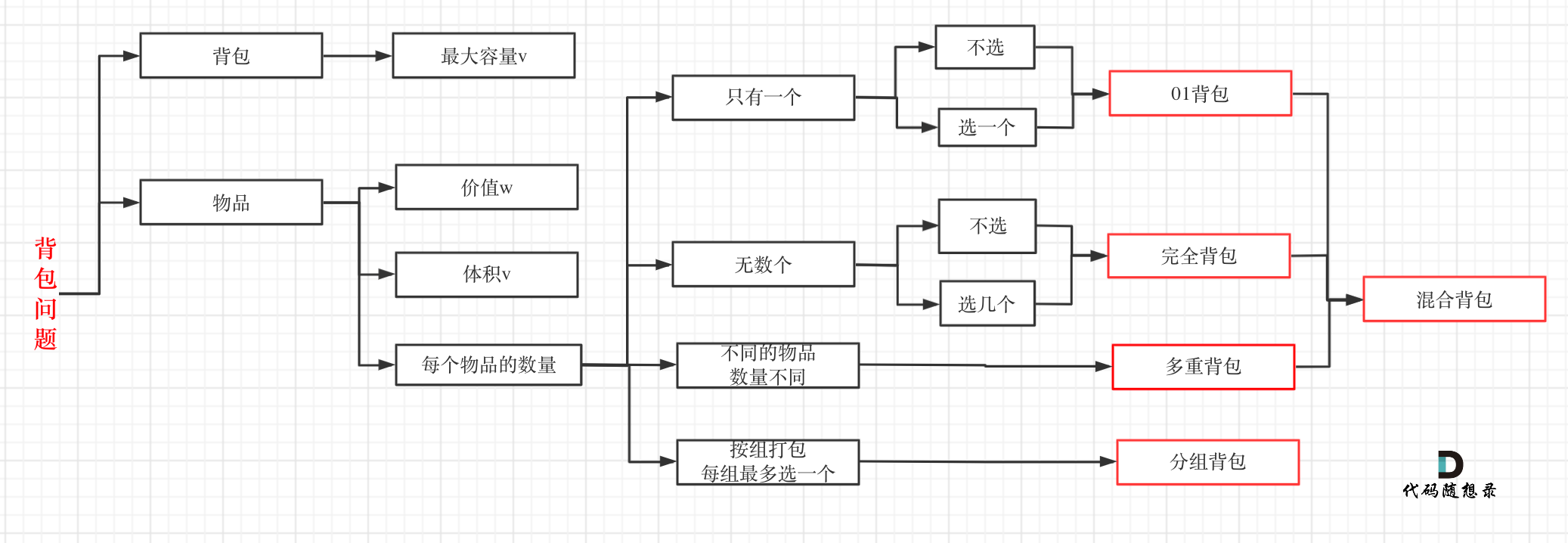
通过这个图,可以很清晰分清这几种常见背包之间的关系。
在讲解背包问题的时候,我们都是按照如下五部来逐步分析,相信大家也体会到,把这五部都搞透了,算是对动规来理解深入了。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
其实这五部里哪一步都很关键,但确定递推公式和确定遍历顺序都具有规律性和代表性,所以下面我从这两点来对背包问题做一做总结。
#背包递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数(opens new window)
#遍历顺序
#01背包
在动态规划:关于01背包问题,你该了解这些!(opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
和动态规划:关于01背包问题,你该了解这些!(滚动数组)(opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
#完全背包
说完01背包,再看看完全背包。
在动态规划:关于完全背包,你该了解这些!(opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ(opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
- 求最小数:动态规划:322. 零钱兑换(opens new window)、动态规划:279.完全平方数(opens new window)
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。
#总结
这篇背包问题总结篇是对背包问题的高度概括,讲最关键的两部:递推公式和遍历顺序,结合力扣上的题目全都抽象出来了。
而且每一个点,我都给出了对应的力扣题目。
最后如果你想了解多重背包,可以看这篇动态规划:关于多重背包,你该了解这些!(opens new window),力扣上还没有多重背包的题目,也不是面试考察的重点。
如果把我本篇总结出来的内容都掌握的话,可以说对背包问题理解的就很深刻了,用来对付面试中的背包问题绰绰有余!
背包问题总结: