目录
题目
原题描述:
题目描述
输入格式
输出格式
输入输出样例
主要思路:
check:
真正的code:
原题描述:
题目描述
C 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 条赛道。
C 城一共有 个路口,这些路口编号为
,有
条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第
条道路连接的两个路口编号为
和
,该道路的长度为
。借助这
条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 ,满足可以从某个路口出发,依次经过 道路
(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 条赛道中长度最小的赛道长度最大(即
条赛道中最短赛道的长度尽可能大)
输入格式
输入文件第一行包含两个由空格分隔的正整数 ,
,分别表示路口数及需要修建的 赛道数。
接下来 行,第
行包含三个正整数
,
,
,表示第
条适合于修建赛道的道 路连接的两个路口编号及道路长度。保证任意两个路口均可通过这
条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出格式
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
输入输出样例
输入 #1
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7输出 #1
31输入 #2
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4输出 #2
15



主要思路:
题目说的很复杂,实际上很简单,就是给你一棵树,然后让你找到m条链,每条链没有公共边,然后问长度最小的链长度最大是多少。
首先,看道这题,先想到二分。
我们可以二分答案,就是最小的链的长度。
接着就是check:
check:
我们可以用个dfs,tmp[x] 就是到x的最大边,则枚举所有到x的边,然后dfs()一下,接着tmp[x] = tmp[it]+边权。
dfs部分代码:
void dfs(int x,int fa,int k)//x是当前节点,k是要达成的长度
{
// cout<<x<<' '<<fa<<' '<<k<<'\n';
tmp[x] = 0;
multiset<int> s;
for(auto it:v[x])
{
if(it.first!=fa)
{
dfs(it.first,x,k);
tmp[x] = tmp[it.first]+it.second;//tmp加上
if(tmp[x]>=k)
{
ans++;//ans是可成立的边数
}
else//否则,就要放进multiset
{
s.insert(tmp[x]);
}
}
}
}这里的multiset就是存储子树内还不够的长度。
接着,我们看一下s里的元素,s非空时,而且s只有一个元素,就说明这个数和谁都不能匹配,那么就要和他的爷爷们连边了(只有一个点可以和爷爷连边)
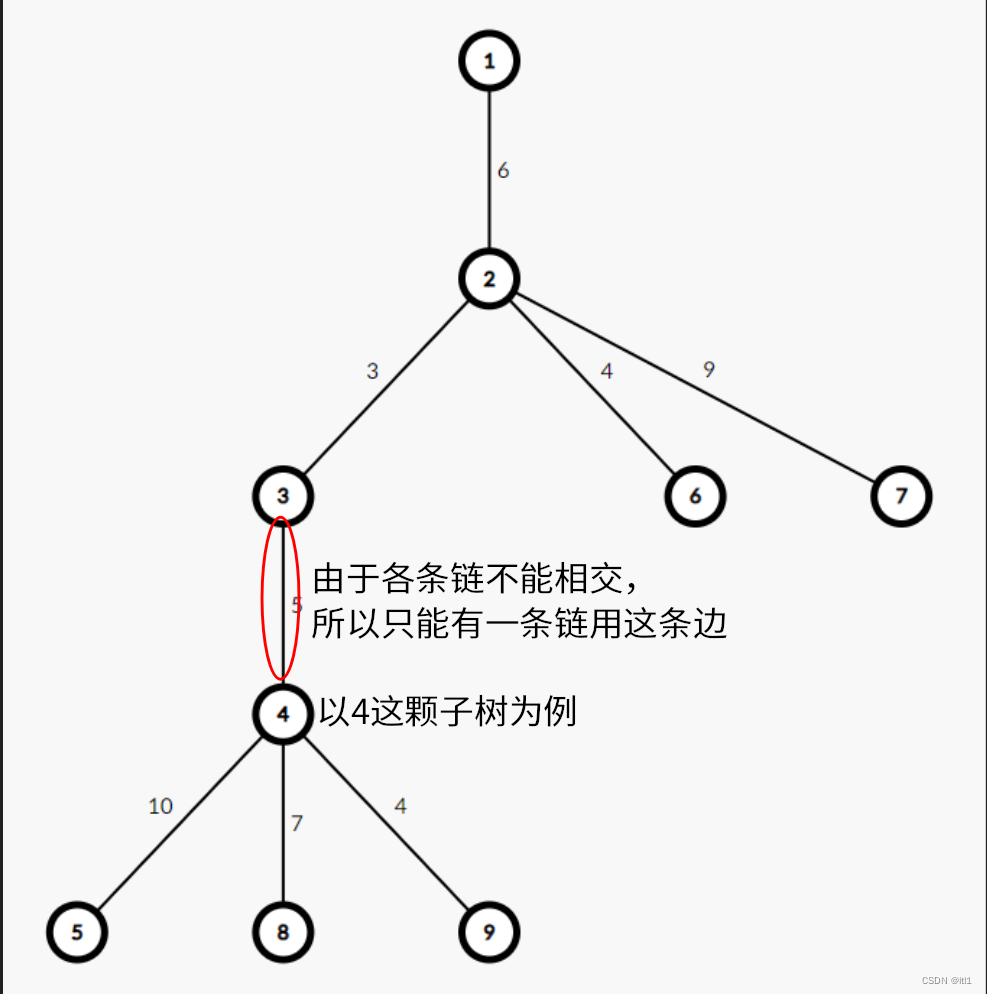
为了给爷爷们减轻负担,所以我们希望让那个点的tmp尽量大(这就是一种贪心)。
否则,就lower_bound(k-s.begin());
我们从小的选大的,为啥呢?

从之前的结论得到,我们要尽量给爷爷们减少麻烦,所以要选大的,所以是小选大
所以最后dfs和check代码长这样
vector<vector<pair<int,int>>>v(500010);
int ans=0;
int tmp[500010];
void dfs(int x,int fa,int k)
{
// cout<<x<<' '<<fa<<' '<<k<<'\n';
tmp[x] = 0;
multiset<int> s;
for(auto it:v[x])
{
if(it.first!=fa)
{
dfs(it.first,x,k);
tmp[x] = tmp[it.first]+it.second;
if(tmp[x]>=k)
{
ans++;
}
else
{
s.insert(tmp[x]);
}
}
}
int mx=0;
while(!s.empty())//贪心思想
{
if(s.size() == 1)
{
tmp[x] = max(mx,*s.begin());
return ;
}
auto it=s.lower_bound(k-*s.begin());
if(it == s.begin()&&s.count(*it) == 1)
{
it++;
}
if(it == s.end())
{
mx = max(mx,*s.begin());
s.erase(s.find(*s.begin()));
}
else
{
ans++;
s.erase(s.find(*s.begin()));
s.erase(s.find(*it));
}
}
tmp[x] = mx;
}
bool check(int mid)
{
ans = 0;
dfs(1,-1,mid);
return ans>=m;
}接着就差不多搞定了。
但还有一个小细节。
就是二分的r他的上限不是自己定义的,而是树的直径。
否则会被这个hack:
2 0
1 2 1000输出:
1000真正的code:
#include<bits/stdc++.h>
using namespace std;
int n,m;
vector<vector<pair<int,int>>>v(500010);
int ans=0;
int tmp[500010];
void dfs(int x,int fa,int k)
{
// cout<<x<<' '<<fa<<' '<<k<<'\n';
tmp[x] = 0;
multiset<int> s;
for(auto it:v[x])
{
if(it.first!=fa)
{
dfs(it.first,x,k);
tmp[x] = tmp[it.first]+it.second;
if(tmp[x]>=k)
{
ans++;
}
else
{
s.insert(tmp[x]);
}
}
}
int mx=0;
while(!s.empty())
{
if(s.size() == 1)
{
tmp[x] = max(mx,*s.begin());
return ;
}
auto it=s.lower_bound(k-*s.begin());
if(it == s.begin()&&s.count(*it) == 1)
{
it++;
}
if(it == s.end())
{
mx = max(mx,*s.begin());
s.erase(s.find(*s.begin()));
}
else
{
ans++;
s.erase(s.find(*s.begin()));
s.erase(s.find(*it));
}
}
tmp[x] = mx;
}
bool check(int mid)
{
ans = 0;
dfs(1,-1,mid);
return ans>=m;
}
int up;
int dfs1(int x,int fa)//数的直径
{
int sum1=0,sum2=0;
for(auto it:v[x])
{
if(it.first == fa)
{
continue;
}
sum2=max(sum2,dfs1(it.first,x)+it.second);
if(sum1<sum2)
{
swap(sum1,sum2);
}
}
up=max(up,sum1+sum2);
return sum1;
}
int main()
{
// freopen("sample (13).in","r",stdin);
ios::sync_with_stdio(0);
cin.tie(0);
cin>>n>>m;
for(int i=1;i<n;i++)
{
int x,y,z;
cin>>x>>y>>z;
v[x].push_back({y,z});
v[y].push_back({x,z});
}
dfs1(1,0);
int l=0,r=up;
int ans=0;
while(l<=r)
{
int mid=(l+r)/2;
if(check(mid))
{
ans = mid;
l = mid+1;
}
else
{
r = mid-1;
}
}
cout<<ans;
return 0;
}