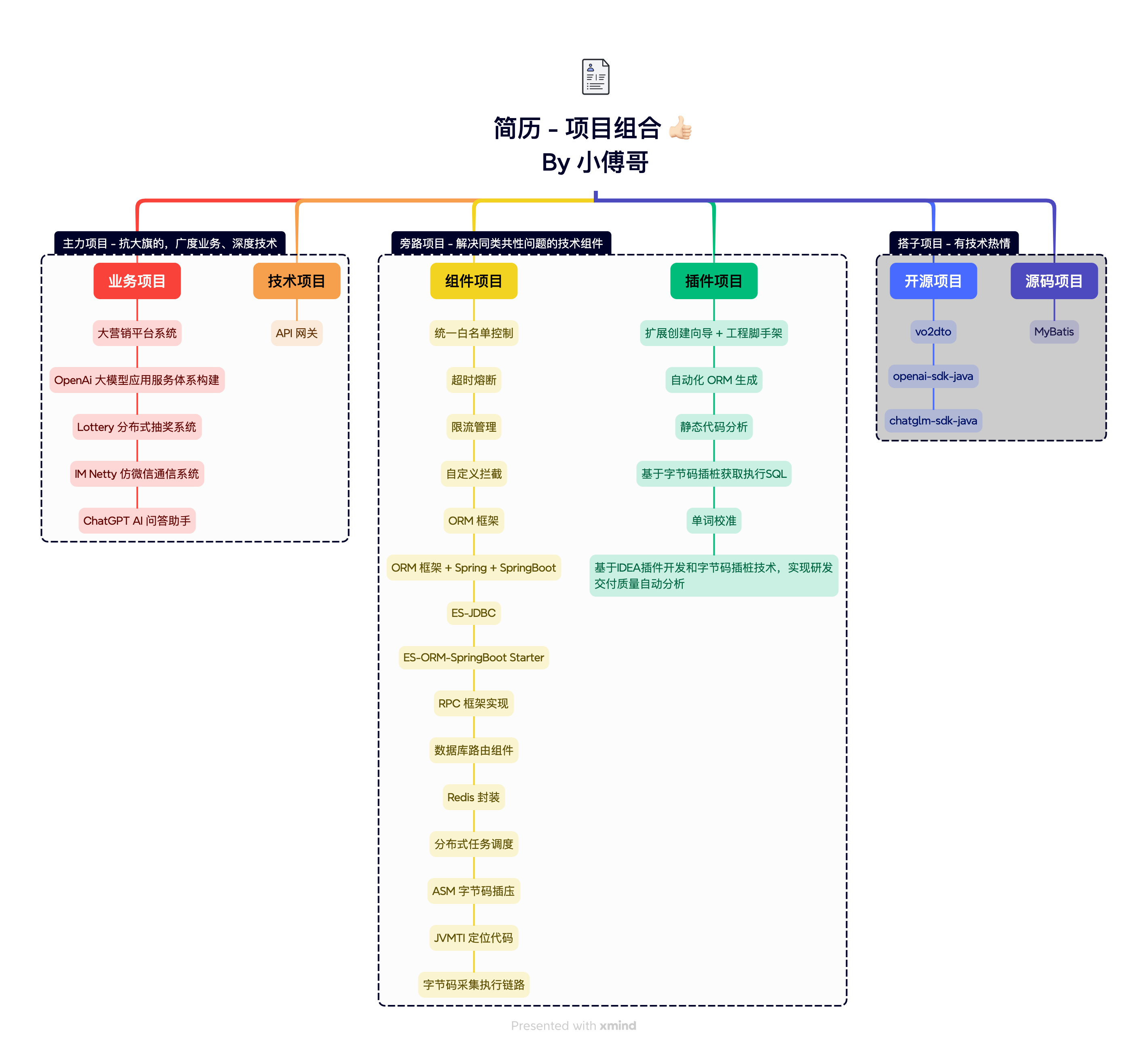
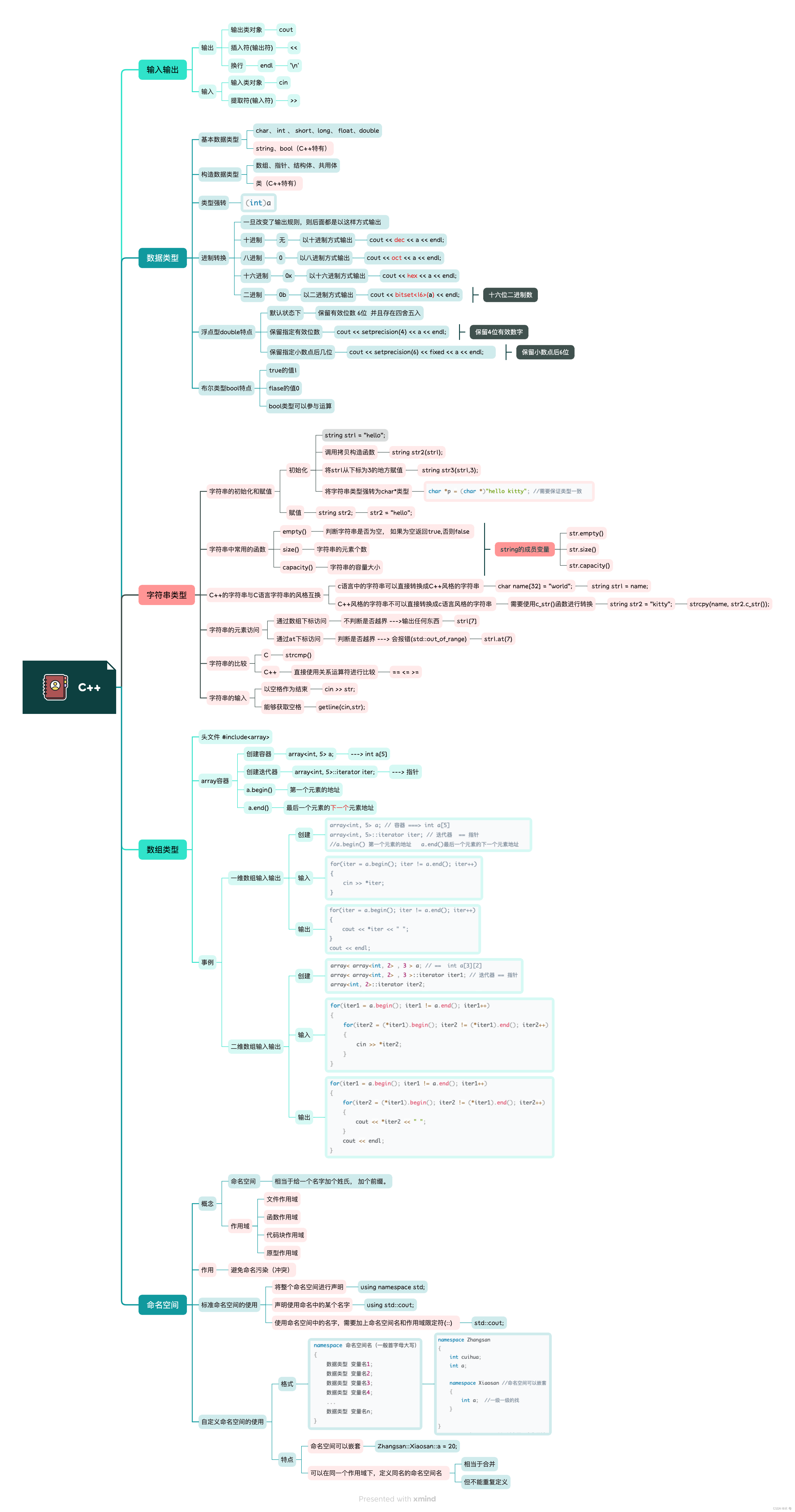
来源:《OpenCV3编程入门》,怀念毛星云大佬🕯️
说明:本系列重点关注各种图像处理算法的原理、作用和对比
形态学滤波(1 ):腐蚀与膨胀
形态学槪述
数学形态学的概念:
数学形态学(Mathematical morphology)是立在格论和拓扑学基础之上的图像分析学科,足数学形态学阁像处现的基本理论。其基本的运算包括:二值腐蚀和膨胀、二值开闭运算、骨架抽収、极限腐蚀、击中击不中变换、形态学梯度、Top-hat变换、颗粒分析、流域变换、灰值腐蚀和膨胀、灰值开闭运算、灰值形态学梯度等。简中来讲,形态学操作就是基于形状的一系列图像处理操作。OpenCV为进行图像的形态学变换提供了快捷、方便的函数。最基本的形态学操作有两种,分别是:膨胀(dilate)与腐蚀(erode)。膨胀与腐蚀能实现多种多样的功能,主要如下。
- 消除噪声;
- 分割(isolate)出独立的阁像元索,在图像中连接(join)相邻的元素:
- 寻找图像中的明显的极大值K域或极小值区域;
- 求出图像的梯度。
在进行腐蚀和膨胀的讲解之前,首先提醒大家注意.腐蚀和膨胀是对**白色部分(高亮部分)**而言的,不是黑色部分。膨胀是图像中的髙亮部分进行膨胀,类似于“领域扩张”,效果图拥有比原图更大的高亮区域;腐蚀是原图中的髙亮部分被腐蚀,类似于“领域被蚕食效果图拥有比原图更小的高亮区域。
例图:
膨胀
膨胀(dilate)就是求局部最大值的操作。从数学角度来说,膨胀或者腐蚀操作就是将图像(或图像的一部分区域,称之为A)与核(称之为B)进行卷积。核可以是任何形状和大小,它拥有一个单独定义出来的参考点,我们称其为锚点(anchorpoint)。多数情况下,核是一个小的,中间带有参考点和实心正方形或者圆盘。其实,可以把核视为模板或者掩码。而膨胀就是求局部最大位的操作。核B与图形卷积,即计算核B覆盖的区域的像素点的最大值,并把这个最大值赋值给参考点指定的像素。这样就会使图像中的高亮区域逐渐増长,这就是膨账操作的初衷。
示例图:
腐蚀
膨胀和腐蚀 ( erode) 是相反的一对操作 ,所以腐蚀就是求局部最小值的操作。我们一般都会把腐蚀和膨胀进行对比理解和学习。两者的
函数原型也是基本一样的。
示例图:
形态学滤波(2):开运算、闭运算、形态学梯度、顶帽、黑帽
形态学的高级形态,往往都是建立在腐蚀和膨胀这两个基本操作之上的。
开运算
开运算(Opening Operation),其实就是先腐蚀后膨胀的过程。开运算可以用来消除小物体,在纤细点处分离物体,并且在平滑较大物体的边界的同时不明显改变其面积。
示例图:
闭运算
先膨账后腐蚀的过程称为闭运算(Closing Operation),闭运算能够排除小型黑洞(黑色区域)。
示例图:
形态学梯度
形态学梯度(Morphological Gradient)是膨胀图与腐蚀图之差。对二值图像进行这操作可以将团块(blob)的边缘突出出来。我们可以用形态学梯度来保留物体的边缘轮廓。
个人理解(以黑白2值图为例):膨胀和腐蚀都是对边缘进行操作,腐蚀是黑色向白色区域内腐蚀,膨胀是白色向黑色区域内膨胀,向内和向外的操作会产生一个粗的线条区域,这个区域在腐蚀的时候是黑色,在膨胀的时候是白色,这个时候差值就是白色,其他的区域在腐蚀和膨胀的时候是不变的,差值就是0,也就是黑色,这样白色区域就表现出了边缘信息。
示例图:
顶帽
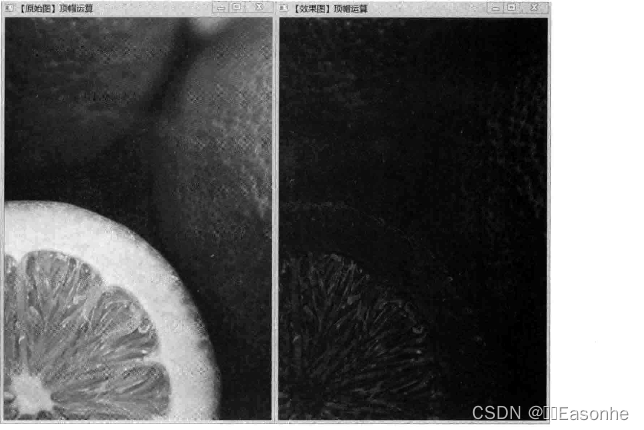
顶帽运算(Top Hat)又常常被译为"礼帽“运算,是原图像与开运算的结果图之差,因为开运算带来的结果是放大了裂缝或者局部低亮度的区域。由此,从原图中减去开运算后的图,得到的效果图突出了比原图轮廓周围的区域更明亮的区域,且这一操作与选择的核的大小相关。顶帽运算往往用来分离比邻近点亮一些的斑块。在一幅图像具有大幅的背景,而微小物品比较有规律的情况下,可以使用顶帽运算进行背景提取。
示例图:
黑帽
黑帽(Black Hat)运算是闭运算的结果图与原图像之差,黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域,且这一操作
和选择的核的大小相关。所以,黑帽运算用來分离比邻近点暗一些的斑块,效果图有着非常完美的轮廓。示例如阁6.38和图6.39所示。