2023年第三届中国高校大数据挑战赛第二场赛题D题赛题：行业职业技术培训能力评价（成品论文代码与思路视频讲解）

赛题

中国是制造业大国，产业门类齐全，每年需要培养大量的技能娴熟的技术工人进入工厂。某行业在全国有多所不同类型（如国家级、省级等）的职业技术培训学校，进行 5 种技能培训。学员入校时需要进行统一的技能考核（称作“入校考核”），培训结束后再次进行统一考核（称作“离校考核”）并根据该考核成绩总分位次颁发级别不等的职业技术资格证和工作推荐。与此同时，行业主管部门还需要根据考核成绩对培训学校的培训效果进行评价。

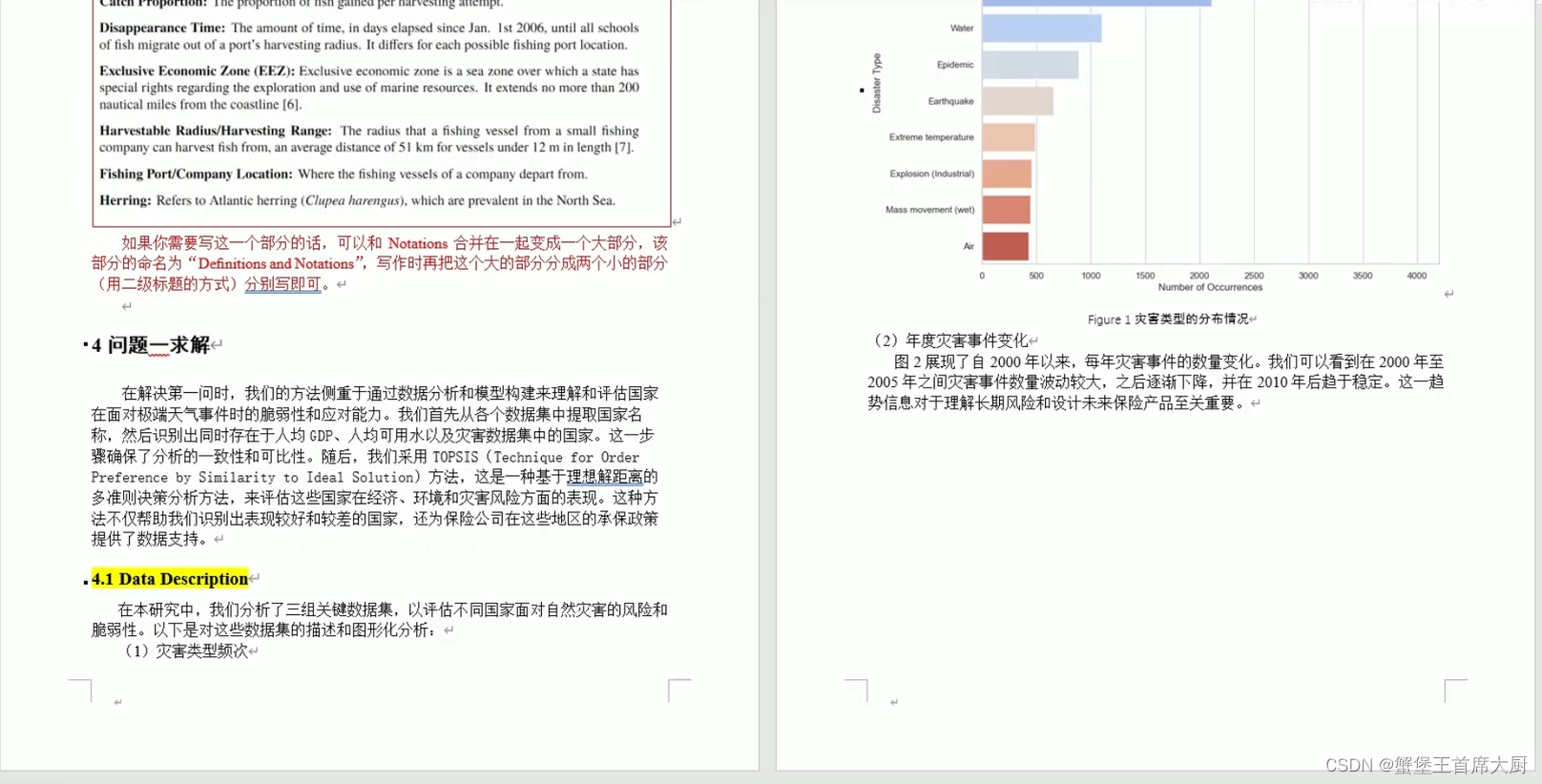
长期以来，该行业主管部门都是以学员离校考核成绩来评价培训学校的培训能力。这种评价制度显然有瑕疵，因为学员最终的考核成绩不仅仅是由于培训学校的培训能力导致的，还有学员的素质等其他因素，这使得部分培训学校不是把主要精力放在技能培训方法方式的改进上面，而是去抓生源质量。这样会最终加剧培训效果的不均衡，并会挫伤大多数培训学校和培训教员的工作积极性，影响了学校改进培训教学管理的积极性，导致总体培训质量下降。因此，在对不同类型的培训学校进行公正合理的培训能力评价是一件很有意义的事情。附件数据给出了 6 个类型、160 个培训学校 32165 个学员的入学、离校的 5 种技能考核和总分成绩。为了便于比较和研究，所有数据已经进行数据标准化。

请你查阅相关文献，改造或独创性的运用大数据科学与技术方法，解决以下问题。

般而言，入学的各技能考核成绩与对应的离校考核成绩绩可能存在着或多或少或无的关联性。请你对此进行分析。
不同的培训学校有不同的生源质量、学校办学条件、学校师资水平等的差异，仅仅用离校考核成绩的高低无法真正有效的体现一个学校的真正的培训能力。请你运用附件数据，阐明什么类型的培训学校，具体哪些培训学校在培训能力上面有较高的水平？请给不同类型的培训学校培训能力进行排序，以及给出培训能力前 10 的学校编号。
每个培训学校有不同的特色，如有些培训学校技能 1 的培训能力很好，而有些学校可能是技能 2 的培训能力上有优势。请问，哪些培训学校分别在哪种技能培训能力上有特色？每种技能列出前 5 名的学校编号。4.

4.假设行业主管部门计划给 10000 名学员颁发职业资格证书。请问，哪些因素对获取职业资格证书有着非常重要的影响？数据表中最后有 10 名学员的离校考核成绩被删除，请你判断他们能否获取职业资格证？如果职业资格证分为一级和二级（一、二级比例为 1:3），那这 10 名学员中谁能获取一级职业资格证书？

问题分析

问题 1 分析：使用相关性分析（如皮尔逊或斯皮尔曼相关系数）来建立入学和离校考核成绩之间的关系。
问题 2 分析：使用boost模型构建一个模型来衡量学校的培训效果，控制学员入学时的技能水平。
问题 3 分析：对于每个技能，使用问题 2 的方法分别评估学校的表现，识别每种技能培训能力最强的学校。
问题 4 分析：利用随机森林模型来预测学员是否能获得职业资格证书，以及其等级。

python代码

# 导入数据
file_path = '赛题数据.xlsx'

try:
    data_xlsx = pd.ExcelFile(file_path)
    
    sheet_names = data_xlsx.sheet_names
    
    data_preview = pd.read_excel(data_xlsx, sheet_name=sheet_names[0], nrows=5)
    
    (sheet_names, data_preview)
except Exception as e:
    str(e)
sheets_data = {}
for sheet_name in sheet_names:
    try:
        sheets_data[sheet_name] = pd.read_excel(data_xlsx, sheet_name=sheet_name, nrows=5)
    except Exception as e:
        sheets_data[sheet_name] = str(e)

sheets_data.keys(), {sheet_name: sheets_data[sheet_name].head() for sheet_name in sheets_data.keys()}

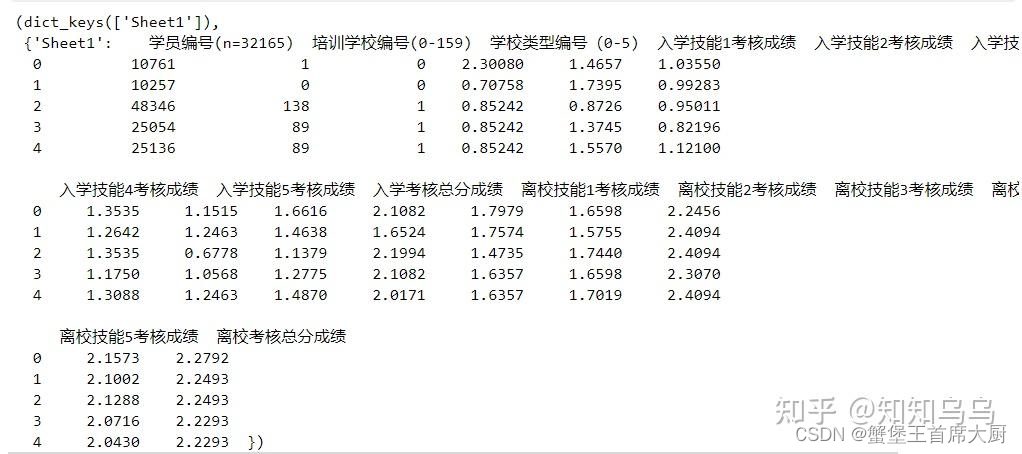
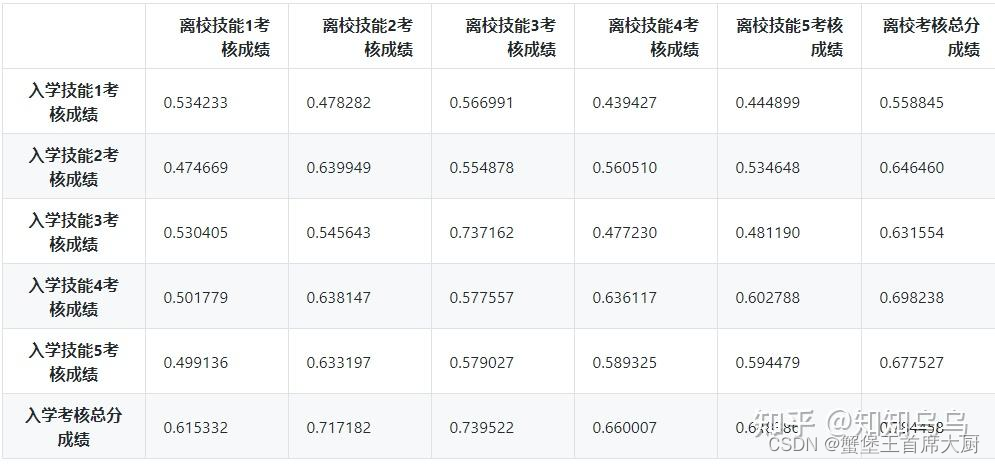
在这里插入图片描述

#皮尔逊相关性计算
data = pd.read_excel(data_xlsx, sheet_name='Sheet1')


correlations = data[['入学技能1考核成绩', '入学技能2考核成绩', '入学技能3考核成绩', '入学技能4考核成绩', '入学技能5考核成绩', '入学考核总分成绩',
                     '离校技能1考核成绩', '离校技能2考核成绩', '离校技能3考核成绩', '离校技能4考核成绩', '离校技能5考核成绩', '离校考核总分成绩']].corr()


correlations_select = correlations.loc[['入学技能1考核成绩', '入学技能2考核成绩', '入学技能3考核成绩', '入学技能4考核成绩', '入学技能5考核成绩', '入学考核总分成绩'],
                                       ['离校技能1考核成绩', '离校技能2考核成绩', '离校技能3考核成绩', '离校技能4考核成绩', '离校技能5考核成绩', '离校考核总分成绩']]


correlations_select

在这里插入图片描述

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 选择特征和标签
X = data[['入学技能1考核成绩', '入学技能2考核成绩', '入学技能3考核成绩', '入学技能4考核成绩', '入学技能5考核成绩']]
y = data['离校考核总分成绩']

# 标准化特征数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 分割数据集为训练集和测试集，测试集大小设置为20%
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

X_train.shape, X_test.shape, y_train.shape, y_test.shape

在这里插入图片描述

from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 填充目标变量中的缺失值
y_filled = data['离校考核总分成绩'].fillna(data['离校考核总分成绩'].median())

# 选择特征和已填充缺失值的目标变量
X = data[['入学技能1考核成绩', '入学技能2考核成绩', '入学技能3考核成绩', '入学技能4考核成绩', '入学技能5考核成绩']]
y = y_filled

# 标准化特征数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 分割数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)

# 训练梯度提升回归模型
gbrt = GradientBoostingRegressor(n_estimators=200, learning_rate=0.01, max_depth=6, random_state=42)
gbrt.fit(X_train, y_train)

# 进行预测
y_pred_train = gbrt.predict(X_train)
y_pred_test = gbrt.predict(X_test)

# 计算训练集和测试集的均方误差
mse_train = mean_squared_error(y_train, y_pred_train)
mse_test = mean_squared_error(y_test, y_pred_test)

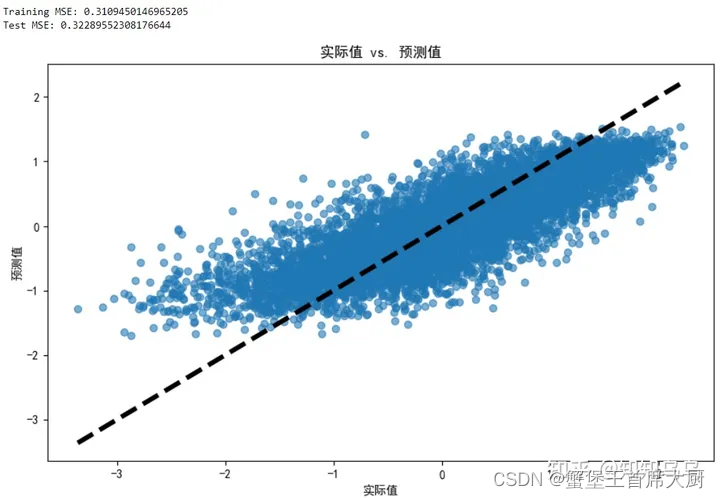
print(f"Training MSE: {mse_train}")
print(f"Test MSE: {mse_test}")

# 绘制实际值与预测值的比较图
plt.figure(figsize=(10, 6))
plt.scatter(y_test, y_pred_test, alpha=0.6)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4)
plt.title('实际值 vs. 预测值')
plt.xlabel('实际值')
plt.ylabel('预测值')
plt.show()

在这里插入图片描述

import matplotlib.pyplot as plt

feature_importances = rfc.feature_importances_
features = X.columns

# 排序特征重要性
sorted_idx = np.argsort(feature_importances)[::-1]

plt.figure(figsize=(10, 6))
plt.title("特征重要性")
plt.bar(range(X.shape[1]), feature_importances[sorted_idx], align="center")
plt.xticks(range(X.shape[1]), features[sorted_idx], rotation=45)
plt.xlim([-1, X.shape[1]])
plt.show()

from sklearn.metrics import confusion_matrix
import seaborn as sns

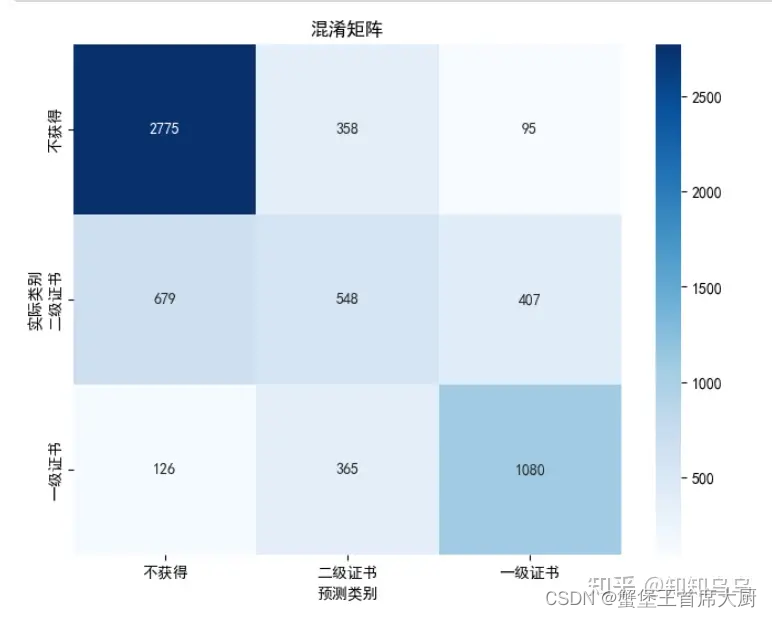
# 计算混淆矩阵
cm = confusion_matrix(y_test, y_pred)

plt.figure(figsize=(8, 6))
sns.heatmap(cm, annot=True, fmt="d", cmap="Blues", xticklabels=['不获得', '二级证书', '一级证书'], yticklabels=['不获得', '二级证书', '一级证书'])
plt.ylabel('实际类别')
plt.xlabel('预测类别')
plt.title('混淆矩阵')
plt.show()

在这里插入图片描述

from sklearn.metrics import classification_report

report = classification_report(y_test, y_pred, target_names=['不获得', '二级证书', '一级证书'])
print(report)

在这里插入图片描述

B站附上详细视频讲解

在这里插入图片描述

完整论文限量销售（限量销售，足够一二等奖）

在这里插入图片描述