二叉树使用递归，就要想使用前中后哪种遍历方式？

本题使用哪种遍历都是可以的！

我们下面以前序遍历为例。

那么我们来按照递归三部曲来解决：

1. 确定递归函数的参数和返回值：

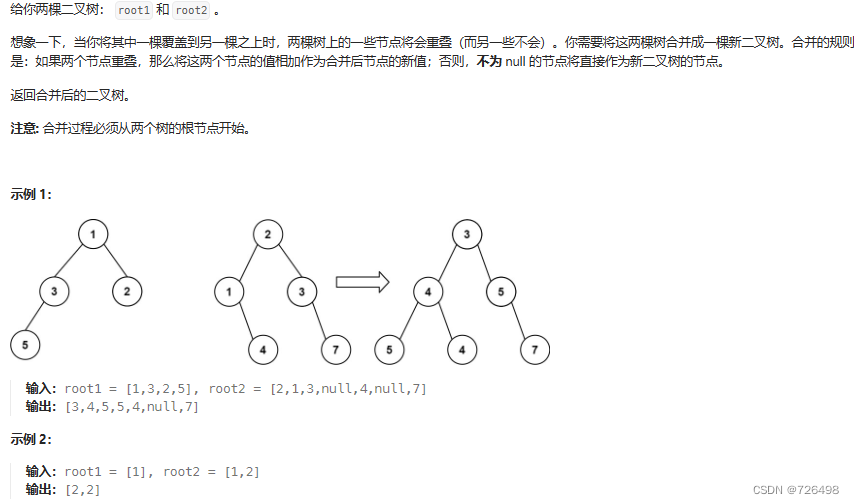
首先要合入两个二叉树，那么参数至少是要传入两个二叉树的根节点，返回值就是合并之后二叉树的根节点。

public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {

1. 确定终止条件：

因为是传入了两个树，那么就有两个树遍历的节点root1 和 root2，如果root1 == NULL 了，两个树合并就应该是 root2 了（如果root2也为NULL也无所谓，合并之后就是NULL）。

反过来如果root2 == NULL，那么两个数合并就是root1（如果root1也为NULL也无所谓，合并之后就是NULL）。

代码如下：

if (root1 == NULL) return root2; // 如果root1为空，合并之后就应该是root2
if (root2 == NULL) return root1; // 如果root2为空，合并之后就应该是root1

1. 确定单层递归的逻辑：

单层递归的逻辑就比较好写了，这里我们重复利用一下root1这个树，root1就是合并之后树的根节点（就是修改了原来树的结构）。

那么单层递归中，就要把两棵树的元素加到一起。

root1.val=root1.val+root2.val;

接下来root1 的左子树是：合并roo t1左子树roo t2左子树之后的左子树。

root1 的右子树：是 合并roo t1右子树roo t2右子树之后的右子树。

最终root1就是合并之后的根节点。

代码如下：

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null) return root2;
        if(root2 == null) return root1;
        root1.val=root1.val+root2.val;
        root1.left=mergeTrees(root1.left,root2.left);
        root1.right=mergeTrees(root1.right,root2.right);
        return root1;
    }
}