一维前缀和

适用场景

• 求一段区间的和。

比如有一个数列 ：

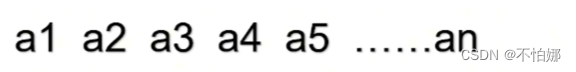
如果我们要求 [l,r]即某个区间内的数组和的时候，思路就是每遍历一个元素就进行求和，记录下加到al时的和值以及加到ar时的和值，两个值相减就得到区间和了。

这时求一次和的情况，时间复杂度是O(n)，那如果要进行多次区间求和，每次都要进行一次这样的操作，那么n次的时间复杂度就是O(n * n)。

为了避免出现上面的情况，我们以空间换时间，在每次进行求和的时候将和值记录下来，也就是说我们会另外构造一个数组，这个数组就是前缀和数组。这样我们只需遍历一次数组，在需要求区间和的时候直接从前缀和数组中取出相应的值进行减法就可以了。

示例

java参考代码：

package org.example;

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); //序列长度
        int m = sc.nextInt(); //询问次数
        int[] nums = new int[n]; //序列数组
        int[] sums = new int[n]; //前缀和数组
        //构造序列数组的同时构造前缀和数组
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
            //构造前缀和数组
            if (i == 0) {
                sums[i] = nums[i];
            } else {
                sums[i] = sums[i - 1] + nums[i];
            }
        }
        while ( m-- > 0) {
            int l = sc.nextInt();
            int r = sc.nextInt();
            System.out.println("区间和：" + (sums[r] - sums[l]));
        }
    }
}

二维前缀和

适用场景

• 求一个矩阵中任意子矩阵的数之和

---

一种情况

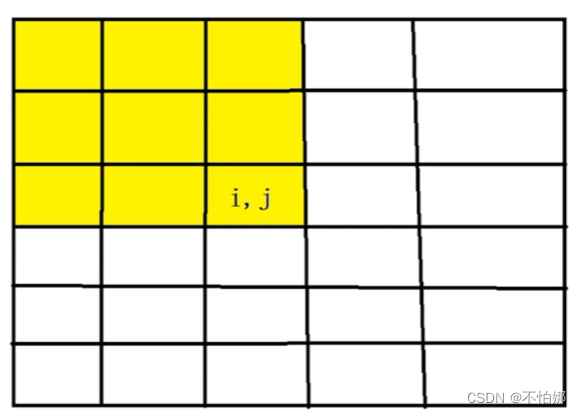
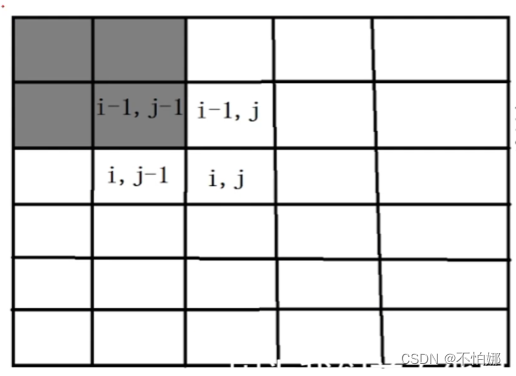
如果要求一个i*j（i行j列）的子矩阵的数之和，如图：

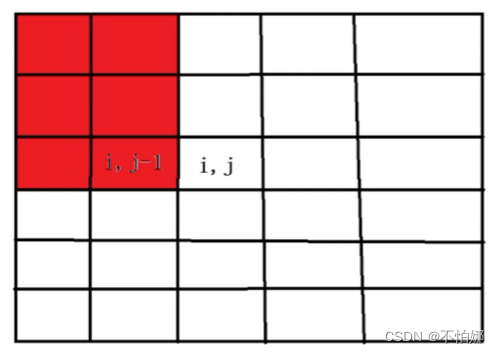
1. 先求i * (j - 1)子矩阵的数之和，如图：
   
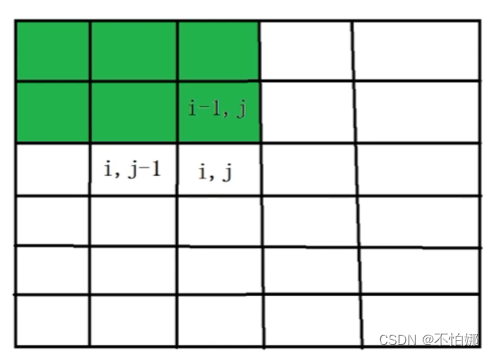
2. 再求（i - 1) * j 子矩阵的数之和，如图：
   
3. 将以上两值相加后再加上第i行第j列那个元素
4. 最后一步去重，如图，灰色区域在前面两步加了两次，所以减去，重复的部分是(i - 1) * (j - 1)子矩阵
   
   最后的公式就是：
   

---

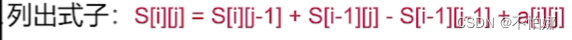
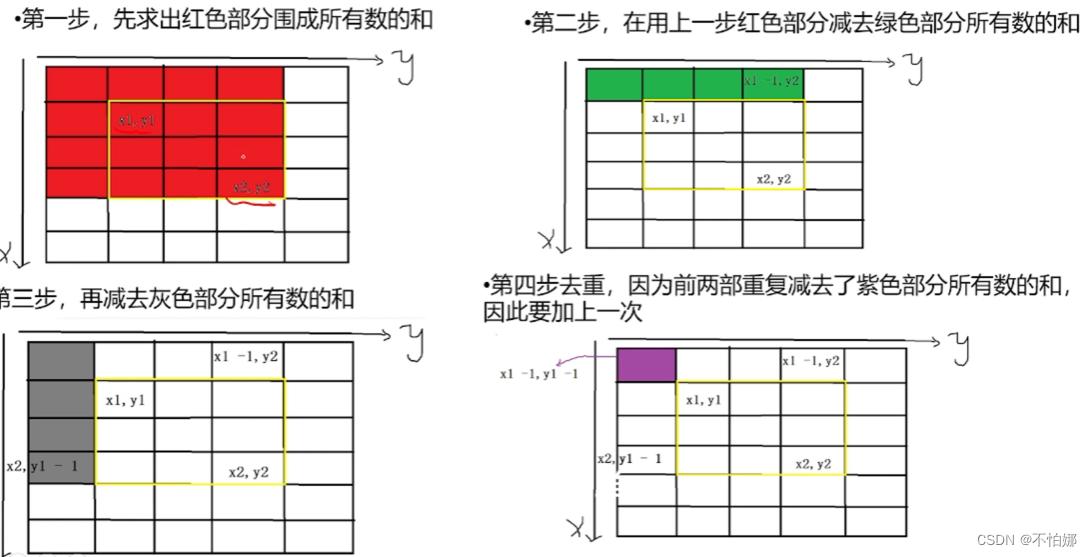
另一种情况

我们要求的子矩阵是中间的，如下图，我们要求黄色框子矩阵的数之和：
和前面的思路差不多。上面是要去重，下面这种情况则需要加上重复删除的部分。

示例

java参考代码：

package org.example;

import javax.sound.midi.Soundbank;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); //n行
        int m = sc.nextInt(); //m列
        int q = sc.nextInt(); //询问q次
        int[][] a = new int[n + 1][m + 1];  //构造矩阵
        int[][] s = new int[n + 1][m + 1];  //构造二维前缀和
        //构造矩阵和二维前缀和
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                a[i][j] = sc.nextInt();
                s[i][j] = s[i - 1][j] + s[i][j - 1] + a[i][j] - s[i - 1][j - 1];
            }
        }
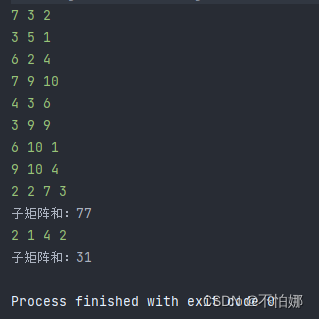
        while (q-- > 0) {
            int x1 = sc.nextInt();
            int y1 = sc.nextInt();
            int x2 = sc.nextInt();
            int y2 = sc.nextInt();
            System.out.println("子矩阵和：" + (s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]));
        }
    }
}