问题描述

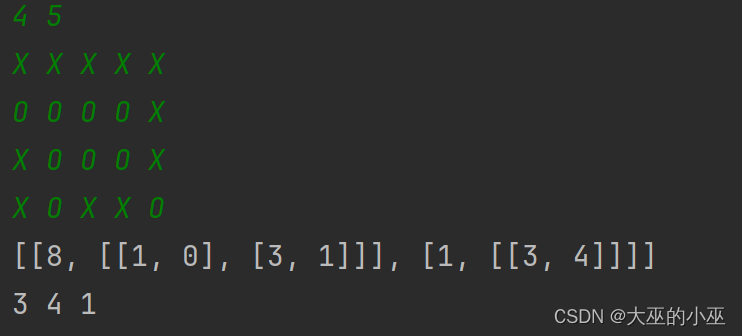
找到最大的单入口空闲区域。
空闲区域是由连通的’O’组成的区域，位于边界的’O’可以是入口，
单入口空闲区域即有且只有一个位于边界的’O’作为入口的由连通的’O’组成的区域。
如果两个元素在水平或垂直方向相邻，则称它们是“连通”的。

输入输出

输入：

1. 第一行：m n
   行数m，列数n，以空格分隔，1<=m,n<=200。
2. 剩余各行是矩阵各行元素，元素为‘X’或‘O’，各元素间以空格分隔

输出：

1. 若有唯一符合要求的区域，输出入口坐标i，j和区域大小size，以空格分隔：i j size
2. 若有多个符合要求的区域，输出符合要求的区域个数
3. 若没有符合要求的区域，输出NULL

代码实现

def rec(i, j, ans):
    """给定i,j，返回该位置区域中的所有O的个数，将入口坐标放在ans中"""
    # 上下左右四个方向，如果周围元素为 被遍历过的元素或为X的元素，就是终止条件
    # 终止条件：周围没有 未被遍历并且为O的元素
    count = 0
    flag = [martrix[i + x][j + y] for x, y in directions if
            0 <= i + x < m and 0 <= j + y < n and not marked[i + x][j + y] and martrix[i + x][j + y] == 'O']
    if not flag:
        return count
    for x, y in directions:
        nxt_i, nxt_j = i + x, j + y
        if 0 <= nxt_i < m and 0 <= nxt_j < n and not marked[nxt_i][nxt_j] and martrix[nxt_i][nxt_j] == 'O':
            marked[nxt_i][nxt_j] = True
            if 0 == nxt_i or nxt_i == m - 1 or 0 == nxt_j or nxt_j == n - 1:# 位于边界上
                ans.append([nxt_i, nxt_j])
            count += 1 + rec(nxt_i, nxt_j, ans)

    return count


m, n = list(map(int, input().split(' ')))
martrix = [input().split(' ') for _ in range(m)]
marked = [[False] * n for _ in range(m)]  # 是O并且被遍历过的元素为True
directions = [(-1, 0), (0, -1), (1, 0), (0, 1)] # 上下左右四个方向


# 测试递归rec函数
# i, j = 1, 1
# marked[i][j] = True
# ans = []
# print(rec(1, 1, ans))
# print(ans)
# print(marked)

res = []  # 存储空闲区域，记录大小和所有区域入口
for i in range(m):
    for j in range(n):
        if not marked[i][j] and martrix[i][j] == 'O':
            marked[i][j] = True
            ans = []
            if 0 == i or i == m - 1 or 0 == j or j == n - 1:# 位于边界上
                ans.append([i, j])
            count = 1 + rec(i, j, ans)
            res.append([count, ans])

print(res)
# 过滤掉大于1 的入口
res = [[r[0], r[1][0][0], r[1][0][1]] for r in res if len(r[1]) == 1]
if len(res) == 0:
    print('NULL')
else:
    res.sort(key=lambda x: -x[0])  # 按照区域大小降序排列
    res = [r for r in res if r[0] == res[0][0]]
    if len(res) == 1:
        data = res[0]
        print(f'{data[1]} {data[2]} {data[0]}')
    else:
        print(len(res))