1.斐波那契数列的时间复杂度问题


每一行分别是2^0---2^1---2^2-----2^3-------------------------------------------2^(n-2)

利用错位相减法,可以得到结果是,2^(n-1)-1,其实还是要减去右下角的灰色部分,我们可以拿简单的数字进行举例子,右下角会先变为2,1;例如
5
4 3
3 2 2 1
2 1
这个例子就可以看出来:左下角还有数据的时候,右下角就已经可以得出结果了,但是随着n的增加,这个右下角的影响对整体越来越小,所以我们可以忽略,我们只需要关注计算次数的数量级,所以,斐波那契数列的复杂度就是2^n;
2.空间复杂度
算法运行占用的额外的空间的一种量度
系统自己开辟的空间不属于空间复杂度的范畴,我们自己开辟的空间才属于空间复杂度
斐波那契数列的空间复杂度是O(N),递归开辟函数栈帧,回调的时候函数栈帧继续利用以后才会销毁,但是这个过程时间是累积的;所以时间累加,空间重复利用;
所以:时间是一去不复返的,空间是可以重复利用的;
3.函数栈帧的进一步理解

栈帧的销毁是归还使用权,还给了操作系统,并不是真正的销毁,main函数开辟函数栈帧,调用func1函数以后开辟新的栈帧,使用完之后栈帧销毁,func2开辟的还是func1的这块空间,所以打印的地址一样;归还栈帧以后其他的函数还是可以使用的;
这个时候,再来看看斐波那契数列,他调用的过程是return fib(n-1)+fib(n-2),他会先调用左边的n-1,,接着调用下一个n-1,他在调用完成以后,回调剩下的n-2的时候和原来使用的栈帧地址是一样的,这样就减少了空间复杂度,开辟的空间最后都会销毁,空间复杂度计算的是占用空间最多时候的情况;
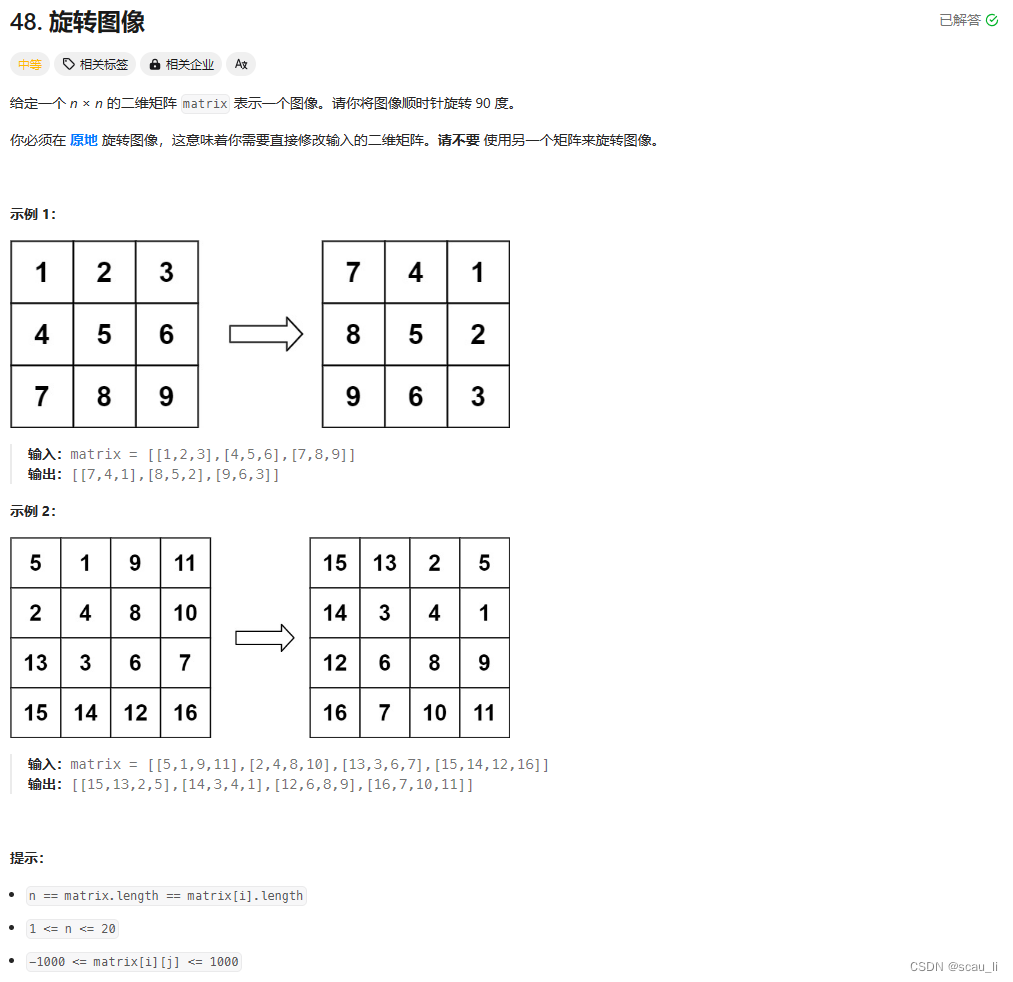
4.轮转数组带你认识复杂度

(1)我们可以使用3次逆置的做法

这个做法的时间复杂度是O(N),空间复杂度是O(1);关键是对于节点处的数据下标的控制,先让左边
逆置,再让右边逆置,最后整体进行倒序;
(2)调用库函数memcpy
这个做法就是拿空间换时间,需要多开辟数组空间,这个里面的时间,空间复杂度都是O(N);