例解变分自编码器（VAE）

news2024/11/16 13:37:47

本文通过一个回归例子介绍变分自编码器。产生训练和测试样本的代码如下：

# data
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def f(x, sigma):
    # y = 10 * sin(2 * pi) + epsilon
    return 10 * np.sin(2 * np.pi * (x)) + np.random.randn(*x.shape) * sigma

num_of_samples = 64 # 样本数
noise = 1.0 # 噪音规模


X = np.linspace(-0.5, 0.5, num_of_samples).reshape(-1, 1)
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_label = f(X, sigma=noise) # 样本的label
y_truth = f(X, sigma=0.0) # 样本的真实值

plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X, y_truth, label='Ground Truth')
plt.title('Noisy training data and ground truth')
plt.legend();

训练和测试样本来自正弦函数，并加入了高斯噪音：
请添加图片描述

首先采用简单的浅层神经网络模型：

class BaseModel():
    def __init__(self):
        self.w_0 = tf.Variable(tf.random.truncated_normal([1, 8], mean=0., stddev=1.))
        self.b_0 = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.w_1 = tf.Variable(tf.random.truncated_normal([8, 8], mean=0., stddev=1.))
        self.b_1 = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.w_2 = tf.Variable(tf.random.truncated_normal([8, 1], mean=0., stddev=1.))
        self.b_2 = tf.Variable(tf.random.truncated_normal([1], mean=0., stddev=1.))
    
    def forward(self, x):
        x = tf.cast(x, tf.float32)
        h = tf.math.sigmoid(tf.matmul(x, self.w_0) + self.b_0)
        h = tf.math.sigmoid(tf.matmul(h, self.w_1) + self.b_1)
        y = tf.matmul(h, self.w_2) + self.b_2
        return y
    
    def train_predict(self, x, label, x_test):     
        y = self.forward(x)
        y_test = self.forward(x_test)
        
        loss = tf.losses.mean_squared_error(y, label)
        optimizer = tf.train.GradientDescentOptimizer(0.01, name="opt")
        gradient = optimizer.compute_gradients(loss)
        opt = optimizer.apply_gradients(gradient)
        init = tf.global_variables_initializer()
        with tf.Session() as sess:
            sess.run(init)
            train_batch = 0
            while train_batch < 100000:
                sess.run(opt)
                if train_batch%1000 == 0:
                    print("train_batch : %s" % train_batch)
                    print(loss.eval())
                train_batch += 1
            
            predict = y_test.eval()
        return predict

model = BaseModel()
y_test = model.train_predict(X, y_label, X_test)
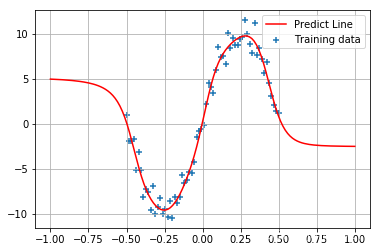
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, y_test, 'r-', label='Predict Line')
plt.grid()
plt.legend()

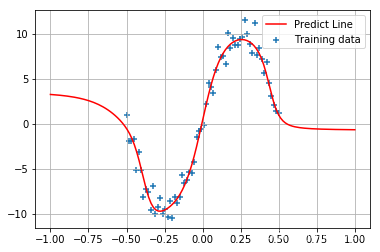
请添加图片描述

将训练目标改为最大似然目标：



class BaseModelV2():
    def __init__(self):
        self.w_0 = tf.Variable(tf.random.truncated_normal([1, 8], mean=0., stddev=1.))
        self.b_0 = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.w_1 = tf.Variable(tf.random.truncated_normal([8, 8], mean=0., stddev=1.))
        self.b_1 = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.w_2 = tf.Variable(tf.random.truncated_normal([8, 1], mean=0., stddev=1.))
        self.b_2 = tf.Variable(tf.random.truncated_normal([1], mean=0., stddev=1.))
    
    def forward(self, x):
        x = tf.cast(x, tf.float32)
        h = tf.math.sigmoid(tf.matmul(x, self.w_0) + self.b_0)
        h = tf.math.sigmoid(tf.matmul(h, self.w_1) + self.b_1)
        y = tf.matmul(h, self.w_2) + self.b_2
        return y
    
    def gaussian_pdf(self, x, mu, sigma):
        return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)

    def train_predict(self, x, label, x_test):     
        y = self.forward(x)
        y_test = self.forward(x_test)
        
        loss = -tf.reduce_sum(self.gaussian_pdf(label, y, 1.0))
        optimizer = tf.train.GradientDescentOptimizer(0.01, name="opt")
        gradient = optimizer.compute_gradients(loss)
        opt = optimizer.apply_gradients(gradient)
        init = tf.global_variables_initializer()
        with tf.Session() as sess:
            sess.run(init)
            train_batch = 0
            while train_batch < 100000:
                sess.run(opt)
                if train_batch%1000 == 0:
                    print("train_batch : %s" % train_batch)
                    print(loss.eval())
                train_batch += 1
            
            predict = y_test.eval()
        return predict

model = BaseModelV2()
y_test = model.train_predict(X, y_label, X_test)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, y_test, 'r-', label='Predict Line')
plt.grid()
plt.legend()

请添加图片描述

将模型改为变分推断模型：

from tensorflow.keras.activations import relu
from tensorflow.keras.optimizers import Adam
class VI():
    def __init__(self):
        self.prior_sigma_1 = 0.1
        self.prior_sigma_2 = 1.5
        self.w_0_mu = tf.Variable(tf.random.truncated_normal([1, 8], mean=0., stddev=1.))
        #self.w_0_sigma = tf.Variable(tf.random.truncated_normal([1, 8], mean=0., stddev=1.))
        self.w_0_sigma = tf.Variable(tf.zeros([1, 8]))
        
        self.b_0_mu = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.b_0_sigma = tf.Variable(tf.zeros([8]))
        
        self.w_1_mu = tf.Variable(tf.random.truncated_normal([8, 8], mean=0., stddev=1.))
        self.w_1_sigma =tf.Variable(tf.zeros([8, 8]))
        
        self.b_1_mu = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.b_1_sigma = tf.Variable(tf.zeros([8]))
        
        self.w_2_mu = tf.Variable(tf.random.truncated_normal([8, 1], mean=0., stddev=1.))
        self.w_2_sigma = tf.Variable(tf.zeros([8, 1]))
        
        self.b_2_mu = tf.Variable(tf.random.truncated_normal([1], mean=0., stddev=1.))
        self.b_2_sigma = tf.Variable(tf.zeros([1]))
        
        self.mu = [self.w_0_mu, self.b_0_mu, self.w_1_mu, self.b_1_mu, self.w_2_mu, self.b_2_mu]
        self.sigma = [self.w_0_sigma, self.b_0_sigma, self.w_1_sigma, self.b_1_sigma, self.w_2_sigma, self.b_2_sigma]     
    
    def sample_theta(self):
        self.w_0 = self.w_0_mu + tf.math.softplus(self.w_0_sigma) * tf.random.normal(self.w_0_mu.shape)
        self.b_0 = self.b_0_mu + tf.math.softplus(self.b_0_sigma) * tf.random.normal(self.b_0_mu.shape)
        self.w_1 = self.w_1_mu + tf.math.softplus(self.w_1_sigma) * tf.random.normal(self.w_1_mu.shape)
        self.b_1 = self.b_1_mu + tf.math.softplus(self.b_1_sigma) * tf.random.normal(self.b_1_mu.shape)
        self.w_2 = self.w_2_mu + tf.math.softplus(self.w_2_sigma) * tf.random.normal(self.w_2_mu.shape)
        self.b_2 = self.b_2_mu + tf.math.softplus(self.b_2_sigma) * tf.random.normal(self.b_2_mu.shape)
        self.theta = [self.w_0, self.b_0, self.w_1, self.b_1, self.w_2, self.b_2]
        
    
    def forward(self, x):
        x = tf.cast(x, tf.float32)
        
        self.sample_theta()
        h = relu(tf.matmul(x, self.w_0) + self.b_0)
        h = relu(tf.matmul(h, self.w_1) + self.b_1)
        y = tf.matmul(h, self.w_2) + self.b_2
        return y
    
    def gaussian_pdf(self, x, mu, sigma):
        return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
    
    def prior(self, x):
        # 混合高斯先验分布假设
        return 0.5 * self.gaussian_pdf(x, 0.0, self.prior_sigma_1) + 0.5 * self.gaussian_pdf(x, 0.0, self.prior_sigma_2)  
    
    def train_predict(self, x, label, x_test):
        y = self.forward(x)
        y_test = self.forward(x_test)
        
        loss = []
        for (theta, mu, sigma) in zip(self.theta, self.mu, self.sigma):
            q_theta_w = tf.math.log(self.gaussian_pdf(theta, mu, tf.math.softplus(sigma)) + 1e-30)
            p_theta = tf.math.log(self.prior(theta) + 1E-30)
            loss.append(tf.math.reduce_sum(q_theta_w - p_theta))       
        p_d_theta = tf.math.reduce_sum(tf.math.log(self.gaussian_pdf(label, y, 1.0) + 1E-30))
        loss.append(tf.math.reduce_sum(-p_d_theta))
        loss = tf.reduce_sum(loss)
        
        
        optimizer = tf.train.GradientDescentOptimizer(0.001, name="opt")
        gradient = optimizer.compute_gradients(loss)
        opt = optimizer.apply_gradients(gradient)
        init = tf.global_variables_initializer()
        with tf.Session() as sess:
            sess.run(init)
            train_batch = 0
            while train_batch < 100000:
                sess.run(opt)
                if train_batch%1000 == 0:
                    print("train_batch : %s" % train_batch)
                    print(loss.eval())
                train_batch += 1
            
            predict_num = 0
            predicts = []
            while predict_num < 300:
                predict = y_test.eval()
                predicts.append(predict)
                predict_num += 1
        return predicts
        

model = VI()
y_test = model.train_predict(X, y_label, X_test)
y_test = np.concatenate(y_test, axis=1)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_test, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_test, 2.5, axis=1), np.percentile(y_test, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()

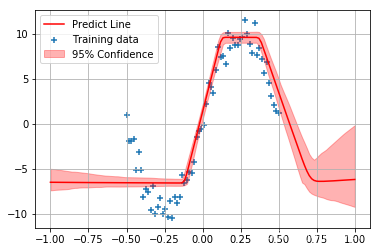
请添加图片描述

最后将模型改为条件变分自编码器：

from tensorflow.keras.activations import relu

class CVAE():
    def __init__(self):
        # prior
        self.z_dim = 8
        self.prior_w_mu = tf.Variable(tf.random.truncated_normal([1+1, self.z_dim], mean=0., stddev=1.))
        self.prior_b_mu = tf.Variable(tf.random.truncated_normal([self.z_dim], mean=0., stddev=1.))
        self.prior_w_mu_1 = tf.Variable(tf.random.truncated_normal([self.z_dim + 1, self.z_dim], mean=0., stddev=1.))
        self.prior_b_mu_1 = tf.Variable(tf.random.truncated_normal([self.z_dim], mean=0., stddev=1.))
      
        
        # encode
        self.encode_w_mu = tf.Variable(tf.random.truncated_normal([2+1, self.z_dim], mean=0., stddev=1.))
        self.encode_b_mu = tf.Variable(tf.random.truncated_normal([self.z_dim], mean=0., stddev=1.))
        self.encode_w_mu_1 = tf.Variable(tf.random.truncated_normal([self.z_dim+1, self.z_dim], mean=0., stddev=1.))
        self.encode_b_mu_1 = tf.Variable(tf.random.truncated_normal([self.z_dim], mean=0., stddev=1.))
        
        # decode
        self.w_1 = tf.Variable(tf.random.truncated_normal([self.z_dim + 1, 8], mean=0., stddev=1.))
        self.b_1 = tf.Variable(tf.random.truncated_normal([8], mean=0., stddev=1.))
        self.w_2 = tf.Variable(tf.random.truncated_normal([8 + 1, 1], mean=0., stddev=1.))
        self.b_2 = tf.Variable(tf.random.truncated_normal([1], mean=0., stddev=1.))
    
    def prior(self, x):
        # mu, sigma = PriorNet(x)
        ones = tf.ones_like(x)
        x = tf.concat([x, ones], axis=1)
        h = tf.math.sigmoid(tf.matmul(x, self.prior_w_mu) + self.prior_b_mu)
        h = tf.concat([h, ones], axis=1)
        p_mu = tf.matmul(h, self.prior_w_mu_1) + self.prior_b_mu_1
        with tf.variable_scope("cvae_prior_net", reuse=tf.AUTO_REUSE):
            p_sigma = tf.get_variable("prior_sigma",
                                      dtype=tf.float32,
                                      initializer=tf.zeros([self.z_dim]),
                                      trainable=True)
        return p_mu, p_sigma
    
    
    def encode(self, x, label):
        # mu, sigma = EncodeNet(x)
        ones = tf.ones_like(x)
        x = tf.concat([x, label, ones], axis=1)
        h = tf.math.sigmoid(tf.matmul(x, self.encode_w_mu) + self.encode_b_mu)
        h = tf.concat([h, ones], axis=1)
        q_mu = tf.matmul(h, self.encode_w_mu_1) + self.encode_b_mu_1
        with tf.variable_scope("cvae_encode_net", reuse=tf.AUTO_REUSE):
            q_sigma = tf.get_variable("encode_sigma",
                                      dtype=tf.float32,
                                      initializer=tf.zeros([self.z_dim]),
                                      trainable=True)
        return q_mu, q_sigma
    
    
    def sample(self, mu, sigma):
        return mu + tf.math.softplus(sigma) * tf.random.normal(tf.shape(mu))
    
    
    def decode(self, z):
        ones = tf.ones([tf.shape(z)[0], 1])
        z = tf.concat([z, ones], axis=1)
        h = tf.math.sigmoid(tf.matmul(z, self.w_1) + self.b_1)
        h = tf.concat([h, ones], axis=1)
        y = tf.matmul(h, self.w_2) + self.b_2
        return y
    
    
    def forward(self, x, label):
        p_mu, p_sigma = self.prior(x)
        q_mu, q_sigma = self.encode(x, label)
        z = self.sample(q_mu, q_sigma)
        y = self.decode(z)
        return p_mu, p_sigma, q_mu, q_sigma, z, y
    
    def predict(self, x):
        p_mu, p_sigma = self.prior(x)
        z = self.sample(p_mu, p_sigma)
        y = self.decode(z)
        return p_mu, p_sigma, z, y
    
    def gaussian_pdf(self, x, mu, sigma):
        return tf.compat.v1.distributions.Normal(mu, sigma).prob(x)
    
    def train_predict(self, x, label, x_test):
        x = tf.cast(x, tf.float32)
        label = tf.cast(label, tf.float32)
        p_mu, p_sigma, q_mu, q_sigma, z, y = self.forward(x, label)
        
        p_mu_test, p_sigma_test, z_test, y_test = self.predict(x_test)
        
        p_y_z = tf.reduce_sum(tf.math.log(self.gaussian_pdf(label, y, 1.0) + 1e-30))
        q_z_x = tf.reduce_sum(tf.math.log(self.gaussian_pdf(z, q_mu, tf.math.softplus(q_sigma)) + 1e-30))
        p_z_x = tf.reduce_sum(tf.math.log(self.gaussian_pdf(z, p_mu, tf.math.softplus(p_sigma)) + 1e-30))
        
        dkl = q_z_x - p_z_x
        loss = dkl - p_y_z
        
        optimizer = tf.train.GradientDescentOptimizer(0.001, name="opt")
        gradient = optimizer.compute_gradients(loss)
        opt = optimizer.apply_gradients(gradient)
        
        init = tf.global_variables_initializer()
        predict = []
        loss_list = []
        first_term = []
        sec_term = []
        with tf.Session() as sess:
            sess.run(init)
            print(p_y_z.eval())
            print(q_z_x.eval())
            print(p_z_x.eval())
            print(loss.eval())
            
            train_batch = 0
            while train_batch < 100000:
                sess.run(opt)
                if train_batch%100== 0:
                    loss_val = loss.eval()
                    loss_list.append(loss_val)
                    
                    dkl_val = dkl.eval()
                    first_term.append(dkl_val)
                    
                    p_y_z_eval = p_y_z.eval()
                    sec_term.append(p_y_z_eval)
                    print("train_batch : %s" % train_batch)
                    print(loss_val)
                    
                train_batch += 1
            
            predict_num = 0
            while predict_num < 300:
                predict.append(y_test.eval())
                predict_num += 1
        
        return predict, first_term, sec_term, loss_list
            
            
tf.reset_default_graph()            
model = CVAE()
y_preds, dkl, prob, losses = model.train_predict(X, y_label, X_test)
y_preds = np.concatenate(y_preds, axis=1)
plt.figure(figsize=(10,6))
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()

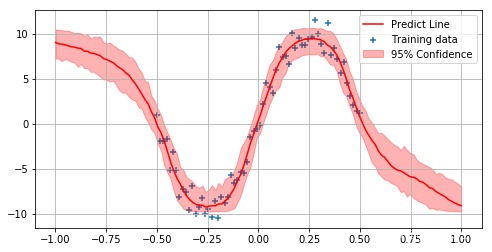
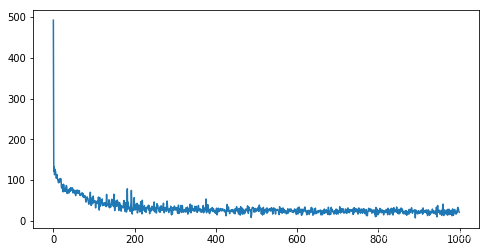
请添加图片描述
loss 的变化情况：
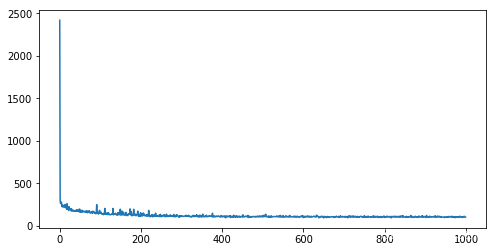
请添加图片描述
先验和后验分布的KL散度的变化情况：
请添加图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1508652.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【漏洞分析】CVE-2024-27198可RCE身份验证绕过JetBrains TeamCity

【漏洞分析】CVE-2024-27198可RCE身份验证绕过JetBrains TeamCity

CVE-2024-27198可RCE身份验证绕过JetBrains TeamCity 一、基本原理二、创建新的管理员用户三、自我检查四、POC 一、基本原理 向存在漏洞服务器发送一个不存在的页面请求 ?jsp/app/rest/server;.jsp 这会使服务器报错提供版本信息&#xff0c;且无需登录 Fofa app“JET_BRAIN…
阅读更多...
Linux工具 - 好用的yum包管理器

Linux工具 - 好用的yum包管理器

~~~~ 前言yum是什么为什么有yum如何使用yum配置用户yum源为什么要配置yum源具体配置备份CentOS-Base.repo文件下载对应阿里yum源到本目录/etc/yum.repos.d/清理yum并生成缓存更改配置文件CentOS-Base.repo更新yum 常用命令listinstall选项-y remove选项-y update 结语 前言 本…
阅读更多...
ON1 Portrait AI 2023：智能美颜，打造完美人像 mac版

ON1 Portrait AI 2023：智能美颜，打造完美人像 mac版

在数字化时代&#xff0c;人像摄影的需求和追求愈发高涨。为了满足摄影师对于完美人像的追求&#xff0c;ON1推出了全新的ON1 Portrait AI 2023。这款软件结合了先进的人工智能技术与人像处理的专业知识&#xff0c;为人像摄影带来了前所未有的智能体验。 ON1 Portrait AI 202…
阅读更多...
2024.3.11

2024.3.11

1.结构体数组 代码&#xff1a; #include<myhead.h>struct Stu {char name[100];int age;double score; };int main(int argc, const char *argv[]) {int i,j;struct Stu t{"z",1,1};struct Stu arr[4]{{"甲乙",12,98},{"陈二",13,77},{…
阅读更多...
docker启动时环境变量不生效（docker打包成镜像后环境变量失效）

docker启动时环境变量不生效（docker打包成镜像后环境变量失效）

前言 因项目需要多处部署&#xff0c;为了部署的方便&#xff0c;于是准备将项目环境打包成docker镜像以便于部署。mq、mysql这些在仓库中都有现成的镜像&#xff0c;虽然java和nginx的也都有&#xff0c;但是不知道当时是怎么想的&#xff0c;就不想搞太多镜像&#xff0c;也…
阅读更多...
五、OpenAI实战之Assistants API

五、OpenAI实战之Assistants API

在8线小城的革委会办公室里&#xff0c;黑8和革委会主任的对话再次展开。 黑8&#xff1a;主任&#xff0c;您知道吗&#xff1f;除了OpenAI API&#xff0c;现在还有一项新的技术叫做Assistants API&#xff0c;它可以帮助我们更好地进行对话和沟通。 主任&#xff1a;Assis…
阅读更多...
Redhat Linux(RHEL) - Primavera P6 EPPM 安装及分享

Redhat Linux(RHEL) - Primavera P6 EPPM 安装及分享

引言 继上一期发布的Oracle Linux版环境发布之后&#xff0c;近日我又制作了基于Redhat Linux 的P6虚拟机环境&#xff0c;同样里面包含了全套P6 最新版应用服务 此虚拟机仅用于演示、培训和测试目的。如您在生产环境中使用此虚拟机&#xff0c;请先与Oracle Primavera销售代表…
阅读更多...
SD-WAN能解决企业网络的哪些问题？

SD-WAN能解决企业网络的哪些问题？

SD-WAN技术的崛起为企业网络带来了全新的解决方案。在数字化转型、云计算、远程办公和5G等领域&#xff0c;SD-WAN技术展现出强劲的市场趋势。那么&#xff0c;SD-WAN究竟能够解决企业网络中的哪些难题呢&#xff1f; 提升网络带宽利用率 传统网络在连接分支机构时&#xff0c;…
阅读更多...
解决input事件监听拼音输入法导致高频事件

解决input事件监听拼音输入法导致高频事件

1、业务场景 在文本框中输入内容&#xff0c;执行查询接口&#xff0c;但遇到一个问题&#xff0c;当用拼音打字写汉字去搜索的时候&#xff0c;会输入一些字母拼成汉字&#xff0c;怎么能监听等拼音文字输入完成后再触发文本框监听事件 2、解决方案 通过查阅资料得知在输入中…
阅读更多...
Qt教程 — 1.3 如何创建Qt项目

Qt教程 — 1.3 如何创建Qt项目

目录 1 新建一个项目 2 项目文件介绍 2.1 项目文件夹介绍 2.2 配置文件*.pro 2.3 头文件*.h 2.4 源文件*.cpp 2.5 样式文件*.ui 3 修改 ui 文件 4 项目编译&调试&运行 4.1 运行 4.2 编译报错 1 新建一个项目 (1) 新建项目&#xff0c;方法一&#xff1a;打…
阅读更多...
Docker Desktop将镜像存储位置从C盘迁移到其它盘

Docker Desktop将镜像存储位置从C盘迁移到其它盘

一、简述 Docker Desktop默认安装在C盘，默认镜像存储位置在 C:\用户\Administrator\AppData\Local\Docker\wsl Docker Desktop 通过WSL2启动，会自动创建2个子系统，分别对应2个 vhdx 硬盘映像文件。 可以命令行执行wsl --list -v 看到 二、迁移步骤 1、在Docker Desktop…
阅读更多...
基于jsp+mysql+Spring+mybatis的SSM汽车保险理赔管理系统设计和实现

基于jsp+mysql+Spring+mybatis的SSM汽车保险理赔管理系统设计和实现

基于jspmysqlSpringmybatis的SSM汽车保险理赔管理系统设计和实现 博主介绍&#xff1a;多年java开发经验&#xff0c;专注Java开发、定制、远程、文档编写指导等,csdn特邀作者、专注于Java技术领域 作者主页 央顺技术团队 Java毕设项目精品实战案例《1000套》 欢迎点赞 收藏 ⭐…
阅读更多...
C++ 之LeetCode刷题记录（三十九）

C++ 之LeetCode刷题记录（三十九）

&#x1f604;&#x1f60a;&#x1f606;&#x1f603;&#x1f604;&#x1f60a;&#x1f606;&#x1f603; 开始cpp刷题之旅。 目标&#xff1a;执行用时击败90%以上使用 C 的用户。 22. 括号生成 数字 n 代表生成括号的对数&#xff0c;请你设计一个函数&#xff0c;用…
阅读更多...
在文件夹下快速创建vue项目搭建vue框架详细步骤

在文件夹下快速创建vue项目搭建vue框架详细步骤

一、首先在你的电脑目录下新建一个文件夹 进入该文件夹并打开控制台&#xff08;输入cmd指令&#xff09; 进入控制台后输入 vue create springboot_vue (自己指定名称) 如果出现这类报错如&#xff1a;npm install 的报错npm ERR! network request to http://registry.cnp…
阅读更多...
【JAVA重要知识 | 第八篇】Java注解总结

【JAVA重要知识 | 第八篇】Java注解总结

文章目录 8.注解8.1注解的定义8.1.1何为注解&#xff1f;8.1.2何为元数据和元编程&#xff1f;&#xff08;1&#xff09;元数据&#xff08;2&#xff09;元编程&#xff08;3&#xff09;总结 8.2注解的分类8.2.1常用的注解8.2.2自定义注解8.2.3元注解&#xff08;1&#xff…
阅读更多...
轻松掌握锁冲突问题的排查方法——《OceanBase诊断系列》之八

轻松掌握锁冲突问题的排查方法——《OceanBase诊断系列》之八

1. 前言 OceanBase数据库通过两阶段封锁机制确保读写事务并发控制的正确性。在高冲突场景下&#xff0c;事务处理中经常会遇到行锁冲突的问题。然而&#xff0c;许多OceanBase用户对于何时发生锁冲突&#xff0c;锁冲突的表现如何&#xff0c;以及如何排查锁冲突的原因&#x…
阅读更多...
python爬虫（6）之处理数组

python爬虫（6）之处理数组

1、拆分数组 1、spilt&#xff08;&#xff09;函数 此函数的用处是将数组均分成几个数组 演示如下&#xff1a; import numpy as np ac np.array([1,2,8,9,3,5,5,8]) ac1 np.split(ac,2) ac2 np.split(ac,[3,6]) print(ac1,ac2) 结果如下&#xff1a; 其中若是一个数…
阅读更多...
【计算机视觉】目标跟踪任务概述和算法介绍

【计算机视觉】目标跟踪任务概述和算法介绍

一、前言 1.1&#xff1a;目标跟踪VS目标检测&#xff1a;区别和联系 区别&#xff1a; 任务目标 目标跟踪任务的目标是在视频序列中跟踪一个特定目标的位置&#xff0c;即给定第一帧中的目标位置后&#xff0c;在后续帧中确定目标的位置。而目标检测任务的目标是在静态图像中…
阅读更多...
解决 Node.js 中 npm ERR! errno CERT_HAS_EXPIRED问题

解决 Node.js 中 npm ERR! errno CERT_HAS_EXPIRED问题

出自 BV1MN411y7pw&#xff0c; P94 黑马AJAX-Node.js-Webpack教学视频中npm包下载dayjs出错情况 输入 npm i dayjs指令之后出错&#xff1a; npm ERR! errno CERT_HAS_EXPIREDnpm ERR! A complete log of this run can be found in: C:\Users\24541\AppData\Local\npm-cache…
阅读更多...
【leetcode C++】最小栈

【leetcode C++】最小栈

leetcode 155. 最小栈 题目 设计一个支持 push &#xff0c;pop &#xff0c;top 操作&#xff0c;并能在常数时间内检索到最小元素的栈。 实现 MinStack 类: MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023