目录
选择题
编程题
数字在升序数组中出现的次数
整数转换
选择题
1、如下程序的功能是
#include <stdio.h>
int main()
{
char ch[80] = "123abcdEFG*&";
int j;
puts(ch);
for(j = 0; ch[j] != '\0'; j++)
{
if(ch[j] >= 'A' && ch[j] <= 'Z')
ch[j] = ch[j] + 'e' - 'E';
}
puts(ch);
return 0;
}- A 测字符数组
ch的长度 - B 将数字字符串
ch转换成十进制数 - C 将字符数组
ch中的小写字母转换成大写 - D 将字符数组
ch中的大写字母转换成小写
答案:D
解析:
在ASCII中,大写字母和小写字母相差32,故有'e'-'E'为32,而在条件判断语句的条件中,只有当数组元素为大写字母才会进入分支,故字符数组中的每一个大写字母都会加上32,即转化为其对应的小写字母
2、对于代码段,下面描述正确的是
t=0;
while(printf("*"))
{
t++;
if (t<3)
break;
}- A 其中循环控制表达式与0等价
- B 其中循环控制表达式与'0'等价
- C 其中循环控制表达式是不合法的
- D 以上说法都不对
答案:B
解析:
因printf(“*”)函数调用的返回值是字符串中字符的个数,即为1。所以while后面的条件恒为真,所以循环控制表达式与'0'是等价的(字符'0'不是0)
3、以下程序运行时,若输入 1abcedf2df<回车> 输出结果是
#include <stdio.h>
int main()
{
char ch;
while((ch = getchar()) != '\n')
{
if(ch % 2 != 0 && (ch >= 'a' && ch <= 'z'))
ch = ch 'a' + 'A';
putchar(ch);
}
printf("\n");
return 0;
}- A 1abcedf2df
- B 1ABCEDF2DF
- C 1AbCEdf2df
- D 1aBceDF2DF
答案:C
解析:
程序首先考虑ch的ASCII 码值是不是奇数,再看是不是小写字母,同时满足时被改为大写字母
4、下列条件语句中,功能与其他语句不同的是
- A
if(a) printf("%d\n",x); else printf("%d\n",y); - B
if(a==0) printf("%d\n",y); else printf("%d\n",x); - C
if (a!=0) printf("%d\n",x); else printf("%d\n",y); - D
if(a==0) printf("%d\n",x); else printf("%d\n",y);
答案:D
解析:
除了D选项以外,其他都是a==0时输出y,a!=0时输出x
5、(多选题)我们知道C语言的 break 语句只能跳出离它最近的一层循环,可是有时候我们需要跳出多层循环,下列跳出多层循环的做法正确的是
- A 将程序写成函数用
return结束函数,便可跳出循环 - B 修改外层循环条件例如
for( int i = 0 ; i < MAX1 ; i ++ )
{
for( int j = 0 ; j < MAX2 ; j ++ )
{
if(condition)
{
i = MAX1;
break;
}
}
}- C 在外层循环设置判断条件例如
for( ; symbo != 1 && condition2; )
{
for( ; symbo != 1 && condition3; )
{
if(condition1)
symbol = 1;
}
}- D 在外层循环后面加入
break例如
for( ; condition2; )
{
for( ; condition3; )
{
if(condition1)
symbol = 1;
}
if(symbol == 1)
break;
}答案:ABCD
解析:
当循环被封装到函数中时,因为return语句可以结束函数的继续执行,故可以跳出循环;对于B选项来说,因为第一层循环满足i<MAX1时才会继续执行,而在if中,讲MAX1的数值给了i再break,首先会推出内层循环,其次因为i等于MAX1导致第一个循环也结束执行,所以跳出循环;对于C选项来说,if语句中将symbol的值改为了1,导致两层循环的判断条件都为假,从而跳出循环;对于D选项来说,break在外层循环,可以跳出该层循环,同时直接终止所有内层循环执行
编程题
数字在升序数组中出现的次数
题目链接:数字在升序数组中出现的次数_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个长度为 n 的非降序数组和一个非负数整数 k ,要求统计 k 在数组中出现的次数
数据范围:0≤ n≤1000,0≤ k≤100,数组中每个元素的值满足0≤ val≤100
要求:空间复杂度 O(1),时间复杂度 O( logn)
思路解析:
第一种思路,通过双指针法进行求解,一个指针left从数组的左侧向中间寻找,另一个指针right从数组的右侧向中间寻找,当两个指针各自遇到了等于数值k时,计数器各加1,但是这个方法存在一个问题,如果数组中只有一个数据时,并且这个数据等于k,那么left指针会加1次,right指针也会加1次导致多次计算,使用在循环判定时,不要使用等于,将二者相等作为退出循环条件,此时再出现上面的情况时,只需要单独计数器加1即可
第二种思路,使用二分查找算法进行求解,因为题目给定的数组是一个非降序的数组,但是二分查找算法不可以直接查找存在大量重复数值的数组,使用此题不能通过二分查找直接找等于k的数值。那么此题如何使用二分算法求解,可以考虑下面的思路:通过二分查找算法找到k值的边界值的下标,包括上界下标和下界下标,两个界限下标的差值即为等于k出现的次数,可以考虑使用k+0.5和k-0.5来作为边界值,具体思路如下:
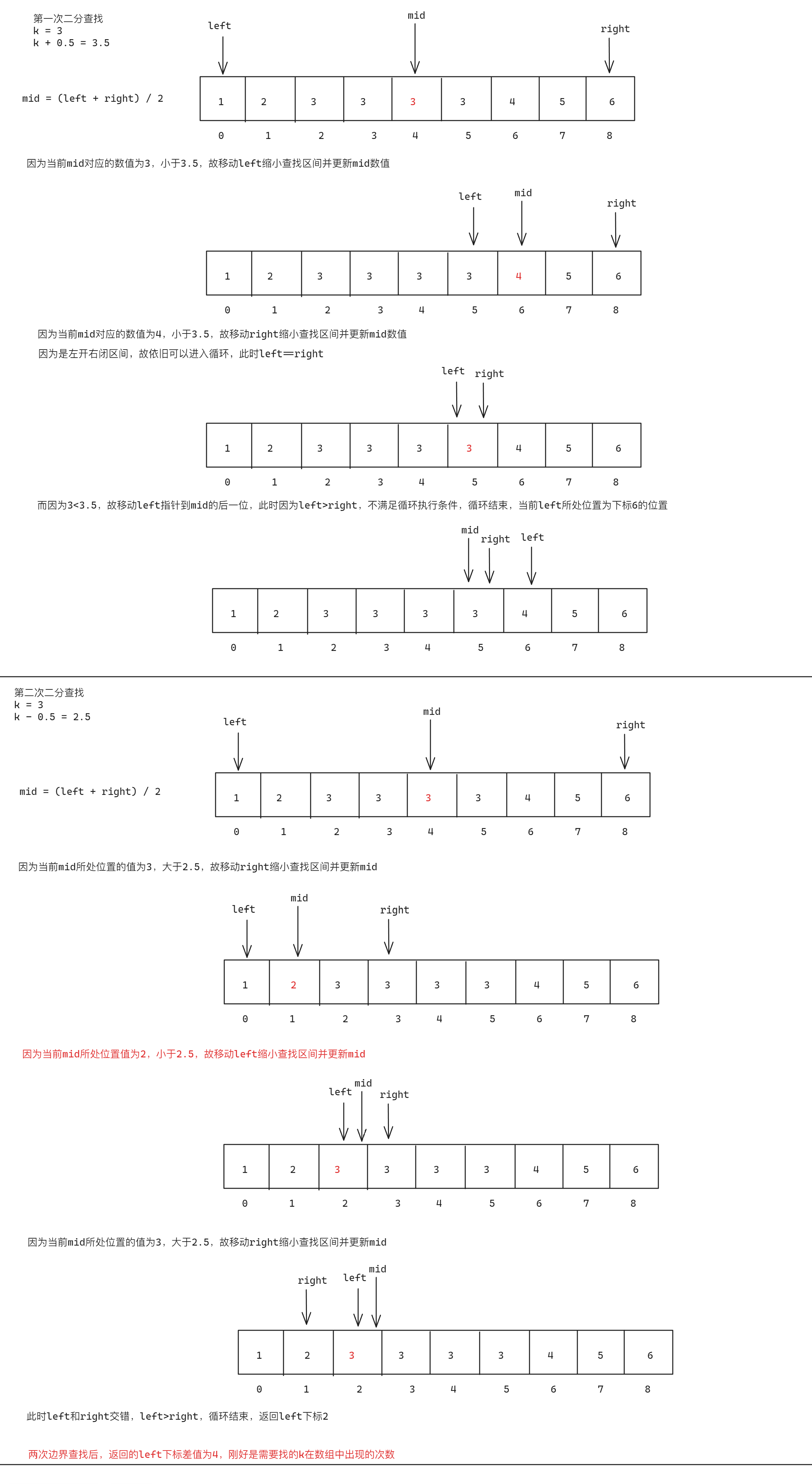
参考代码
第一种方法
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @param k int整型
* @return int整型
*/
int GetNumberOfK(int* nums, int numsLen, int k ) {
int left = 0;
int right = numsLen - 1;
int count = 0;
while (left < right) {
if(nums[left] == k)
{
count++;
}
if(nums[right] == k)
{
count++;
}
left++;
right--;
}
if(left == right && nums[left] == k)
{
count++;
}
return count;
}第二种方法
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param nums int整型一维数组
* @param numsLen int nums数组长度
* @param k int整型
* @return int整型
*/
//二分查找
int BinarySearch(int* nums, int numsLen, double k)
{
int left = 0;
int right = numsLen - 1;
while (left <= right) {
int mid = (left + right) / 2;
if(nums[mid] > k)
{
right = mid - 1;
}
else if (nums[mid] < k) {
left = mid + 1;
}
}
//返回 left 而不是 mid
return left;
}
int GetNumberOfK(int* nums, int numsLen, int k ) {
return BinarySearch(nums, numsLen, k+0.5)-BinarySearch(nums, numsLen, k-0.5);
}整数转换
题目链接:面试题 05.06. 整数转换 - 力扣(LeetCode
整数转换。编写一个函数,确定需要改变几个位才能将整数A转成整数B。
示例1:
输入:A = 29 (或者0b11101), B = 15(或者0b01111)
输出:2
示例2:
输入:A = 1,B = 2
输出:2
提示:
A,B范围在[-2147483648, 2147483647]之间
思路解析:
本题可以考虑使用异或操作找出两个数值之间不同的位置,根据异或的特点,两个数存在相异的位置时异或结果为1,接着因为整数的比特位个数在力扣上是32位,故可以考虑右移i位与1相与,如果结果为1,那么说明是不同的位置,否则是相同的位置,记录不同的位置即可
参考代码
/*
* @lc app=leetcode.cn lang=c
*
* 整数转换
*/
// @lc code=start
int convertInteger(int A, int B){
int ret = A^B;
int count = 0;
for(int i = 0; i < 32; i++)
{
if((ret >> i) & 1 == 1)
{
count++;
}
}
return count;
}
// @lc code=end