目录
队列的应用场景
1、429. N 叉树的层序遍历
2、 103. 二叉树的锯齿形层序遍历
3、662. 二叉树最大宽度
4、515. 在每个树行中找最大值
队列的应用场景
-
广度优先搜索(BFS):队列是广度优先搜索算法的核心数据结构。在BFS中,我们从根节点开始,逐层地访问节点,首先访问根节点,然后访问其所有直接子节点,然后是子节点的子节点,以此类推。队列用于按照层级顺序存储待访问的节点,确保先访问上一层的节点,然后再访问下一层的节点。
-
树的层次遍历:在树的层次遍历算法中,队列用于按层级顺序存储待访问的节点。这样可以确保先访问上一层的节点,然后再访问下一层的节点。
1、429. N 叉树的层序遍历
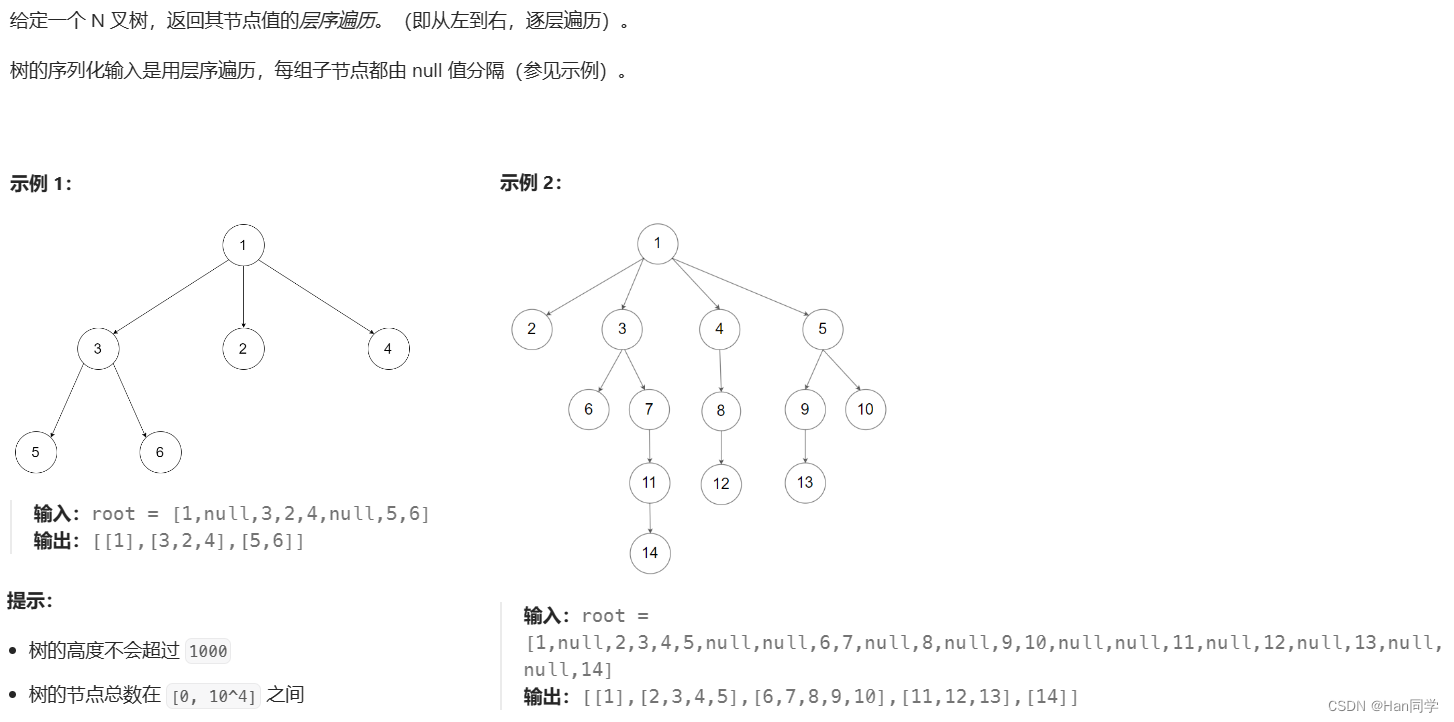
思路:队列实现广度优先搜索(dfs)。
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val) {
val = _val;
}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> ret;//存储返回结果
queue<Node*> q;
if (root == nullptr)//处理空树
return ret;
q.push(root);
while (q.size()) {//某层元素个数为0则结束
vector<int> tmp;//暂存当前层的元素
int n = q.size();
for (int i = 0; i < n; i++) {//循环处理当前层
Node* s = q.front();
q.pop();//弹出队列
tmp.push_back(s->val);//存入暂存数组
//每处理完一个元素,它的孩子节点需要入队列
for (Node* child : s->children) {/
if (child != nullptr)
q.push(child);
}
}
ret.push_back(tmp);//存入当前层的结果
}
return ret;
}
};2、 103. 二叉树的锯齿形层序遍历
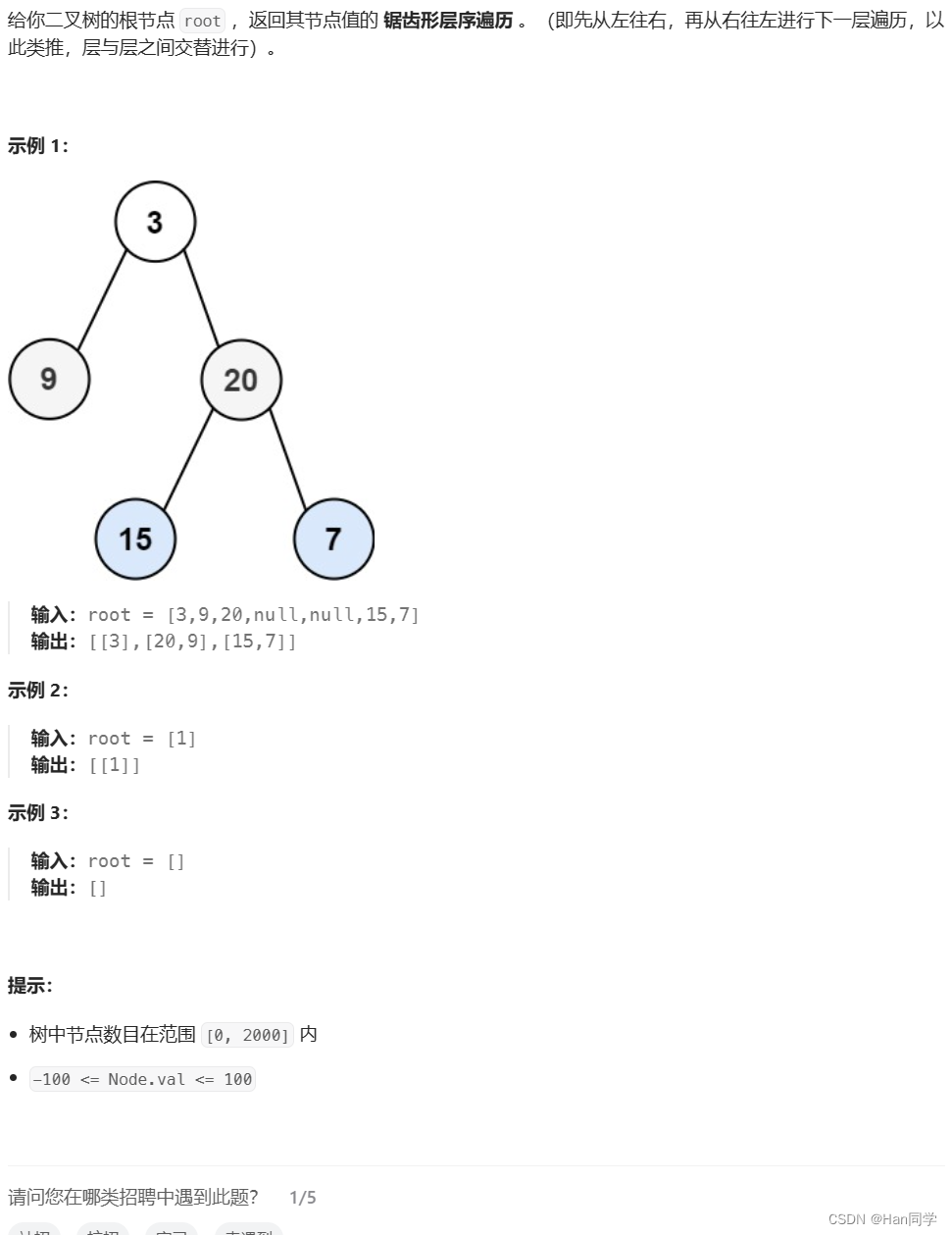
思路:队列实现广度优先搜索(dfs),偶数层进行逆置即可实现锯齿形层序遍历。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret;
if (root == nullptr)
return ret;
queue<TreeNode*> q;
int level = 1;
q.push(root);
while (q.size()) {
int sz = q.size();
vector<int> tmp;
for (int i = 0; i < sz; i++) {
TreeNode* t = q.front();
q.pop();
tmp.push_back(t->val);
if (t->left)
q.push(t->left);
if (t->right)
q.push(t->right);
}
if (level % 2 == 0)
reverse(tmp.begin(), tmp.end());
ret.push_back(tmp);
level++;
}
return ret;
}
};3、662. 二叉树最大宽度

思路:数组模拟二叉树建堆思路,使用数组或队列统计下标并计算差值即可。
题中说题目数据保证答案将会在 32 位 带符号整数范围内,所以使用unsigned int存储下标差值。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
vector<pair<TreeNode*, unsigned int>> q;
unsigned int ret = 0;
q.push_back({root, 1});
while (q.size()) {
auto& x = q.front();
auto& y = q.back();
ret = max(ret, y.second - x.second + 1);
vector<pair<TreeNode*, unsigned int>> tmp;//存储下一层
for (auto& x : q) {
if (x.first->left)
tmp.push_back({x.first->left, x.second * 2});
if (x.first->right)
tmp.push_back({x.first->right, 2 * x.second + 1});
}
q = tmp;//更新为下一层
}
return ret;
}
};4、515. 在每个树行中找最大值
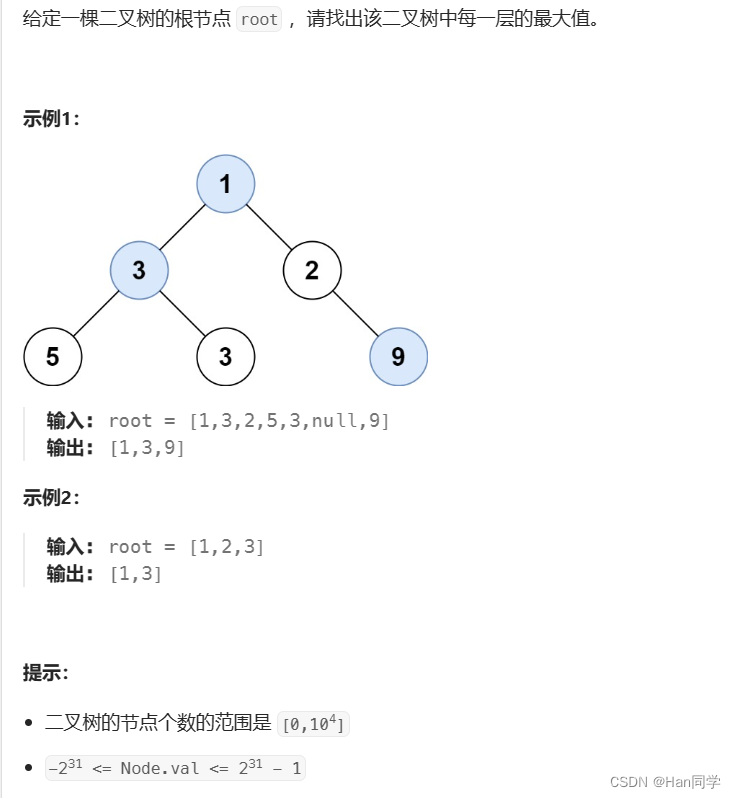
思路:队列实现广度优先搜索(dfs)。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> ret;
if (root == nullptr)
return ret;
queue<TreeNode*> q;
q.push(root);
while (q.size()) {
int sz = q.size();
int tmp = INT_MIN;
for (int i = 0; i < sz; i++) {//便利当前层
TreeNode* t = q.front();
q.pop();
tmp = max(tmp, t->val);//记录当前层最大值
//更新当前元素的子节点到队列
if (t->left)
q.push(t->left);
if (t->right)
q.push(t->right);
}
ret.push_back(tmp);
}
return ret;
}
};