C语言分析基础排序算法—

交换排序

冒泡排序

快速排序

Hoare版本快速排序

挖坑法快速排序

前后指针法快速排序

快速排序优化

快速排序非递归版

交换排序

冒泡排序

见C语言基础知识指针部分博客C语言指针-CSDN博客

快速排序

Hoare版本快速排序

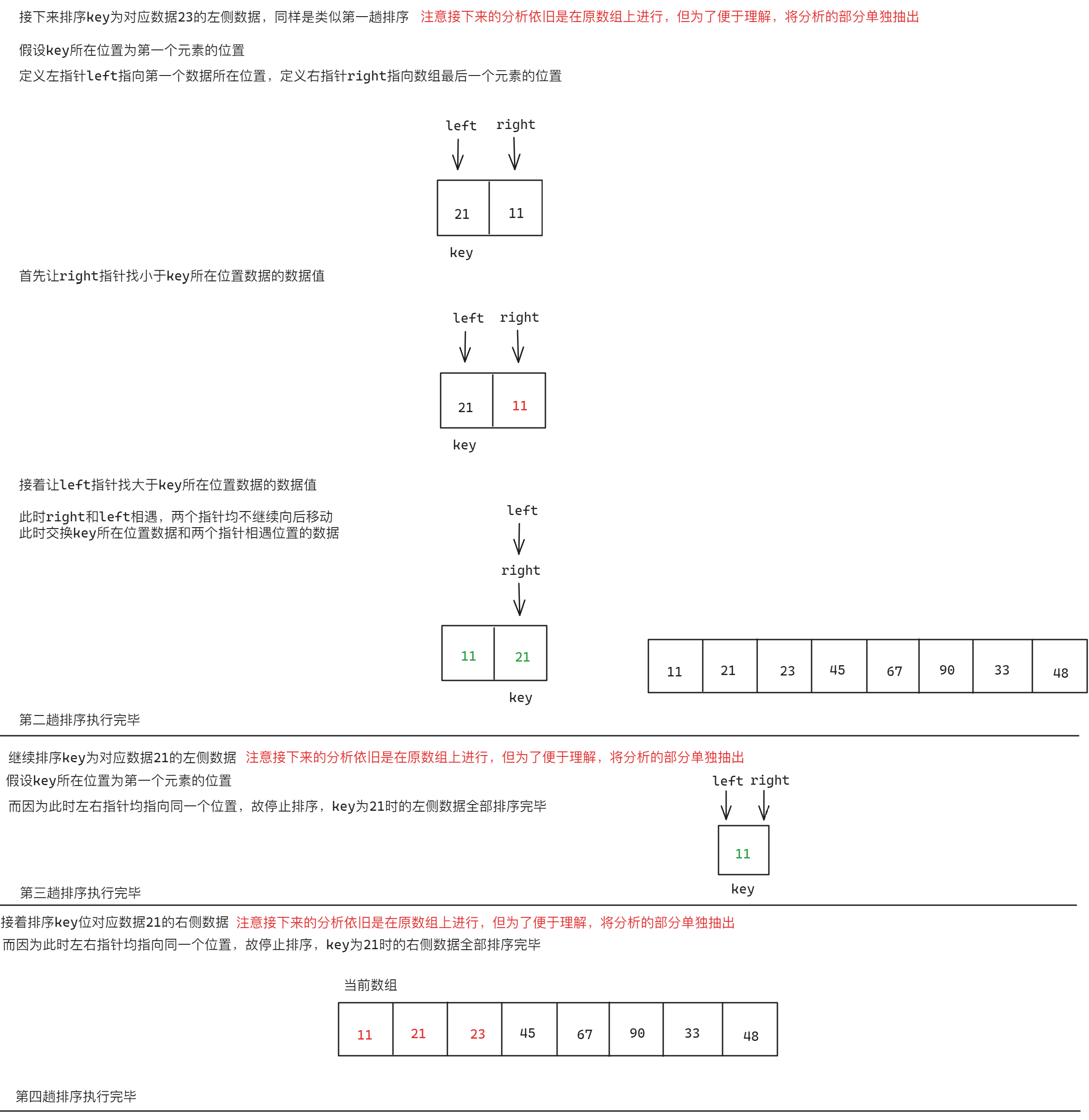
Hoare版本快速排序的过程类似于二叉树前序遍历的过程，基本思想是：在需要排序的数据中确定一个值放入key中，接着使用左指针和右指针从数据的起始位置以及数据的末端位置向中间遍历，左指针找数值比key大的数据，右指针找数值比key小的数据，交换这两个指针的数据之后接着向中间移动，直到两个指针最后相遇时交换key所在的数值以及相遇位置的数值，完成第一趟排序，接着进行左边部分的排序，方法如同第一趟排序，左边排序完毕后进行右边部分的排序，方法如同第二趟排序，直到最后全部排序完成后为止。具体思路如下：

📌

注意key是数值的下标

//以下面的数组为例
int data[] = { 23,48,67,45,21,90,33,11 };

下面是完整过程递归图

参考代码

void swap(int* num1, int* num2)
{
    int tmp = *num1;
    *num1 = *num2;
    *num2 = tmp;
}

//一趟排序，返回key指向的位置
int PartSort(int* data, int left, int right)
{
    int key = left;//使key指向区间的第一个元素位置
    while (left < right)
    {
        //先让右侧指针先走，右指针找小
        while (left < right && data[right] >= data[key])
        {
            right--;
        }
        //再让左侧指针走，左侧指针找大
        while (left < right && data[left] <= data[key])
        {
            left++;
        }
        
        //交换右侧指针和左侧指针的数据
        swap(&data[right], &data[left]);
    }
    //执行完循环后，交换key所在位置的数据和right与left指针相遇的位置的数值
    swap(&data[key], &data[left]);
    //返回交换后的key指向的元素的位置
    return left;
}

//Hoare版本
void QuickSort_Hoare(int* data, int left, int right)
{
    //当left和right指针指向同一个位置或后一个位置结束排序
    if (left >= right)
    {
        return;
    }

    //获取到当前key的位置
    int key = PartSort(data, left, right);

    QuickSort_Hoare(data, left, key - 1);
    QuickSort_Hoare(data, key + 1, right);
}

Hoare版本问题分析

在上面的过程分析中，使用第一个元素的位置作为key的位置，也可以使用最后一个元素作为key的位置，但是需要注意的是，以key指向第一个元素的位置为例，left指针一定需要指向第一个元素，而不是从第二个元素开始，例如下面的情况：当key位置的数据比其他数据都小时，right找小将一直向key所在位置移动

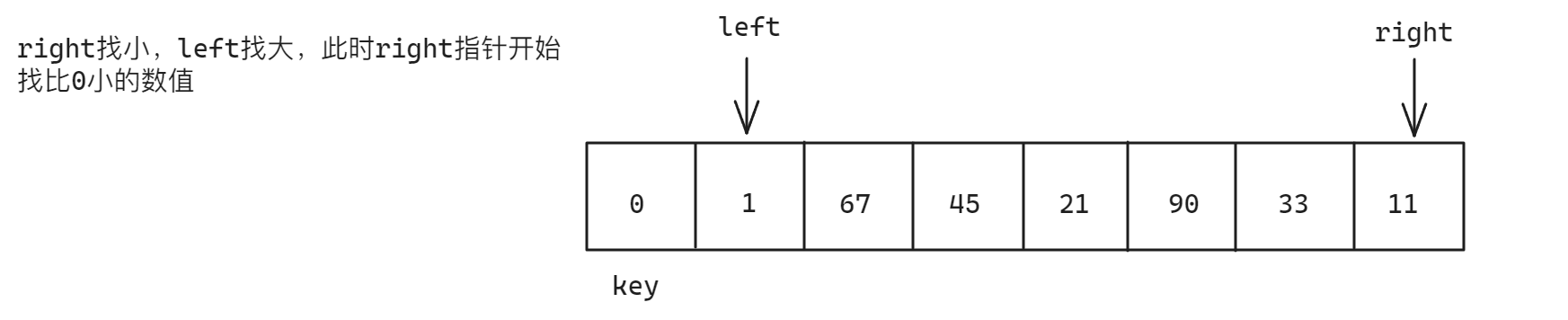
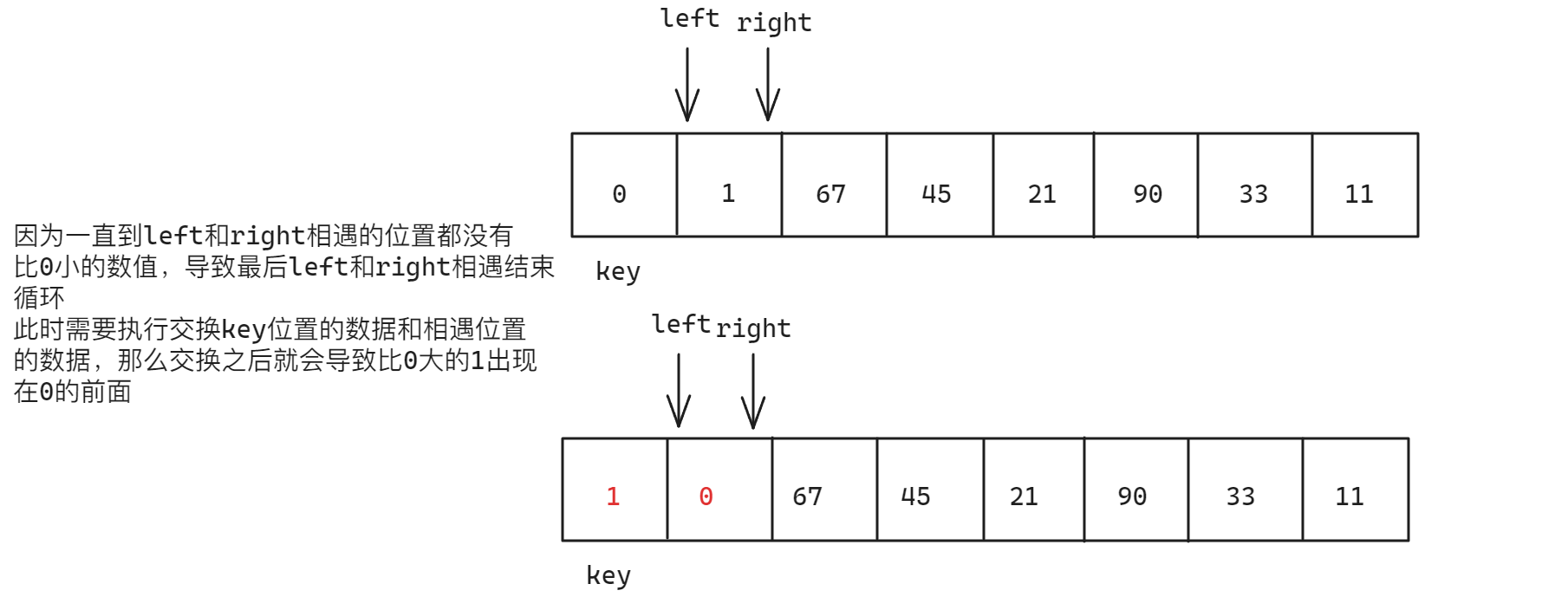
在判断left指针或者right指针是否需要移动时，需要包括等于的情况，否则会进入死循环，例如下面的情况：当left和right指针同时指向一个等于key所在位置的元素

对于递归结束的条件来说，需要出现left指针的值大于或者等于right指针的值，而不是仅仅一个大于或者等于，因为返回相遇的位置，即返回left指针或者right指针的位置而不是实际返回key所在位置，在交换过程中，只是交换key对应位置的数值和相遇位置的数值，并没有改变key指向的位置
对于left指针和right指针相遇的位置的数值一定比key所在位置的数值小的问题，下面是基本分析：

分析主问题之前，先分析right比left指针先走的原因：在初始位置时，left指针和right指针各指向第一个元素和最后一个元素但是left指针与key指针指向的位置相同，此时让right指针先走，而不是left指针先走，反之同理，具体原因如下：

接下来分析当right指针比left指针先走时，两个指针相遇时一定相遇到一个比key小的数值的问题

两个指针相遇的方式有两种情况

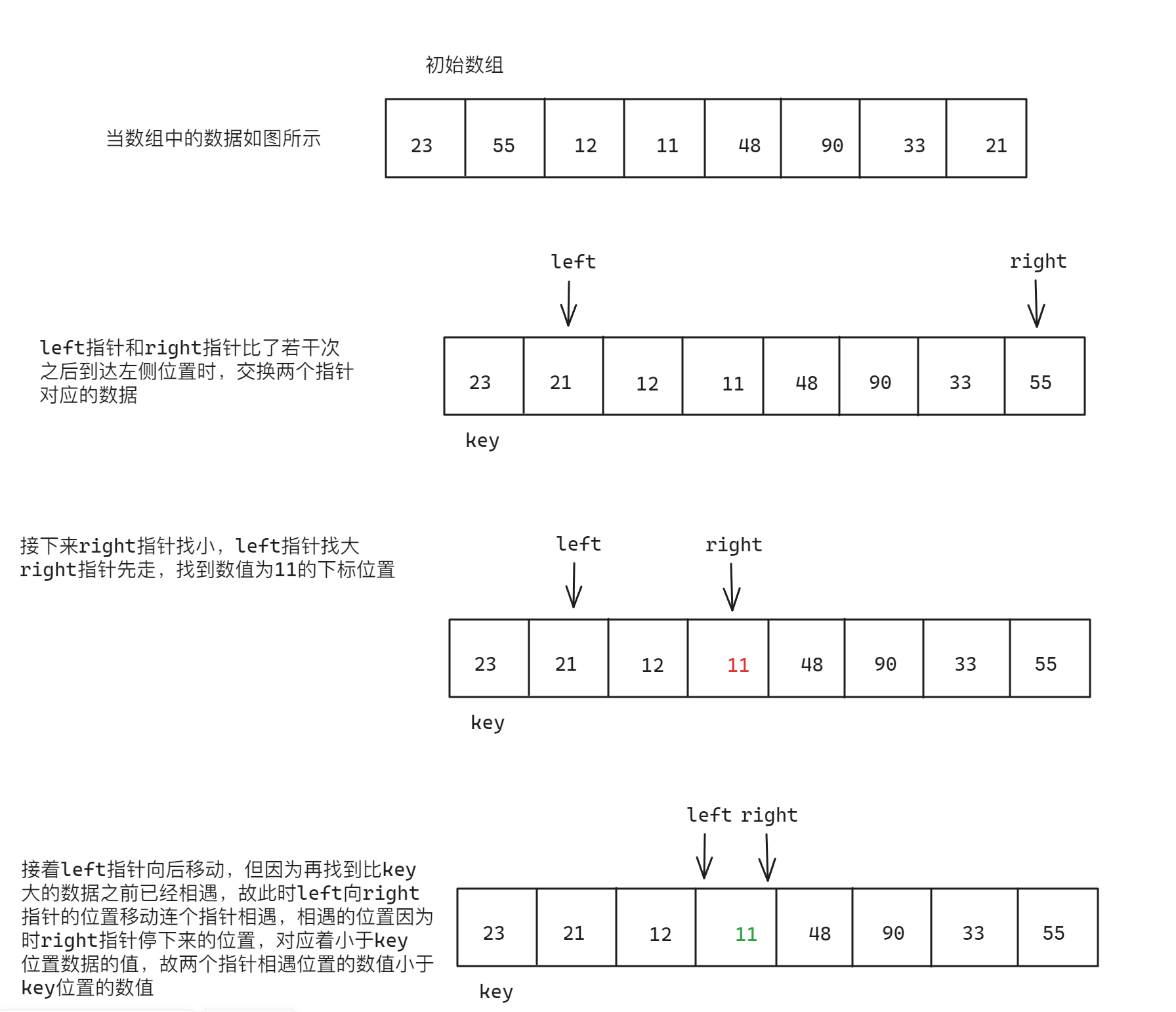
第一种情况：left指针向right指针移动与其相遇
第二种情况：right指针向left指针移动与其相遇

对于第一种情况，分析如下：

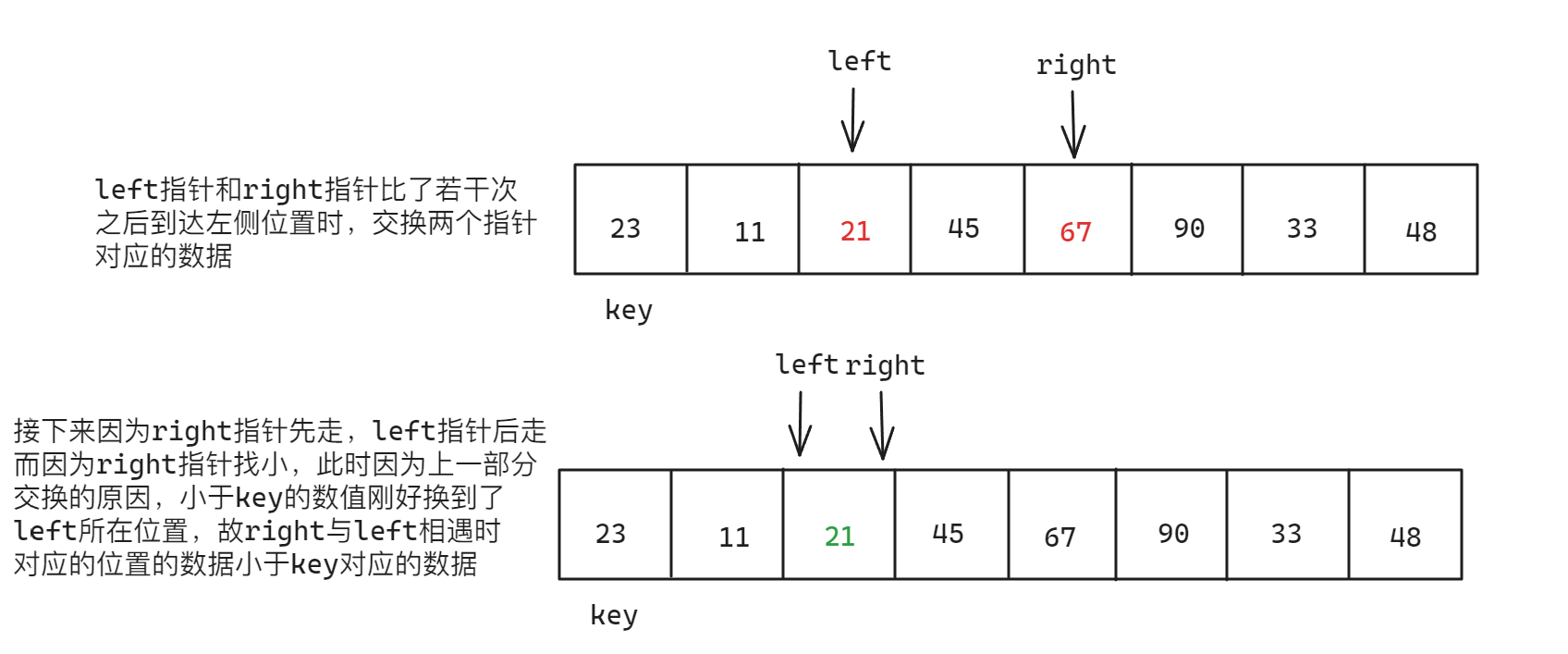
对于第二种情况，分析如下：

挖坑法快速排序

挖坑法快速排序相较于Hoare版本的快速排序没有效率上的优化，但是在理解方式上相对简单，其基本思路为：在数据中随机取出一个数值放入key变量中，此时该数值的位置即为一个坑位，接下来left指针从第一个元素开始key值大的数值，right指针从最后一个元素找比key值小的数值，此时不用考虑left指针和right指针谁先走，考虑right指针先走，当right指针找到小时，将该值放置到hole所在位置，更新hole到right指针的位置，接下来left指针找大，当left指针找到较key大的数值时，将该数值存入hole中，更新hole为left所在位置，如此往复，直到第一趟排序结束。接着进行左边部分的排序，方法如同第一趟排序，左边排序完毕后进行右边部分的排序，方法如同第二趟排序，直到最后全部排序完成后为止。具体思路如下：

📌

注意key是数值

//以下面的数组为例
int data[] = { 23,48,67,45,21,90,33,11 };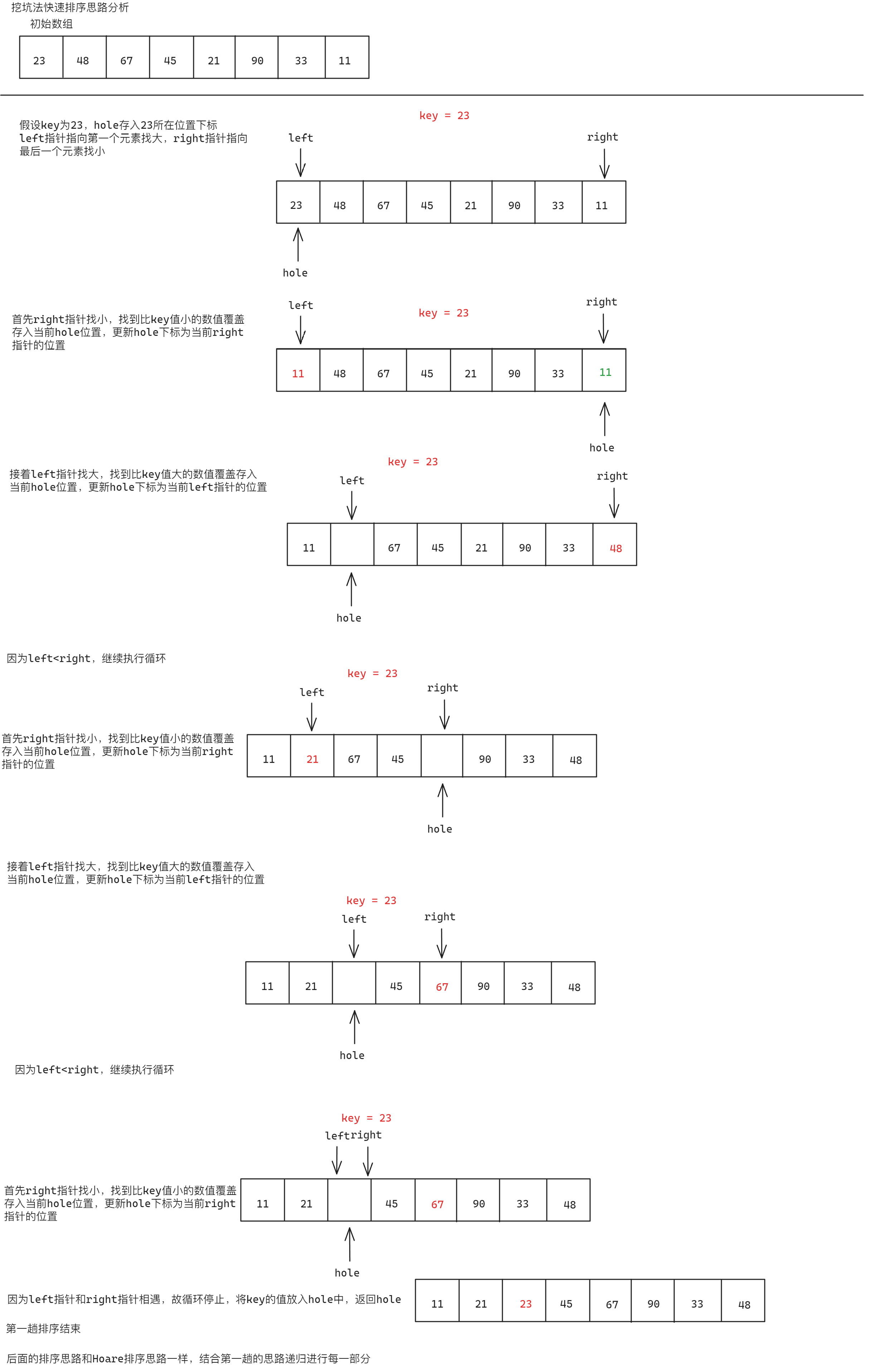

int PartSort_DigHole(int* data, int left, int right)
{
    int hole = left;
    int key = data[left];
    while (left < right)
    {
        while (left < right && data[right] >= key)
        {
            right--;
        }
        data[hole] = data[right];
        hole = right;
        while (left < right && data[left] <= key)
        {
            left++;
        }
        data[hole] = data[left];
        hole = left;
    }
    data[hole] = key;
    return hole;
}

//挖坑法
void QuickSort_DigHole(int* data, int left, int right)
{
    if (left >= right)
    {
        return;
    }

    int hole = PartSort_DigHole(data, left, right);

    QuickSort_DigHole(data, left, hole - 1);
    QuickSort_DigHole(data, hole + 1, right);
}

前后指针法快速排序

前后指针法相对Hoare版本和挖坑法也没有效率上的优化，但是理解相对容易，基本思路如下：在前后指针法中，有一个key指针，该指针指向一个随机的数值的下标位置，接下来是一个prev指针，指向数据的第一个元素的下标位置，以及一个cur指针指向第二个元素的下标位置，cur指针和prev指针向前遍历，当遇到比key小的数值时，prev指针先移动柜，再进行cur和prev进行对应位置的数值交换，接着cur指着移动，否则只让cur指针移动，当cur走到数据的结尾时结束循环，交换prev和key指针的数据，完成第一趟排序。接着进行左边部分的排序，方法如同第一趟排序，左边排序完毕后进行右边部分的排序，方法如同第二趟排序，直到最后全部排序完成后为止。具体思路如下：

📌

注意key是数值的下标，并且用left和right控制递归区间

int PartSort_Prev_postPointer(int *data, int left, int right)
{
    int key = left;
    int cur = left + 1;
    int prev = left;
    while (cur <= right)
    {
        //++prev != cur可以防止cur和自己本身交换导致多交换一次
        if (data[cur] < data[key] && ++prev != cur)
        {
            prev++;
            swap(&data[cur], &data[prev]);
        }
        cur++;
    }
    swap(&data[prev], &data[key]);
    return prev;
}

//前后指针法
void QuickSort_Prev_postPointer(int* data,int left, int right)
{
    if (left >= right)
    {
        return;
    }

    int key = PartSort_Prev_postPointer(data, left, right);

    QuickSort_Prev_postPointer(data, left, key - 1);
    QuickSort_Prev_postPointer(data, key + 1, right);
}

快速排序优化

在快速排序优化部分，采用三数取中的思路对快速排序有大量重复数据或者有序情况下进行优化，所谓三数取中，即第一个元素的位置和最后一个元素的位置加和取一半的数值在数据中的位置，但是此时需要注意的是key当前位置为mid所在位置，为了不改变原来的快速排序代码，获得中间值下标时，交换key位置的值和mid位置的值即可

//三数取中
int GetMidIndex(int* data, int left, int right)
{
    int mid = (left + right) / 2;
    //获取左、中、有三个数中的中间数
    if (data[left] > data[mid])
    {
        if (data[mid] > data[right])
        {
            //left>mid>right
            return mid;
        }
        else if (data[left] > data[right])
        {
            //left>right>mid
            return right;
        }
        else
        {
            //right>left>mid
            return left;
        }
    }
    else
    {
        if (data[mid] < data[right])
        {
            //right>mid>left
            return mid;
        }
        else if (data[right] > data[left])
        {
            //mid>right>left
            return right;
        }
        else
        {
            //mid>left>right
            return left;
        }
    }
}

以前后指针版本修改为例

#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <assert.h>

void swap(int* num1, int* num2)
{
    int tmp = *num1;
    *num1 = *num2;
    *num2 = tmp;
}

//三数取中
int GetMidIndex(int* data, int left, int right)
{
    int mid = (left + right) / 2;
    //获取左、中、有三个数中的中间数
    if (data[left] > data[mid])
    {
        if (data[mid] > data[right])
        {
            //left>mid>right
            return mid;
        }
        else if (data[left] > data[right])
        {
            //left>right>mid
            return right;
        }
        else
        {
            //right>left>mid
            return left;
        }
    }
    else
    {
        if (data[mid] < data[right])
        {
            //right>mid>left
            return mid;
        }
        else if (data[right] > data[left])
        {
            //mid>right>left
            return right;
        }
        else
        {
            //mid>left>right
            return left;
        }
    }
}

int PartSort_Prev_postPointer(int *data, int left, int right)
{
    int mid = GetMidIndex(data, left, right);
    swap(&data[left], &data[mid]);
    int key = left;
    int cur = left + 1;
    int prev = left;
    while (cur <= right)
    {
        //++prev != cur可以防止cur和自己本身交换导致多交换一次
        if (data[cur] < data[key] && ++prev != cur)
        {
            swap(&data[cur], &data[prev]);
        }
        cur++;
    }
    swap(&data[prev], &data[key]);
    return prev;
}

//前后指针法
void QuickSort_Prev_postPointer(int* data,int left, int right)
{
    if (left >= right)
    {
        return;
    }

    int key = PartSort_Prev_postPointer(data, left, right);

    QuickSort_Prev_postPointer(data, left, key - 1);
    QuickSort_Prev_postPointer(data, key + 1, right);
}

int main()
{
    int data[] = { 23,48,67,45,21,90,33,11 };
    int sz = sizeof(data) / sizeof(int);
    QuickSort_Prev_postPointer(data, 0, sz - 1);
    for (int i = 0; i < sz; i++)
    {
        printf("%d ", data[i]);
    }

    return 0;
}
输出结果：
11 21 23 33 45 48 67 90

快速排序非递归版

由于递归的函数栈帧空间是在栈上创建的，而且栈上的空间较堆空间小，所以当数据量太大时，可以考虑用快速排序的非递归版，一般用栈来实现，基本思路如下：首先将数据的头和尾进行入栈操作，再在循环中通过出栈和获取栈顶元素控制左区间和右区间，可以先执行左区间或者右区间，本处以先右区间再左区间为例，通过需要拆分数据的部分出栈排序，再接着重复步骤最后排序完成，具体思路分析如下：

void QuickSort_NotRecursion(int* data, int left, int right)
{
    ST st = { 0 };
    STInit(&st);
    //压入第一个元素和最后一个元素所在位置
    STPush(&st, left);
    STPush(&st, right);

    while (!STEmpty(&st))
    {
        //获取区间
        int right = STTop(&st);
        STPop(&st);
        int left = STTop(&st);
        STPop(&st);

        //单趟排序
        int key = PartSort_Hoare(data, left, right);

        //更新区间
        //先压右侧区间
        if (key + 1 < right)
        {
            STPush(&st, key + 1);
            STPush(&st, right);
        }

        //再压左侧区间
        if (left < key - 1)
        {
            STPush(&st, left);
            STPush(&st, key - 1);
        }
    }

    STDestroy(&st);
}

快速排序的时间复杂度为 $O(N\times log_{2}{N})$ ，空间复杂度为 $O(log_{2}{N})$ ，属于不稳定算法