好文分享:【数据结构】线段树(Segment Tree) - 小仙女本仙 - 博客园
线段树和树状数组的基本功能都是在某一满足结合律的操作(比如加法,乘法,最大值,最小值)下,O(logn)的时间复杂度内修改单个元素并且维护区间信息。
不同的是,树状数组只能维护前缀“操作和”(前缀和,前缀积,前缀最大最小),而线段树可以维护区间操作和。
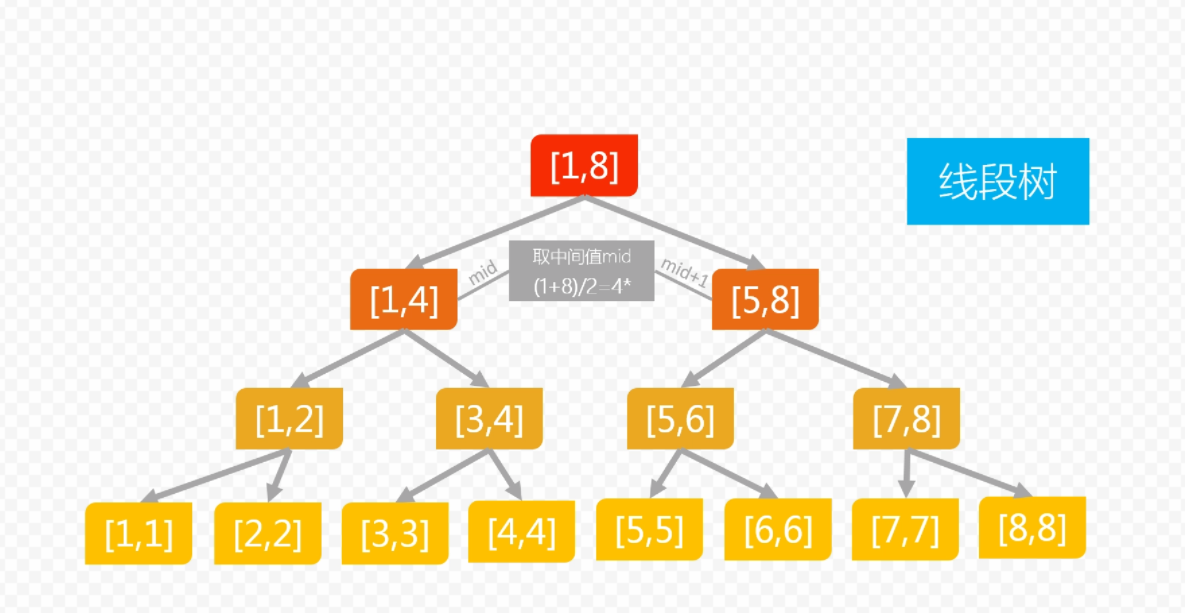
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,实际应用时一般还要开4N4N的数组以免越界,因此有时需要离散化让空间压缩。
线段树操作:1.单点修改
只要不断修改这个区间及其父区间即可,而不会影响其他区间情况,时间复杂度O(logn)
2.区间查询(最小值,最小值出现次数等某些)
比如要查询【2,5】这个区间,我们看看能不能将这个区间拆成线段树上的若干段区间。从根节点开始看,【2,5】与【1,7】没有什么关系,所以往下看,查询【2,5】与【1,4】的交【2,4】,查询【2,5】与【5,7】的交【5,5】,然后再继续往下递归,直到有满足的区间或者有孤立的节点了,然后再不断返回即可
例题:P3372 【模板】线段树 1
本题要进行区间加 和 区间查询操作, 其实这个树状数组改一改也能做,开两个树状数组就行了,这里采用线段树操作, 直接上板子。
#include <bits/stdc++.h>
using namespace std;
#define ll long long
typedef pair<int, int> PII;
#define pb push_back
const int N = 2E5 + 5;
int n, q, a[N];
const int mod = 1e9 + 7;
struct tag {
ll mul, add;
};
tag operator + (const tag &t1, const tag &t2) {
// (mul1 + add1) * mul2 + add2;
return {t1.mul * t2.mul , (t1.add * t2.mul % mod + t2.add)};
}
struct node {
tag t;
ll val;
int sz;
}seg[N * 4];
void update(int id) {
seg[id].val = (seg[id * 2].val + seg[id * 2 + 1].val);
}
void build(int id, int l, int r) {
seg[id].t = (tag){1, 0};
seg[id].sz = r - l + 1;
if(l == r){
seg[id].val = a[l];
} else {
int mid = (l + r) / 2;
build(id * 2, l, mid);
build(id * 2 + 1, mid + 1, r);
update(id);
}
}
void settag(int id, tag t) {
seg[id].val = seg[id].val * t.mul + seg[id].sz * t.add;
seg[id].t = seg[id].t + t;
}
void pushdown(int id) {
if(seg[id].t.mul != 1 || seg[id].t.add != 0) {
settag(id * 2, seg[id].t);
settag(id * 2 + 1, seg[id].t);
seg[id].t.mul = 1;
seg[id].t.add = 0;
}
}
void modify(int id, int l, int r, int ql, int qr, tag t) {
if(l == ql && r == qr) {
settag(id, t);
return;
}
pushdown(id);
int mid = (l + r) / 2;
if(qr <= mid) modify(id * 2, l, mid, ql, qr, t);
else if(ql > mid) modify(id * 2 + 1, mid + 1, r, ql, qr, t);
else modify(id * 2, l, mid, ql, mid, t),
modify(id * 2 + 1, mid + 1, r, mid + 1, qr, t);
update(id);
}
ll query(int id, int l, int r, int ql, int qr) {
if(l == ql && r == qr) {
return seg[id].val;
}
pushdown(id);
int mid = (l + r) / 2;
if(qr <= mid) return query(id * 2, l, mid, ql, qr);
else if(ql > mid) return query(id * 2 + 1, mid + 1, r, ql, qr);
else return (query(id * 2, l, mid, ql, mid) +
query(id * 2 + 1, mid + 1, r, mid + 1, qr));
}
int main(){
scanf("%d %d", &n, &q);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
build(1, 1, n);
while(q--) {
int ty; scanf("%d", &ty);
if(ty == 1) {
int l, r, d;
scanf("%d %d %d", &l, &r, &d);
modify(1, 1, n, l, r, (tag){1, d});
} else {
int l, r; scanf("%d %d", &l, &r);
printf("%lld\n", query(1, 1, n, l, r));
}
}
return 0;
}例题2:P3373 【模板】线段树 2
这里看到需要好多操作, 我们肯定要利用标记去做这些操作, 我们可以让标记记录 + 和 * 两种操作, 然后将所有的修改变成这俩个操作。 如:
-
将某区间每一个数乘上 x,那么就是*x + 0,
-
将某区间每一个数加上 x, 那么就是*0 + x;
-
求出某区间每一个数的和, 直接无脑query
-
#include <bits/stdc++.h> using namespace std; #define ll long long typedef pair<int, int> PII; #define pb push_back const int N = 2E5 + 5; int n, q, a[N]; const int mod = 1e9 + 7; struct tag { ll mul, add; }; tag operator + (const tag &t1, const tag &t2) { // (mul1 + add1) * mul2 + add2; return {t1.mul * t2.mul, (t1.add * t2.mul + t2.add)}; } struct node { tag t; ll val; int sz; }seg[N * 4]; void update(int id) { seg[id].val = (seg[id * 2].val + seg[id * 2 + 1].val); } void build(int id, int l, int r) { seg[id].t = (tag){1, 0}; seg[id].sz = r - l + 1; if(l == r){ seg[id].val = a[l]; } else { int mid = (l + r) / 2; build(id * 2, l, mid); build(id * 2 + 1, mid + 1, r); update(id); } } void settag(int id, tag t) { seg[id].val = seg[id].val * t.mul + seg[id].sz * t.add; seg[id].t = seg[id].t + t; } void pushdown(int id) { if(seg[id].t.mul != 1 || seg[id].t.add != 0) { settag(id * 2, seg[id].t); settag(id * 2 + 1, seg[id].t); seg[id].t.mul = 1; seg[id].t.add = 0; } } void modify(int id, int l, int r, int ql, int qr, tag t) { if(l == ql && r == qr) { settag(id, t); return; } pushdown(id); int mid = (l + r) / 2; if(qr <= mid) modify(id * 2, l, mid, ql, qr, t); else if(ql > mid) modify(id * 2 + 1, mid + 1, r, ql, qr, t); else modify(id * 2, l, mid, ql, mid, t), modify(id * 2 + 1, mid + 1, r, mid + 1, qr, t); update(id); } ll query(int id, int l, int r, int ql, int qr) { if(l == ql && r == qr) { return seg[id].val; } pushdown(id); int mid = (l + r) / 2; if(qr <= mid) return query(id * 2, l, mid, ql, qr); else if(ql > mid) return query(id * 2 + 1, mid + 1, r, ql, qr); else return (query(id * 2, l, mid, ql, mid) + query(id * 2 + 1, mid + 1, r, mid + 1, qr)); } int main(){ scanf("%d %d", &n, &q); for(int i = 1; i <= n; ++i) scanf("%d", &a[i]); build(1, 1, n); while(q--) { int ty; scanf("%d", &ty); if(ty <= 3) { int l, r, d; scanf("%d %d %d", &l, &r, &d); if(ty == 1) modify(1, 1, n, l, r, (tag){1, d}); else if (ty == 2) modify(1, 1, n, l, r, (tag){d, 0}); else modify(1, 1, n, l, r, (tag){0, d}); } else { int l, r; scanf("%d %d", &l, &r); printf("%lld\n", query(1, 1, n, l, r)); } } return 0; }




![[计算机网络]第一章 概述 -- 1.1 计算机网络在信息时代中的作用 1.2 互联网概述](https://img-blog.csdnimg.cn/29846eee2f384b83ab7db82be0d8acbf.png)