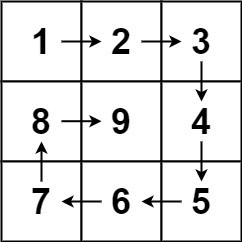
1.数字三角形（方向次数限制，动态规划）

  //如果n为奇数时，最后必然走到最后行最中间的数，如果为偶数，则取中间两个数的最大值，
  //因为向左下走的次数与向右下走的次数相差不能超过 1

#include <iostream>
using namespace std;
const int N=110;
int g[N][N];
int f[N][N];
int n;
int ans;
int main()
{
  cin>>n;
  for(int i=1;i<=n;i++)
  {
    for(int j=1;j<=i;j++)
    {
      cin>>g[i][j];
    }
  }
  for(int i=1;i<=n;i++)
  {
    for(int j=1;j<=i;j++)
    {
      f[i][j]=max(f[i-1][j],f[i-1][j-1])+g[i][j];
    }
  }
  //如果n为奇数时，最后必然走到最后行最中间的数，如果为偶数，则取中间两个数的最大值，
  //因为向左下走的次数与向右下走的次数相差不能超过 1
  if(n%2)cout<<f[n][n/2+1];
  else cout<<max(f[n][n/2],f[n][n/2+1]);
  return 0;
}

2.作物杂交（DFS，递归）

#include <iostream>
#include <map>
#include <vector>
using namespace std;
const int N=2000+100;
int n,m,k,t;
vector<pair<int,int>> fa[N];
int tim[N];
int f[N];//f[i]表示得到i需要花费的时间
map<int,int>mp;
int ans;
int dfs(int t)//倒着推
{
  for(int i=0;i<fa[t].size();i++)
  {
    int a=fa[t][i].first;
    int b=fa[t][i].second;
    if(!mp[a])dfs(a);
    if(!mp[b])dfs(b);
    if(mp[a]&&mp[b])
    {
      mp[t]=1;
      f[t]=min(f[t],max(tim[a],tim[b])+max(f[a],f[b]));
    }
  }
  return f[t];
}
int main()
{
  cin>>n>>m>>k>>t;
  for(int i=1;i<=n;i++)
  {
    cin>>tim[i];
    f[i]=1e9;//初始都是得不到的
  }
  for(int i=1;i<=m;i++)
  {
    int x;
    cin>>x;
    mp[x]=1;
    f[x]=0;//已经有了，得到的时间为0
  }
  for(int i=1;i<=k;i++)
  {
    int a,b,c;
    cin>>a>>b>>c;
    fa[c].push_back({a,b});
  }
  cout<<dfs(t);
  return 0;
}

3.Excel地址（思维）

#include <iostream>
#include <vector>
using namespace std;
int main()
{
  long long n;
  cin>>n;
  vector<char>v;
  while(n)
  {
    n--;//0-25表示A-Z，所以先减一
    v.push_back(n%26+'A');//贡献当前位的表示
    n/=26;//贡献当前位的权
  }
  for(int i=v.size()-1;i>=0;i--)
  cout<<v[i];
  return 0;
}

4.k倍区间（思维）

组合求法，假设%k值相等的区间有n个，根据得出的结论发现任何两个前缀区间的和对k取模的值相等，则由大的前缀区间减掉小的前缀区间所形成的区间的必定是K倍区间。那n个中取任何两个区间都可以组成k倍区间，问有多少k倍区间，就转换成n个区间取两个的情况有多少个，就是Cn2=n*(n-1)/2，所以对于每个%k值相等的区间都添加一次组合就可以算出总共有多少k倍区间了

#include <iostream>
using namespace std;
const int N=1e5+10;
#define ll long long
ll sum;
ll cnt[N];//cnt[i]表示与k取模后余i的个数
int a[N];
int n,k;
ll ans;
int main()
{
  cin>>n>>k;
  for(int i=1;i<=n;i++)
  {
    cin>>a[i];
    sum=sum+a[i];//计算前缀和
    cnt[sum%k]++;//统计所有前缀和%k后的余数相同个数
  }
  //余数为0直接就是k的倍数l
  ans+=cnt[0];
  //剩下的余数相同的前缀和选2个相同的进行相减
  //即可得到一个子区间且和是k的倍数
  for(int i=0;i<k;i++)
  {
    //组合数cnt[i]个数选两个：C(n,2)=n*(n-1)/2
    //求得的组合数即所有组合即可贡献答案
    ans+=cnt[i]*(cnt[i]-1)/2;
  }
  cout<<ans<<endl;
  return 0;
}

（思路来自Moon） 

 5.包子凑数（动态规划）

#include <iostream>
using namespace std;
const int N=110;
const int M=1e4;
int n;
int a[N];
int f[M];//f[i]=0表示i个包子凑不出来，f[i]=1表示i个包子凑得出来
int gcd(int a,int b)//用来判断是否互质，若全不互质那肯定凑不出来无限个
{
  return b?gcd(b,a%b):a;
}
int main()
{
  cin>>n;
  for(int i=0;i<n;i++)
  {
    cin>>a[i];
  } 
  //求出数组a的最大公因数
  int g=gcd(a[0],a[1]);
  for(int i=2;i<n;i++)
  {
    g=gcd(g,a[i]);
  }
  //如果最大公因数大于1，肯定无法表示的有无限
  if(g>1)
  {
    cout<<"INF"<<endl;
  }
  else
  {
    int ans=0;
   f[0]=1;//0个包子肯定可以
   for(int i=0;i<n;i++)
   {
     for(int j=0;j+a[i]<M;j++)
     {
       if(f[j])
       {
         f[j+a[i]]=1;
       }
     }
   }
   for(int i=0;i<M;i++)
   {
     if(!f[i])
     {
       ans++;
     }
   }
   cout<<ans<<endl;
  }
  return 0;
}

7.分巧克力（二分）

以下是错误代码！！（注意切巧克力是有边的限制的，不能使用面积，面积满足但是形状不满足的巧克力是不合法的！！） 

#include <iostream>
#include <cmath>
using namespace std;
const int N=1e5+10;
#define ll long long
int n,k;
int b=1e9;
int cnt=0;
ll sum[N]; 
int main()
{
  cin>>n>>k;
  for(int i=1;i<=n;i++)
  {
    int h,w;
    cin>>h>>w;
    int kk=(int)sqrt(h*w);
    b=min(b,kk);
    sum[i]=(ll)h*w;
  }
  for(int i=1;i<=n;i++)
  {
    cnt+=(sum[i]/(b*b));
  }
  if(cnt>=k)
  cout<<b<<endl;
  else
  {
    while(cnt<k)
    {
      b--;
      cnt=0;
      for(int i=1;i<=n;i++)
      {
        cnt+=(sum[i]/(b*b));
      }
    }
    cout<<b<<endl;
  }
  return 0;
}

#include <iostream>
#include <cmath>
using namespace std;
const int N=1e5+10;
#define ll long long
int n,k;
int ans;
int h[N],w[N];
bool check(int x)
{
  int cnt=0;
  for(int i=1;i<=n;i++)
  {
    cnt+=(h[i]/x)*(w[i]/x);//有多少个x的高，多少个x的宽，这样才能切出巧克力
  }
  return cnt>=k;
}
int main()
{
  cin>>n>>k;
  for(int i=1;i<=n;i++)
  {
    cin>>h[i]>>w[i];
  }
  int l=1;
  int r=N;
  while(l<=r)
  {
    int mid=(l+r)/2;
    if(check(mid))
    {
      ans=mid;//ans是符合要求的，不断取大的
      l=mid+1;
    }
    else
    {
      r=mid-1;
    }
  }
  cout<<ans<<endl;
  return 0;
}

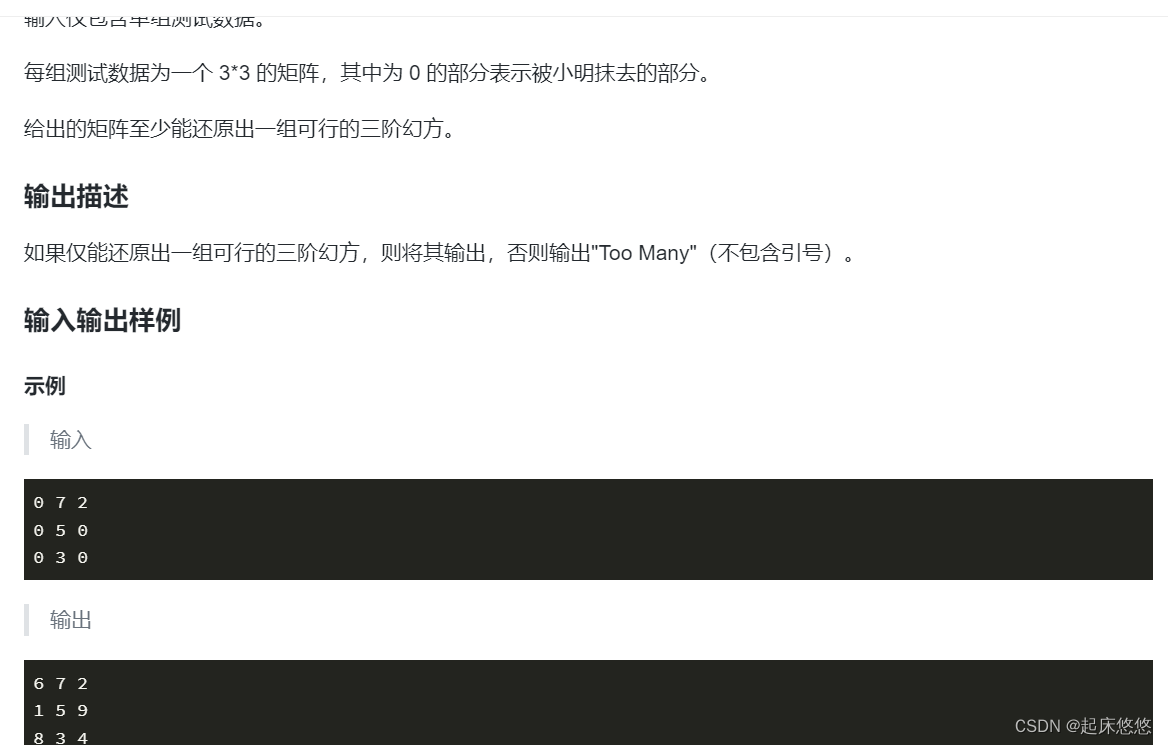
8.九宫幻方（DFS）

#include <iostream>
#include <map>
using namespace std;
int a[4][4];
int ans[4][4];
int n,cnt;
pair<int,int>p[10];
map<int,int>mp;
bool check()
{
  int sum=a[1][1]+a[2][2]+a[3][3];
  if(sum!=a[1][3]+a[2][2]+a[3][1])return 0;
  for(int i=1;i<=3;i++)
  {
    int temp1=0,temp2=0;
    for(int j=1;j<=3;j++)
    {
      temp1+=a[i][j];
      temp2+=a[j][i];
    }
    if(temp1!=sum||temp2!=sum)return 0;
  }
  return 1;
}
void dfs(int now)
{
  if(now>n)//也就是所有为0的点都已经遍历完了
  {
    if(check())
    {
      cnt++;
      for(int i=1;i<=3;i++)
      {
        for(int j=1;j<=3;j++)
        {
          ans[i][j]=a[i][j];
        }
      }
    }
    return;
  } 
  //x和y表示可以填数的点
  int x=p[now].first,y=p[now].second;
  for(int i=1;i<=9;i++)
  {
    if(mp[i])continue;//填过的不可以再填
    a[x][y]=i;
    mp[i]=1;
    dfs(now+1);
    a[x][y]=0;
    mp[i]=0;
  }
}
int main()
{
  for(int i=1;i<=3;i++)
  {
    for(int j=1;j<=3;j++)
    {
      cin>>a[i][j];
      if(!a[i][j])p[++n]=make_pair(i,j);
      mp[a[i][j]]=1;
    }
  }
  dfs(1);
  if(cnt==1)
  {
    for(int i=1;i<=3;i++)
    {
      for(int j=1;j<=3;j++)
      {
        cout<<ans[i][j]<<" \n"[j==3];
      }
    }
  }
  else cout<<"Too Many\n";
  return 0;
}