⭐每天一道leetcode：69.x的平方根（简单；不使用sqrt函数）

news2024/11/15 3:30:16

⭐今日份题目

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例1

输入：x = 4
输出：2

示例2

输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。

提示

0 <= x <= 2^31 - 1

⭐题目思路

还是先提取一下题目特征点：

算术平方根
取整
不得使用内置函数和算符

思路一——袖珍计算器算法（数学替换法）

「袖珍计算器算法」是一种用指数函数 exp 和对数函数 ln 代替平方根函数的方法。我们通过有限的可以使用的数学函数，得到我们想要计算的结果。

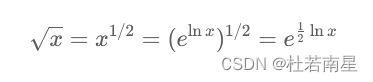
这样我们就可以得到根号下x 的值了。

代码

class Solution 
{
public:
    int mySqrt(int x) 
    {
        if(x==0) return 0;
        int ans=exp(0.5*log(x));
        return ((long long)(ans+1)*(ans+1)<=x?ans+1:ans);//判断ans+1和ans究竟谁是正确答案
    }
};

思路二——二分查找

由于我们最后只需要返回整数部分，所以我们只要找到满足ans*ans<=x的最大ans值即可，那么我们可以通过二分查找的方法来找它。

代码

class Solution 
{
public:
    int mySqrt(int x) {
        int l=0,r=x,ans=-1;
        while(l<=r) 
        {
            int mid=(l+r)/2;
            if((long long)mid*mid<=x&&(long long)(mid+1)*(mid+1)>x) 
            {
                ans=mid;
                break;
            }
            else if ((long long)mid*mid<=x) 
            {
                l=mid+1;
            } 
            else 
            {
                r=mid-1;
            }
        }
        return ans;
    }
};

这个方法的时间复杂度要高一些，但可以看到的是，内存消耗相比之下小了很多。