数学三角形

思路：就是下一层通过上一层的条件转移过来，注意数可以是负数，所以边界得取-INF，这样求上层 max 的时候不会被初始化的数如 0 影响。

#include<bits/stdc++.h>
using namespace std;

int n;
int a[505][505];
const int INF = 0x3f3f3f3f;
int main( ){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=0;j<=i+1;j++){
            if(j==0||j==i+1)a[i][j]=-INF;
            else{
                cin>>a[i][j];
                a[i][j]+=max(a[i-1][j],a[i-1][j-1]);
            }
        }
    }
    int res=-INF;
    for(int i=1;i<=n;i++){
        res=max(res,a[n][i]);
    }
    cout<<res<<'\n';
    return 0;
}

最长上升子序列

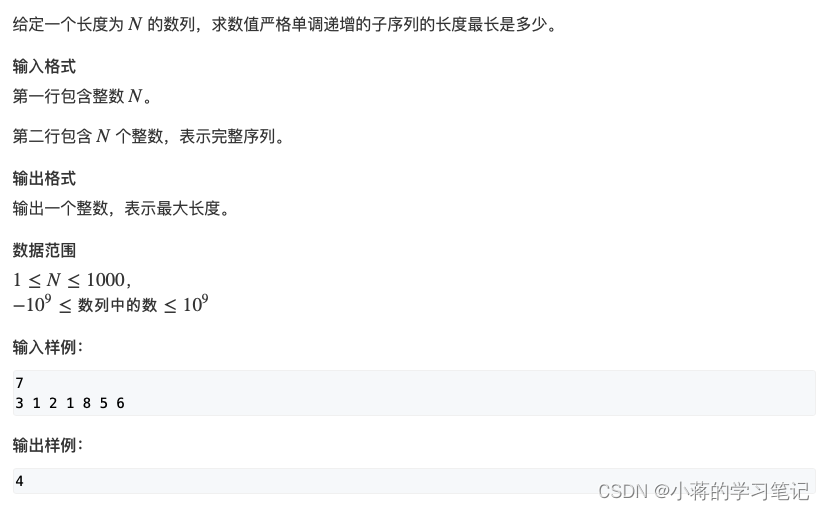
思路：dp[i]表示以 a[i]结尾的数的上升子序列的最大长度，他的初始化是 dp[i]=1，递推公式是 if(a[j]<a[i])dp[i] = max(dp[i],dp[j]+1)，可以打印看 dp 结果，最后是 max(result,dp[i])，dp[n-1]不一定是结果。注意遍历顺序，i 只能从小到大，j 前后顺序都可以。

#include<bits/stdc++.h>
using namespace std;
int n;
const int N = 1e3+10;
int a[N];
int dp[N];

int main( ){
    cin>>n;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int i=0;i<n;i++)dp[i]=1;
    for(int i=1;i<n;i++){
        for(int j=0;j<=i;j++){
            if(a[j]<a[i])dp[i]=max(dp[j]+1,dp[i]);
        }
    }
    int result = 0;
    for(int i=0;i<n;i++)
        result = max(result,dp[i]);
    cout<<result<<'\n';
    return 0;
}