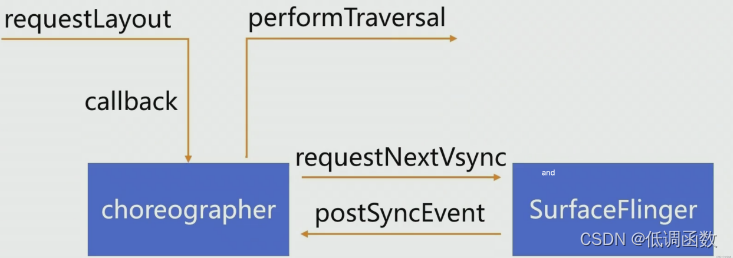
矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
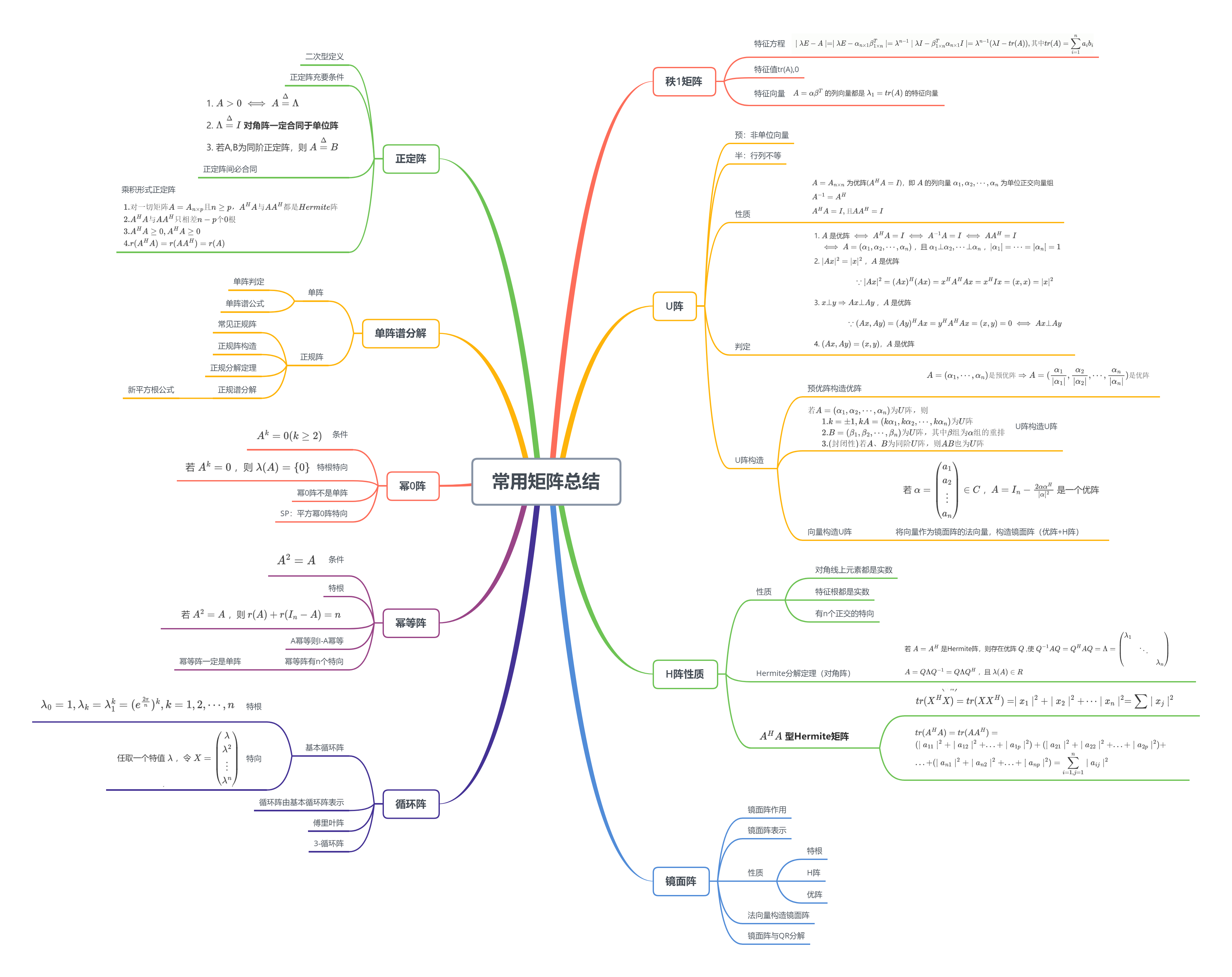
8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
8. 常用矩阵总结——镜面阵，正定阵
8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

---

8.6 单阵

2. 矩阵分解——单阵谱分解

2. 矩阵分解——正规分解——正规阵

8.7 幂0阵

8.7.1 条件

$A^k=0(k\ge 2)$ ，且 $A\ne 0$ ，则为 $k$ 次幂0阵

• 若 $(A-bI{)}^k=0$ ，$A\ne bI$ ，则 $A$ 为平移幂0阵

8.7.2 特根特向

若 $A^k=0$ ，则 λ ( A ) = { 0 } \lambda(A)=\{0\} λ(A)={0}

• 由 Cayley 定理，${\lambda }^k=0\Rightarrow \lambda =0$
• 由特向(4.1)求法，$A\cdot A=0$ ，则 $A$ 中各列都是0根的特向

若 ( A − b I ) k = 0 ⇒ λ ( A ) = { b , ⋯   , b } (A-bI)^k=0\Rightarrow \lambda(A)=\{b,\cdots,b\} (A−bI)k=0⇒λ(A)={b,⋯,b}

8.7.3 幂0阵不是单阵

$$\begin{array}{rl}& 设A^k=0(A\ne 0)，假设A为单阵，\Rightarrow P^{-1}AP\stackrel{相似}{=}D=\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_n\end{array}\right)=0\\ & 与A\ne 0矛盾，故A为幂0阵，则非单阵\end{array}$$

推论：$A$ 与 $A-bI$ 同为单阵或非单阵，则 平移不改变单阵或非单阵

• 若 $(A-bI{)}^k=0$ 且 $A-bI\ne 0$ 则A非单阵 ，且 λ ( A ) = { b , b , ⋯   , b } \lambda(A)=\{b,b,\cdots,b\} λ(A)={b,b,⋯,b}

  则 $f(A)=f(b)I+\frac{f^{\prime }(b)}{1!}(A-bI)+\frac{f^{\prime \prime }(b)}{2!}(A-bI{)}^2+\cdots \frac{f^{k-1}(b)}{(k-1)!}(A-bI{)}^{k-1}$ 为 $f(x)$ 的解析式

8.7.4 记忆：平方幂0

若 $A^2=0(A\ne 0)$ ，则A中列都是0根特向

• A中列 $\left(\begin{array}{c}1\\ -1\end{array}\right),\left(\begin{array}{c}1\\ 1\end{array}\right)$ 为 $\lambda =0$ 的特向

eg
$$A=\left(\begin{array}{cc}3& 1\\ -1& 1\end{array}\right)$$

A − 2 I = ( 1 1 − 1 − 1 ) , 则 0 为 A − 2 I 的特根，其特向为 ( 1 1 ) , ( 1 − 1 ) ⇒ A 的特向为 { 2 , 2 } , 其特向为 ( 1 1 ) , ( 1 − 1 ) \begin{aligned} &A-2I=\left( \begin{matrix} 1&1\\-1&-1 \end{matrix} \right),则0为A-2I的特根，其特向为\left(\begin{matrix}1\\1\end{matrix}\right),\left(\begin{matrix}1\\-1\end{matrix}\right) \\ &\Rightarrow A的特向为\{2,2\},其特向为 \left(\begin{matrix}1\\1\end{matrix}\right),\left(\begin{matrix}1\\-1\end{matrix}\right) \end{aligned} ​A−2I=(1−1​1−1​),则0为A−2I的特根，其特向为(11​),(1−1​)⇒A的特向为{2,2},其特向为(11​),(1−1​)​

8.8 幂等阵性质

幂等条件：$A^2=A$

特根：$\lambda (A)=1或0$
由 C a y l e y 定理， λ 2 = λ ⇒ λ = 1 或 0 , 可写全体特根 λ ( A ) = { 1 , ⋯   , 1 ⏟ ( r ) 个 1 , 0 , ⋯   , 0 ⏟ ( n − r ) 个 0 } \begin{aligned} &由Cayley定理，\lambda^2=\lambda\Rightarrow \lambda=1或0,可写全体特根\lambda(A)=\{\underbrace{1,\cdots,1}_{(r)个1},\underbrace{0,\cdots,0}_{(n-r)个0}\} \end{aligned} ​由Cayley定理，λ2=λ⇒λ=1或0,可写全体特根λ(A)={(r)个1 1,⋯,1​​,(n−r)个0 0,⋯,0​​}​

8.8.1 幂等阵一定为单阵(相似于对角阵)

$A\sim D=\left(\begin{array}{cccccc}1& & & & & \\ & \ddots & & & & \\ & & 1& & & \\ & & & 0& & \\ & & & & \ddots & \\ & & & & & 0\end{array}\right)$

单阵引理：

• $f(x)$ 为A的0化式，若 $f(A)=0$ ,且f(x)无重根，则A为单阵
  $$\begin{array}{rl}& 若A^2=A\Rightarrow A^2-A=0或A(A-I)=0,则A有0化式f(x)=x^2-x，无重根,故A为单阵\end{array}$$

8.8.2 r(A)与r(I-A)关系

若 $A^2=A$ ，则 $r(A)+r(I_n-A)=n$
$$\begin{array}{rl}& 由于A(A-I)=0\Rightarrow r(A)+r(A-I)\le n⟺r(A)+r(I_n-A)\le n\\ & 又I=A+(I-A)，n=r(I)=r(A+(I-A))\le r(A)+r(I-A)\le n\\ & \therefore r(A)+r(I_n-A)=r(A)+r(A-I_n)=n\end{array}$$

8.8.3 A幂等$⟺$ I-A幂等

$A^2=A⟺(I-A{)}^2=(I-A)$

• 则有 $tr(I-A)=tr(I)-tr(A)=n-r=r(I-A)$

证明：
$$\begin{array}{rl}& A^2=A\Rightarrow (I-A{)}^2=I^2-2A+A^2=I-A\end{array}$$

8.8.4 幂等阵的特向

A是幂等阵，则 $A$ 有 $n$ 个无关特向
$$\begin{array}{rl}& 设特根0的特向为X_0,A{X}_0=0,则齐次方程线性无关解的个数为n-r(A)\\ & 设特根1的特向为X_1,A{X}_1=X_1⟺(A-I)X_1=0，则齐次方程线性无关解的个数为n-r(I-A)=r(A)\\ & 故特向有n个\end{array}$$

8.8.5 谱分解中谱阵为幂等阵

谱分解 $A={\lambda }_1{G}_2+\cdots +{\lambda }_k{G}_k$ 中 $G_i$ 为幂等阵（$G_1^2=G_1,\cdots ,G_k^2=G_k$

8.9 循环矩阵

$n$ 阶循环阵定义为：$C=[c_0,c_1,\cdots ,c_{n-1}]\left(\begin{array}{ccccc}{c}_0& c_1& c_2& \cdots & c_{n-1}\\ c_{n-1}& c_0& c_1& \cdots & c_{n-2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ c_1& c_2& c_3& \cdots & c_0\end{array}\right)$

8.9.1基本循环阵

$A=[1,0\cdots ,0]=\left(\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\\ 1& 0& 0& \cdots & 0\end{array}\right)\stackrel{按列}{=}(e_n,e_1,e_2,\cdots ,e_{n-1})\stackrel{按行}{=}\left(\begin{array}{c}{e}_2^H\\ e_3^H\\ ⋮\\ e_n^H\\ e_1^H\end{array}\right)$

a. $A$ 特根

由 A n = I ⇒ λ ( A n ) = { λ 1 n , λ 2 n , ⋯   , λ n n } = λ ( I ) = { 1 , 1 , ⋯   , 1 } A^n=I\Rightarrow\lambda(A^n)=\{\lambda_1^n,\lambda_2^n,\cdots,\lambda_n^n\}=\lambda(I)=\{1,1,\cdots,1\} An=I⇒λ(An)={λ1n​,λ2n​,⋯,λnn​}=λ(I)={1,1,⋯,1} ，有 ${\lambda }_1^n=1,{\lambda }_2^n=1,\cdots ,{\lambda }_n^n=1$

${\lambda }^n=1$ 的根恰是单位圆上的 $n$ 个分点，${\lambda }_0=1$ ，${\lambda }_1=e^{\frac{2\pi }{n}i}=\cos \frac{2\pi }{n}+isin\frac{2\pi }{n}$ ，${\lambda }_2=e^{\frac{2\pi }{n}2i}$ ，$\cdots$ ，${\lambda }_{n-1}=e^{\frac{2\pi }{n}(n-1)i}$

• ${\lambda }_0=1,{\lambda }_k={\lambda }_1^k=(e^{\frac{2\pi }{n}}{)}^k,k=1,2,\cdots ,n$

• ${\lambda }_k^n=1$

b. $A$ 的特向

任取一个特值 $\lambda$ ，令 $X=\left(\begin{array}{c}\lambda \\ {\lambda }^2\\ ⋮\\ {\lambda }^n\end{array}\right)$ ，$\Rightarrow AX=\left(\begin{array}{ccccc}0& 1& 0& \cdots & 0\\ 0& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & 1\\ 1& 0& 0& \cdots & 0\end{array}\right)\left(\begin{array}{c}\lambda \\ {\lambda }^2\\ ⋮\\ {\lambda }^{n-1}\\ {\lambda }^n\end{array}\right)=\left(\begin{array}{c}{\lambda }^2\\ {\lambda }^3\\ ⋮\\ {\lambda }^{n-1}\\ \lambda \end{array}\right)=\left(\begin{array}{c}{\lambda }^2\\ {\lambda }^3\\ ⋮\\ {\lambda }^{n-1}\\ {\lambda }^{n+1}\end{array}\right)=\lambda \left(\begin{array}{c}\lambda \\ {\lambda }^2\\ ⋮\\ {\lambda }^{n-1}\\ {\lambda }^n\end{array}\right)=\lambda X$

故取 ${\lambda }_0=1$ ，${\lambda }_1=e^{\frac{2\pi }{n}i}$ ，${\lambda }_2=e^{\frac{2\pi }{n}2i}$ ，$\cdots$ ，${\lambda }_{n-1}=e^{\frac{2\pi }{n}(n-1)i}$

令 $X_0=\left(\begin{array}{c}{\lambda }_0\\ {\lambda }_0^2\\ ⋮\\ {\lambda }_0^n\end{array}\right)=\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)$ ，$X_1=\left(\begin{array}{c}{\lambda }_1\\ {\lambda }_1^2\\ ⋮\\ {\lambda }_1^n\end{array}\right)$ ，$\cdots$ ，$X_{n-1}=\left(\begin{array}{c}{\lambda }_{n-1}\\ {\lambda }_{n-1}^2\\ ⋮\\ {\lambda }_{n-1}^n\end{array}\right)$

• 或可写作： $X_0=\left(\begin{array}{c}1\\ 1\\ ⋮\\ 1\end{array}\right)$ ，$X_1=\left(\begin{array}{c}1\\ {\lambda }_1\\ ⋮\\ {\lambda }_1^{n-1}\end{array}\right)=\left(\begin{array}{c}{\lambda }_1^n\\ {\lambda }_1\\ ⋮\\ {\lambda }_1^{n-1}\end{array}\right)$ ，$\cdots$ ，$X_{n-1}=\left(\begin{array}{c}1\\ {\lambda }_{n-1}\\ ⋮\\ {\lambda }_{n-1}^{n-1}\end{array}\right)=\left(\begin{array}{c}{\lambda }_{n-1}^n\\ {\lambda }_{n-1}\\ ⋮\\ {\lambda }_{n-1}^{n-1}\end{array}\right)$

$|X_0{|}^2=|X_1{|}^2=\cdots =|X_{n-1}{|}^2=n$ ，且 $X_0\perp X_1\perp \cdots \perp X_{n-1}$ ，$|X_j|=\sqrt{n}$

8.9.2 循环阵可由基本循环阵表示

• $A^0=(e_1,e_2,e_3,\cdots ,e_n)=I$
• $A^1=(e_n,e_1,e_2,\cdots ,e_{n-1})$
• $A^2=(e_{n-1},e_n,e_1,\cdots ,e_{n-2})$
• $A^{n-1}=(e_2,e_3,e_4,\cdots ,e_1)$
• $A^n=(e_1,e_2,e_3,\cdots ,e_n)$

令矩阵函数 $f(A)=c_{0}I+c_{1}A+c_2{A}_2+\cdots +c_{n-1}{A}^{n-1}=C$

• 可知基本循环阵 $A$ 正规 $\Rightarrow f(A)$ 正规，$C$ 正规
• $A$ 与 $f(A)$ 有相同特向， λ ( A ) = { λ 1 , λ 2 , ⋯   , λ n } \lambda(A)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\} λ(A)={λ1​,λ2​,⋯,λn​} ， λ ( f ( A ) ) = { f ( λ 1 ) , f ( λ 2 ) , ⋯   , f ( λ n ) } \lambda(f(A))=\{f(\lambda_1),f(\lambda_2),\cdots,f(\lambda_n)\} λ(f(A))={f(λ1​),f(λ2​),⋯,f(λn​)}

8.9.3 傅里叶阵

令 $Q=\left(\frac{X_0}{|X_0|},\frac{X_1}{|X_1|},\cdots ,\frac{X_{n-1}}{|X_{n-1}|}\right)=\frac{1}{\sqrt{n}}\left(X_0,X_1,\cdots ,X_{n-1}\right)$ 为优阵（傅里叶阵）

$\Rightarrow Q^{-1}AQ=Q^{H}AQ=D=\left(\begin{array}{cccc}{\lambda }_0& & & \\ & {\lambda }_1& & \\ & & \ddots & \\ & & & {\lambda }_{n-1}\end{array}\right)$

因为 $C=f(A)$ 与 $A$ 有相同的特向 ，有相同的优阵 $Q$

$\Rightarrow Q^{-1}CQ=Q^{-1}f(A)Q=Q^{H}f(A)Q=D=\left(\begin{array}{cccc}f({\lambda }_0)& & & \\ & f({\lambda }_1)& & \\ & & \ddots & \\ & & & f({\lambda }_{n-1})\end{array}\right)$

8.9.4 3-循环阵

求 3-循环阵 $A=[a_0,a_1,a_2]=\left(\begin{array}{ccc}{a}_0& a_1& a_2\\ a_2& a_0& a_1\\ a_1& a_2& a_0\end{array}\right)$ 的三个正交特征向量

令基本循环阵 $\Omega =(e_3,e_1,e_2)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right)$ ，有基本循环阵性质可知 ${\Omega }^3=I$ ，特根

λ ( Ω ) = { λ 1 , λ 2 , λ 3 } \lambda(\Omega)=\{\lambda_1,\lambda_2,\lambda_3\} λ(Ω)={λ1​,λ2​,λ3​} 为平面上单位圆周的三等分点，满足 ${\lambda }_1^3={\lambda }_2^3={\lambda }_3^3=1$

${\lambda }_j=e^{\frac{2\pi }{3}ji},j=1,2,3$

令 $X_j=\left(\begin{array}{c}{\lambda }_1\\ {\lambda }_1^2\\ {\lambda }_1^3\end{array}\right)$ ，可知 $\Omega X_j=\Omega \left(\begin{array}{c}{\lambda }_j\\ {\lambda }_j^2\\ {\lambda }_j^3\end{array}\right)=\left(\begin{array}{c}{\lambda }_j^2\\ {\lambda }_j^3\\ {\lambda }_j\end{array}\right)=\left(\begin{array}{c}{\lambda }_j^2\\ {\lambda }_j^3\\ {\lambda }_j^4\end{array}\right)={\lambda }_j\left(\begin{array}{c}{\lambda }_j\\ {\lambda }_j^2\\ {\lambda }_j^3\end{array}\right)={\lambda }_j{X}_j$

即 $X_j$ 是属于 ${\lambda }_j$ 的 $\Omega$ 的特向，故 $\Omega$ 恰有3个特向 $X_1,X_2,X_3$ 且 $X_1\perp X_2\perp X_3$ ，$|X_1|=|X_2|=|X_3|=\sqrt{3}$

令优阵 $Q=(q_1,q_2,q_3)=\left(\frac{X_1}{|X_1|},\frac{X_2}{|X_2|},\frac{X_3}{|X_3|}\right)=\frac{1}{\sqrt{3}}\left(\begin{array}{ccc}{\lambda }_1& {\lambda }_2& {\lambda }_3\\ {\lambda }_1^2& {\lambda }_2^2& {\lambda }_3^2\\ {\lambda }_1^3& {\lambda }_2^3& {\lambda }_3^3\end{array}\right)$ (为傅里叶优阵)

可得优分解 $Q^{-1}\Omega Q=D\left(\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right)$ ，其中 $\Omega =(e_3,e_1,e_2)=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right)$

• 或者 $Q=\frac{1}{\sqrt{3}}\left(\begin{array}{ccc}1& 1& 1\\ {\lambda }_1& {\lambda }_2& {\lambda }_3\\ {\lambda }_1^2& {\lambda }_2^2& {\lambda }_2^2\end{array}\right)$ ， $\Omega =\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 1& 0& 0\end{array}\right)$ 特向 $\left(\begin{array}{c}1\\ {\lambda }_1\\ {\lambda }_1^2\end{array}\right),\left(\begin{array}{c}1\\ {\lambda }_2\\ {\lambda }_2^2\end{array}\right),\left(\begin{array}{c}1\\ {\lambda }_3\\ {\lambda }_3^2\end{array}\right)$

  优分解 $Q^{-1}\Omega Q=D=\left(\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & {\lambda }_3\end{array}\right)$

可写 3-循环阵 $A=[a_0,a_1,a_2]=\left(\begin{array}{ccc}{a}_0& a_1& a_2\\ a_2& a_0& a_1\\ a_1& a_2& a_0\end{array}\right)=a_{0}I+a_1\Omega +a_2{\Omega }^2$