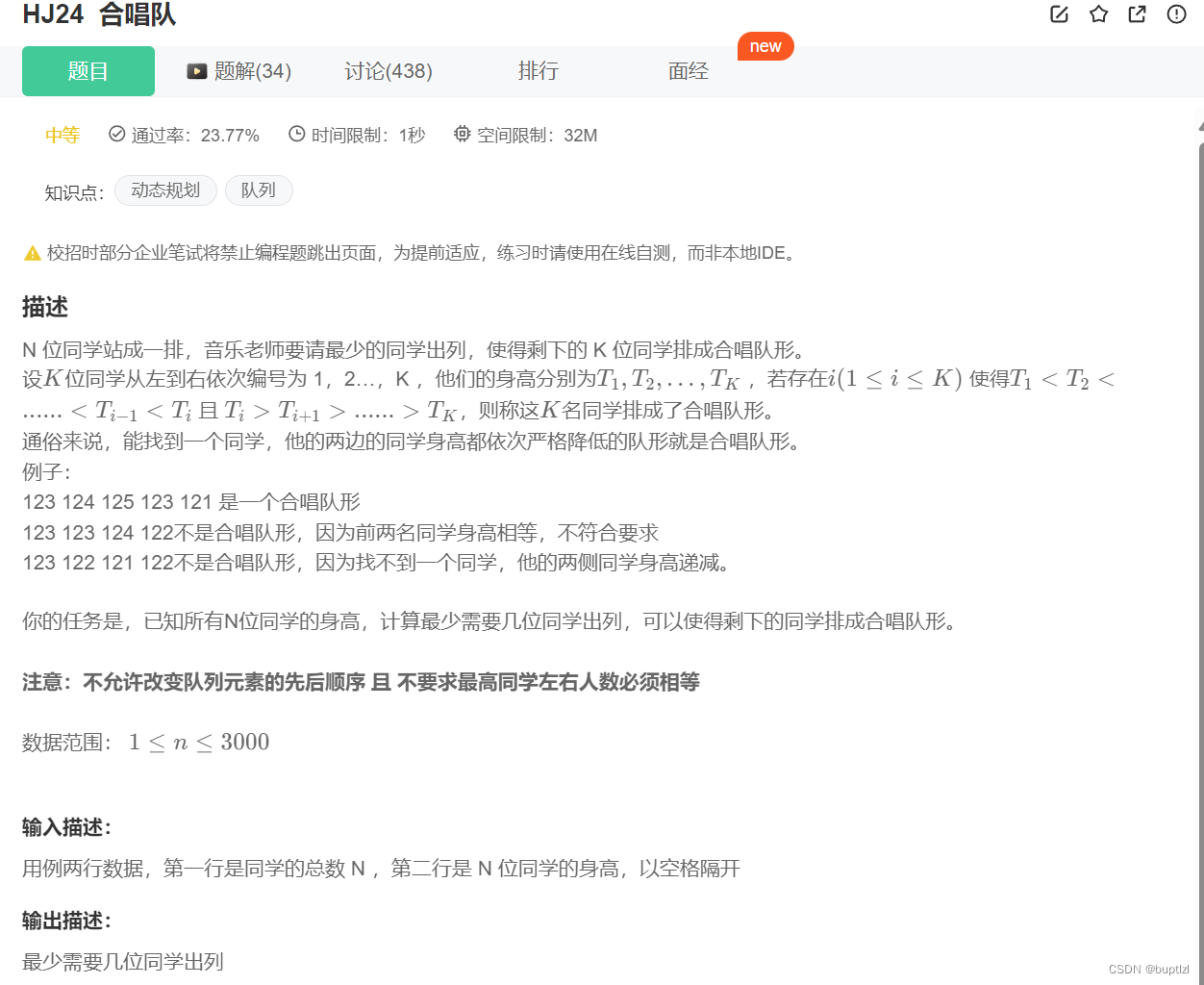
本题抽象出来，我们需要找到最长递增子序列，还需要一个最长递减子序列，然后两个子序列的长度相加减去1就是我们这个合唱队的最大长度。然后我们用所有的人数减去合唱队最大长度，就是我们要求的最少需要几位同学出列。

这个题和上一题求最长递增子序列类似，只不过是又求了一个递减子序列，然后进行运算即可。

我们仍采用动态规划来解决。dp[i]表示包含nums[i]在内的最长递增子序列的长度。在本题中我们需要两个，以left和right区分。比如我们找到nums[i]此时left[i]+right[i]最大，就是表示以nums[i]为中心，其左右两侧满足递增递减并且整个序列长度最大。

先找到左侧的left最长递增子序列的长度。整个left[]应该初始化为1。因为最小递增子序列就是只包含其本身这个元素，所以是1。当nums[i]>nums[j]的时候（i>j），此时表示dp[i] = Math.max(dp[i],dp[j]+1)（dp就是left）。然后我们得到left数组。

同理，我们找递减的数组，right，如果我们从后往前遍历，就是在找递增的子序列，就和left的逻辑一致了。所以，我们从后往前遍历，并且right也都初始化为1。当nums[i]>numsj。此时满足递减的条件，所以right[i] = Math.max(right[i],right[j]+1)。

然后我们得到了right和left两个数组，此时我们要找到最大的合唱队长度，就是将right和left相加，找到结果最大的值（表示此时以nums[i]为中心，能够建立起最长的合唱队），但我们多加了一个i，因为right和left都包括了nums[i]，所以我们要减去1才可以。

然后我们用整体的人数减去我们得到的最大值，就得到了我们要求的出列的最少人数。

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt();
            int[] arr = new int[n];
            for (int i = 0; i < n; i++) {
                arr[i] = sc.nextInt();
            }

            int[] left = new int[n]; //存储每个数左边小于其的数的个数
            int[] right = new int[n];//存储每个数右边小于其的数的个数
            left[0] = 1;            //最左边的数设为1
            right[n - 1] = 1;        //最右边的数设为1
            //计算每个位置左侧的最长递增
            for (int i = 0; i < n; i++) {
                left[i] = 1;
                for (int j = 0; j < i; j++) {
                    if (arr[i] > arr[j]) {   //动态规划
                        left[i] = Math.max(left[j] + 1, left[i]);
                    }
                }
            }
            //计算每个位置右侧的最长递减
            for (int i = n - 1; i >= 0; i--) {
                right[i] = 1;
                for (int j = n - 1; j > i; j--) {
                    if (arr[i] > arr[j]) {   //动态规划
                        right[i] = Math.max(right[i], right[j] + 1);
                    }
                }
            }
            // 记录每个位置的值
            int[] result = new int[n];
            for (int i = 0; i < n; i++) {
                //位置 i计算了两次 所以需要－1
                result[i] = left[i] + right[i] - 1; //两个都包含本身
            }

            //找到最大的满足要求的值
            int max = 1;
            for (int i = 0; i < n; i++) {
                max = Math.max(result[i],max);
            }
            System.out.println(n - max);
        }

    }
}