差分的基本思想详情见博客（一维、二维差分）：
https://blog.csdn.net/weixin_45629285/article/details/111146240

算法分析：

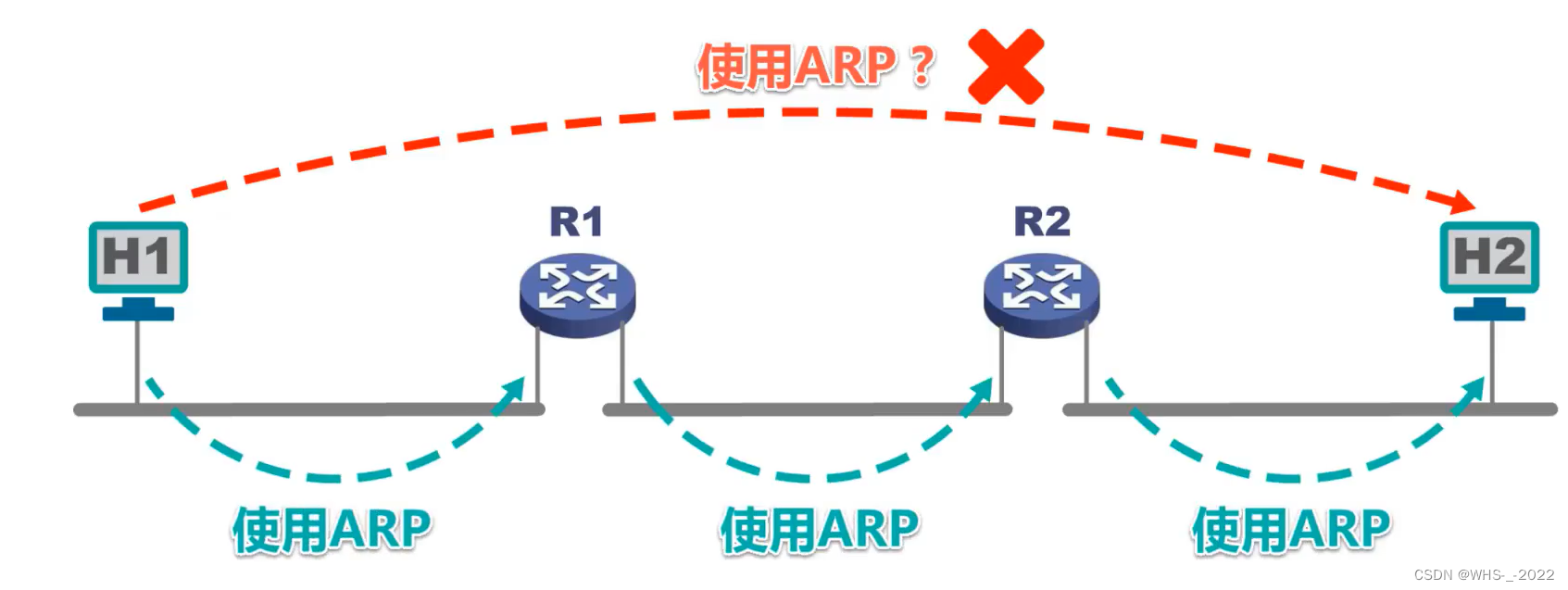
面向的对象可以是树上的结点，也可以是树上的边
结点表述方式：
问题：
给定一棵有N个点的树，所有节点的权值初始时都为0。
有K次操作，每次指定两个点s,t，将s到t路径上所有点的权值都+c，求最后树上每个结点的权值。

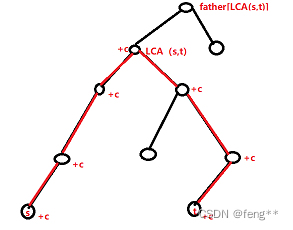
求解思路：
对于每一次修改s,t，将s,t的权值+c;
将LCA(s,t)和father[LCA(s,t)]的权值-c;
K次操作后每个结点最终被覆盖的次数（最终的权值）就是这个点所在子树的权值和。

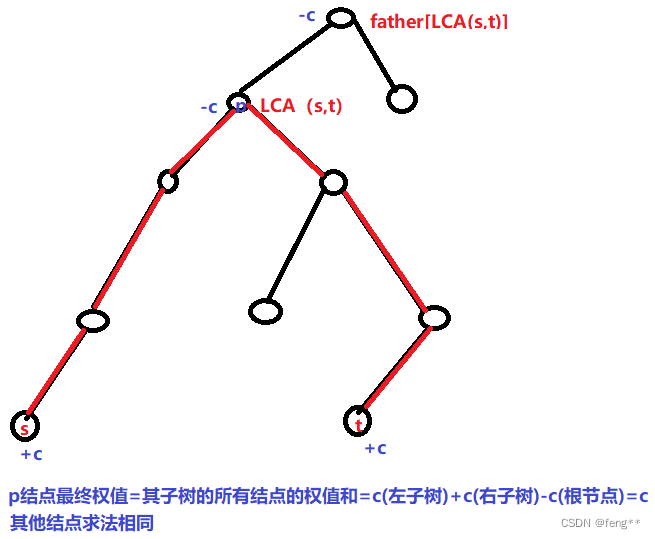
边表述方式：
问题：
给定一棵有N个点的树，或者为有N-1条边将任意两个点通过路径连接起来的无向图，所有边的权值初始时都为0。
有K次操作，每次指定两个点s,t，将s到t路径上所有边的权值都+c，求最后树上每个边的权值。

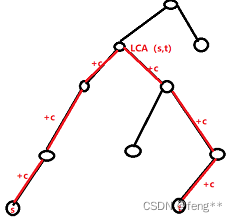
求解思路：
对于每一次修改结点s,t，将s,t的权值+c;
将LCA(s,t)的权值-2*c;
K次操作后每个边最终被覆盖的次数（最终的权值）就是这个边下面的结点所在子树的权值和。

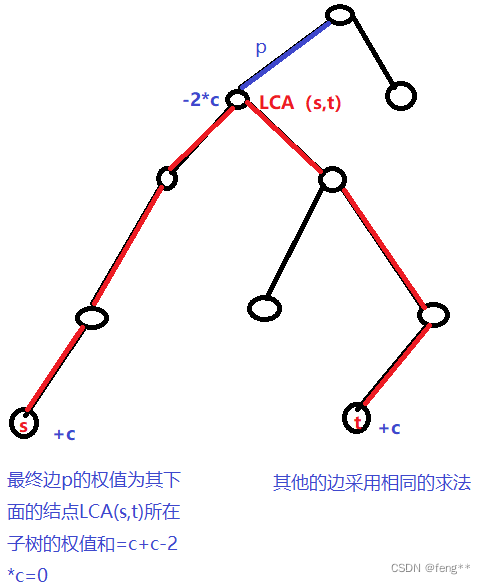
注意，两种方式的表示方法的求解思路有一点小的不同，但是我们只要保证一个思想，就是需要增加的才增加，不需要改变的就要减去
其中求LCA有三种方法：向上标记法、倍增法和tarjan离线算法，具体参考博客：https://blog.csdn.net/m0_58642116/article/details/128550161?spm=1001.2014.3001.5501

练习例题

链接：
https://www.acwing.com/problem/content/description/354/
分析：
1.主要边就构成了一棵树，附加边其实就是非树边，读题的时候就要能读出来，转化一下意思
2.一个附加边如果与一些主要边组成了环，这个环上的所有主要边砍断的同时也需要砍断这个附加边，也就相当于这些主要边砍断树的可能性都加一；如果主要边没有跟附加边组成环，那直接砍断这个主要边就能使得图不连通；但是如果主要边与多个附加边组成了环，砍断了当前主要边，再砍一个附加边没法使图不连通
3.最终也就是转化为了树上两个结点之间路径的问题，转化为树上差分问题
任意一个附加边，将附加边两端结点(s,t)间的树边的权值都加一，也就是s权值+1，t权值+1，LCA(s,t)-2；
AC代码：

#include<iostream>
#include<vector>
#include<queue>
#include<string.h>
using namespace std;
const int INF=0x3f3f3f3f;
int n,m,u,v,ans=0;
const int N=100005;
vector<int>tr[N]; 
int depth[N],fa[N][17];
int wei[N];  //树中每个结点的权值 

void bfs(int s)
{
	queue<int>que;
	memset(depth,INF,sizeof(depth));
	que.push(s);
	depth[0]=0;depth[1]=1;
	while(!que.empty())
	{
		int u=que.front();
		que.pop();
		
		for(int i=0;i<tr[u].size();i++)
		{
			int v=tr[u][i];
			if(depth[v]==INF)
			{
				depth[v]=depth[u]+1;
				que.push(v);
				
				fa[v][0]=u;
				for(int k=1;k<=16;k++)
				{
					fa[v][k]=fa[fa[v][k-1]][k-1]; 
				} 
			}
		}
	}
}
int LCA(int x,int y)
{
	if(depth[x]<depth[y]) swap(x,y);
	for(int k=16;k>=0;k--)
	{
		if(depth[fa[x][k]]>=depth[y])
		{
			x=fa[x][k];
		}
	}
	if(x==y) return x;
	for(int k=16;k>=0;k--)
	{
		if(fa[x][k]!=fa[y][k])
		{
			x=fa[x][k];
			y=fa[y][k];
		}
	}
	return fa[x][0];
} 

int dfs(int s,int fa)
{
	//以s为根节点的子树的权值 
	int num=0;
	for(int i=0;i<tr[s].size();i++)
	{
		if(tr[s][i]==fa) continue;
		num+=dfs(tr[s][i],s);
	}
	
	//再加上边下面的这个结点的权值（当前子树根节点权值） 
	num+=wei[s];
	
	if(s==1)  return num;  //跟结点上面的那个边不存在，直接返回 
	
	if(num==0)  ans+=m;   //当前主要边（树边）没有与任何附加边（非树边）组成环，直接砍断就能使得图分成两半，附加边就随便砍哪条都行 
	else if(num==1) ans+=1;   //当前主要边与一条 附加边组成环，要想使得图不连通砍断这个边的同时还要砍断那条附加边 
	//num>=2时，主要边与多个附加边组成了环，砍断了当前主要边，再砍一个附加边没法使图不连通 
	return num;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<n;i++)
	{
		cin>>u>>v;
		tr[u].push_back(v);
		tr[v].push_back(u);
	}
	bfs(1);  //倍增法初始化depth、fa数组
	
	//直接输入遍历非树边(附加边)
	for(int i=0;i<m;i++)
	{
		cin>>u>>v;
		int lca=LCA(u,v);
	//	cout<<lca<<endl;
		wei[u]+=1;  //差分求权值
		wei[v]+=1;
		wei[lca]-=2;
	} 
	//遍历整棵树差分法求每条边的权值，并对树边进行讨论求方法数
	dfs(1,-1);
	cout<<ans<<endl;
	return 0;
}