9. 回文数，10. 正则表达式匹配，11. 盛最多水的容器，每题做详细思路梳理，配套Python&Java双语代码， 2024.03.08 可通过leetcode所有测试用例。

目录

9. 回文数

解题思路

完整代码

Java

Python

10. 正则表达式匹配

解题思路

完整代码

Java

Python

11. 盛最多水的容器

解题思路

完整代码

Java

Python

---

9. 回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数
是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。
 

示例 1：

输入：x = 121
输出：true
示例 2：

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3：

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

解题思路

1. 负数和末尾为0的情况：负数不是回文数。除了0以外，任何末尾为0的数也不可能是回文数，因为回文数的起始数字不能为0。
2. 反转一半数字：为了避免反转整个数字可能导致的整数溢出问题，我们只反转整数的一半。当反转的一半数字大于或等于剩余的一半数字时，就意味着已经处理了一半以上的数字。

完整代码

Java

public class Solution {
    public boolean isPalindrome(int x) {
        if (x < 0 || (x % 10 == 0 && x != 0)) {
            return false;
        }

        int reversedHalf = 0;
        while (x > reversedHalf) {
            reversedHalf = reversedHalf * 10 + x % 10;
            x /= 10;
        }

        // 当数字长度为偶数时，原始数字的一半应该等于反转后的一半数字；
        // 当数字长度为奇数时，去掉反转一半的末位数字（通过/10操作）后，应该等于原始数字的一半。
        return x == reversedHalf || x == reversedHalf / 10;
    }
}

Python

class Solution:
    def isPalindrome(self, x: int) -> bool:
        # 负数或者末尾为0（但不是0本身）的数不是回文数
        if x < 0 or (x % 10 == 0 and x != 0):
            return False

        reversed_half = 0
        while x > reversed_half:
            reversed_half = reversed_half * 10 + x % 10
            x //= 10

        # 对于偶数长度的数字，反转的一半应该等于剩余的一半。
        # 对于奇数长度的数字，去掉反转一半的末位数字（通过//10操作）后，应该等于剩余的一半。
        return x == reversed_half or x == reversed_half // 10

10. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

 
示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。
示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。
示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。
 

提示：

1 <= s.length <= 20
1 <= p.length <= 20
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母，以及字符 . 和 *。
保证每次出现字符 * 时，前面都匹配到有效的字符

解题思路

1. 初始化：dp[0][0]是True，因为空字符串与空模式是匹配的。接下来初始化dp[0][j]，即当s为空字符串时p的匹配情况，只有当p的偶数位是*时可能为True。
2. 状态转移：考虑以下几种情况：
   • 当p[j-1]是普通字符时，只有当s[i-1]等于p[j-1]且dp[i-1][j-1]为True时，dp[i][j]才为True。
   • 当p[j-1]是.时，它可以匹配任意字符，只要dp[i-1][j-1]为True，dp[i][j]就为True。
   • 当p[j-1]是*时，需要考虑*匹配零个或多个字符的情况：
     • 匹配零个字符时，即*前面的字符被忽略，如果dp[i][j-2]是True，则dp[i][j]也是True。
     • 匹配一个或多个字符时，如果s[i-1]与*前面的字符匹配（或者*前面是.），并且dp[i-1][j]是True，则dp[i][j]也是True。
3. 返回结果：最后dp[len(s)][len(p)]就是整个问题的解。

完整代码

Java

public class Solution {
    public boolean isMatch(String s, String p) {
        boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
        dp[0][0] = true;

        for (int j = 2; j <= p.length(); j++) {
            dp[0][j] = p.charAt(j-1) == '*' && dp[0][j-2];
        }

        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= p.length(); j++) {
                if (p.charAt(j-1) == '.' || p.charAt(j-1) == s.charAt(i-1)) {
                    dp[i][j] = dp[i-1][j-1];
                } else if (p.charAt(j-1) == '*') {
                    dp[i][j] = dp[i][j-2] || (dp[i-1][j] && (p.charAt(j-2) == '.' || p.charAt(j-2) == s.charAt(i-1)));
                }
            }
        }

        return dp[s.length()][p.length()];
    }
}

Python

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        dp = [[False] * (len(p) + 1) for _ in range(len(s) + 1)]
        dp[0][0] = True

        for j in range(2, len(p) + 1):
            dp[0][j] = p[j-1] == '*' and dp[0][j-2]

        for i in range(1, len(s) + 1):
            for j in range(1, len(p) + 1):
                if p[j-1] in {s[i-1], '.'}:
                    dp[i][j] = dp[i-1][j-1]
                elif p[j-1] == '*':
                    dp[i][j] = dp[i][j-2] or dp[i-1][j] and p[j-2] in {s[i-1], '.'}

        return dp[len(s)][len(p)]

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

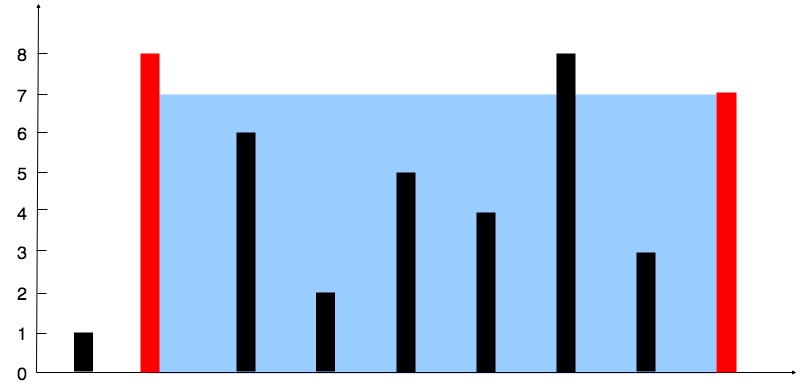
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

解题思路

1. 初始化：设置两个指针left和right，分别指向数组的开始和末尾。
2. 计算容量：计算由left和right指向的线段形成的容器可以存储的水量，容量计算公式为min(height[left], height[right]) * (right - left)。
3. 移动指针：比较left和right指向的高度，移动较短的一侧的指针，因为容器的容量是由较短的边界决定的，移动较长的边界不会增加容量。
4. 重复步骤2和3，直到left和right相遇。
5. 最大容量：在整个过程中，记录并更新可以得到的最大容量。

完整代码

Java

class Solution {
    public int maxArea(int[] height) {
        int left = 0, right = height.length - 1;
        int maxArea = 0;
        
        while (left < right) {
            int currentArea = Math.min(height[left], height[right]) * (right - left);
            maxArea = Math.max(maxArea, currentArea);
            
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }
        
        return maxArea;
    }

}

Python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        left, right = 0, len(height) - 1
        max_area = 0
        
        while left < right:
            # 计算当前容器的容量
            current_area = min(height[left], height[right]) * (right - left)
            max_area = max(max_area, current_area)
            
            # 移动较短的边界
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1
                
        return max_area