1.时间复杂度

衡量算法的好坏，使用大写的o来表示时间复杂度，通俗的讲，就是一个算法执行的次数；

时间复杂度就是数学里面的函数表达式；本质上是一个函数；

下面举几个例子：

(1)这里的执行次数是N*N+N，当有几项进行相加的时候，我们选择次数最高的，因为随着N的变大，次数低的项对表达式的影响越来越小，所以我们可以忽略，写作时间复杂度的形式就是o(N*N);

(2)如果是2个循环，一个执行M次，一个执行N次，他们的阶数相同，我们就写作o(M+N);

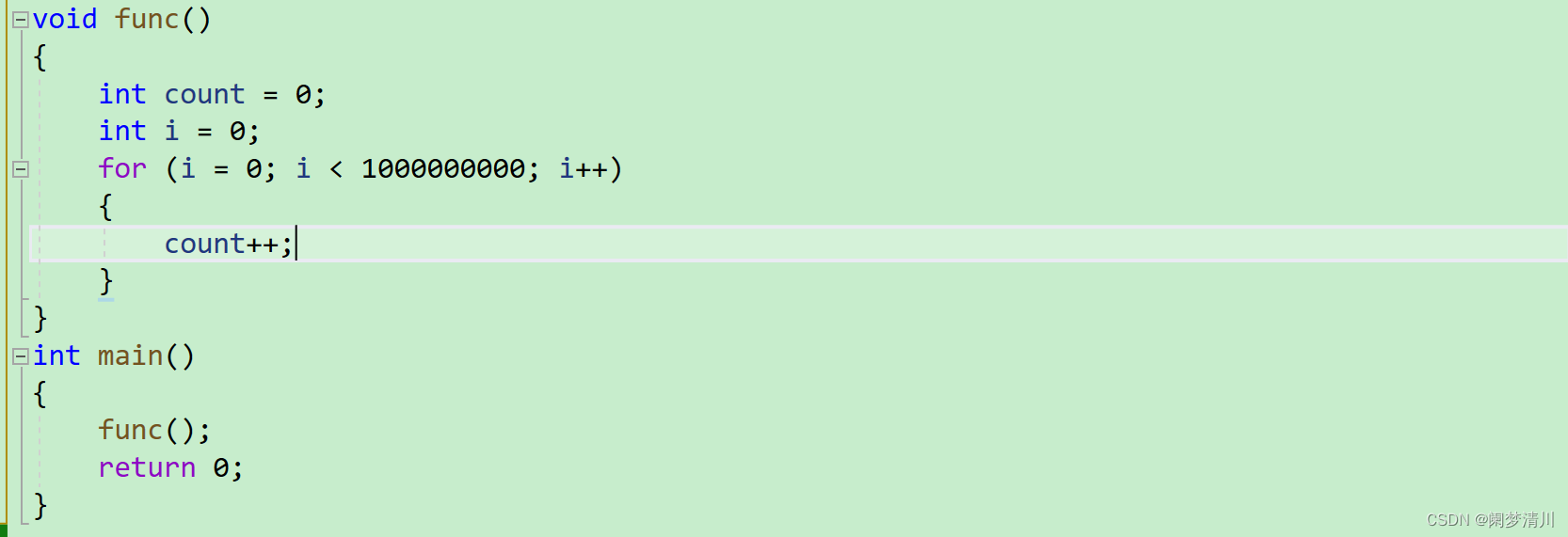
(3)这里是常数次，可以忽略不计，统一使用o(1)进行表示，这里的o(1)不是代表1次，而是代表常数次，就是确定的有限次，条件怎么变化，运算次数是确定的；

（4）

这里的时间复杂度是o(N),因为N无限大的时候，N和2N是没有区别的，while循环里面是有限次

所以跟N比起来就显得微不足道了，也可以忽略；

（5）如果是对于一个字符串，我们想要寻找某个字符，如何计算他的时间复杂度呢？如果我们的

运气比较好，可能在字符串的开头就找到了，稍微差点就会在中间找到，运气特别差的话可能需要

遍历整个字符串才能找到这个指定的字符，对于时间复杂度而言，我们会按照最坏的打算，这里是

降低预期，底线思维，时间复杂度记作O（N）；

（6）冒泡排序的时间复杂度：N个数字排序，实际上是等差数列的求和次数是N-1*N/2，高阶忽略系数就是N*N;

（7）二分查找的时间复杂度：二分查找找一次就缩小一般，找一次除以2，找一次除以2，2的x次方等于N，所以次数就是以2为底N的对数，写作O（log2N);

（8）

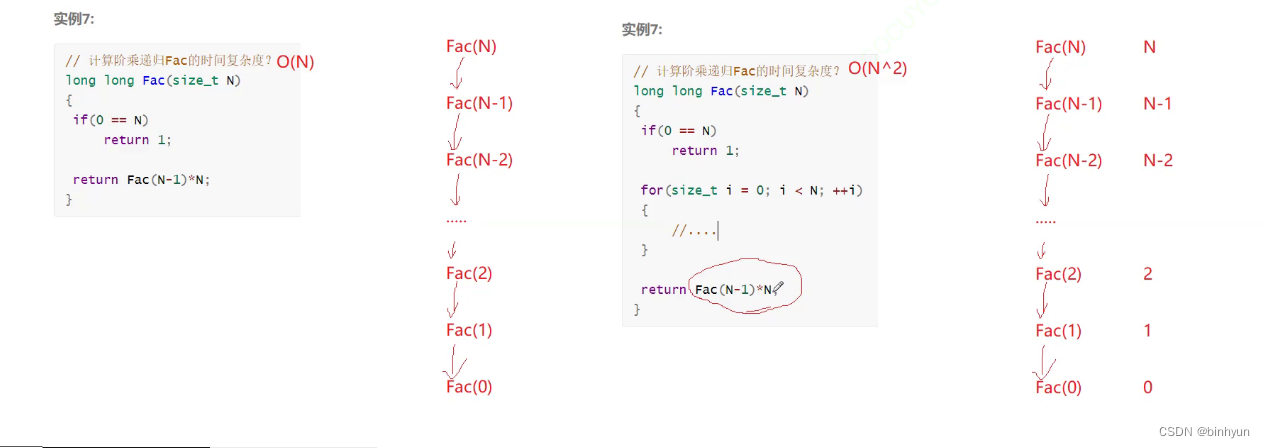
这个阶乘就比较难理解了，左边的调用N+1次，右边的每次都要经理N次循环，所以就是N*N；

2.时间复杂度的应用----消失的数字

（1）排序以后，判断下一个数字是不是上一个加上1，不是就找到了；

（2）使用0和所有的数字异或操作

比如这样的一串数据：013456789，先让0^每一个数字，进行遍历操作，^是符合交换律的，所以不需要担心他们出现的先后顺序，0^0=0-------0^1=1---------1^2=2--------以此推理，最后拿到的x就是9了，这里的size=9，循环从0开始，就是9次，我们使用i的话，需要和9^,这个时候的循环条件就是i<=size或者i<size+1;这里使用的是后者控制循环，相同的经过这两次循环里面的2次^就会变成0了，因为i是逐步递增的，所以数组里面少一个元素和i进行^得到0，这个数字在第二次的循环里面就被找到了。

(3)找到最小值，最大值，等差数列求和，减去所有的数值，就可以找到缺失的数字；

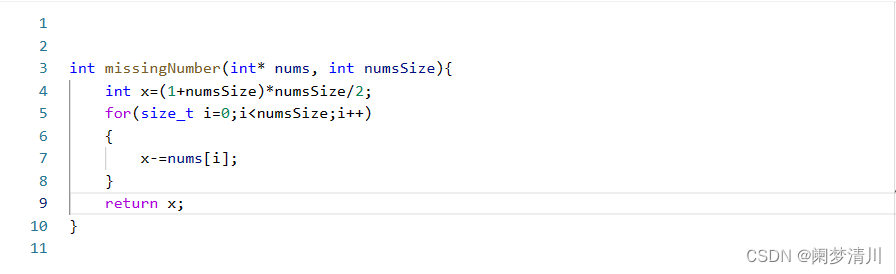
还是那013456789举例子吧，numsSize=10;我们进行求和的时候，首项0加上尾项numsSize,项数就是numsSize加上1了，x里面就是数列的和，利用循环减去每一个数字就找到了消失的数字。