前言
作者:小蜗牛向前冲
专栏:小蜗牛算法之路
专栏介绍:"蜗牛之道,攀登大厂高峰,让我们携手学习算法。在这个专栏中,将涵盖动态规划、贪心算法、回溯等高阶技巧,不定期为你奉上基础数据结构的精彩算法之旅。一同努力,追逐技术的星辰大海。"
目录
一、递归
1、什么是递归
2、为什么会用到递归
3、如何去理解递归
4、如何求写递归
二、搜索
1、深度和宽度
2、搜索
3、拓展搜索
三、回溯和剪枝
四、刷题时刻
1、汉诺塔问题
a、算法原理
b、代码实现
2、合并两个有序链表(easy)
a、算法原理
b、代码实现
3、反转链表(easy)
a、算法原理
b、代码实现
四、 两两交换链表中的节点(medium)
a、算法原理
b、代码实现
五、Pow(x, n)- 快速幂(medium)
a、算法原理
b、代码实现
这里是主讲算法刷题,一些概念可以看博主以前写的博客,下面会带链接。后面就不会在提醒了,大家开心刷题吧!
一、递归
1、什么是递归
简单的来说就是函数自调用自己。
在C语言的学习我们就接触了,然后在数据结构中的二叉数,快排,归并都有其身影。
不清楚看这里:
详解函数递归
[数据结构]~二叉树
[数据结构]-玩转八大排序(二)&&冒泡排序&&快速排序
[数据结构]-玩转八大排序(三)&&归并排序&&非比较排序
2、为什么会用到递归
本质是为由主问题拆分到子问题,再由相似的子问题拆分到相同的子问题。
如二叉树的遍历

快排
归并排序

3、如何去理解递归
初学可以画递归展开图
在求做二叉树的简单题目
最后宏观的看到递归过程:
- 不在拘泥于递归展开图
- 把递归想象为一个黑盒
- 让黑盒求完成任务
4、如何求写递归
- 先找到相同的子问题---->想函数的头。
- 只关心子问题是如何解决的---->写出函数主体
- 注意递归函数的出口
二、搜索
1、深度和宽度
深度优先遍历vs 深度优先搜索(dfs)
深度优先遍历
其中深度优先表示从根节点开始,沿着每个分支尽可能深入,直到达到树或图的最底部,然后回溯到上一层,继续遍历其他分支。在这个过程中,我们尽可能深入地探索一个分支,直到无法继续为止,然后回溯。
深度优先搜索(Depth-First Search,DFS):
用于描述在图或树等数据结构上进行搜索的算法。DFS 是一种算法,通过深度优先的方式遍历或搜索图或树。它通常与递归或使用栈的迭代方法结合使用。DFS 通常用于解决图的连通性问题、拓扑排序、路径查找等问题。
这二个概念其实在某种程度是是一样的:我们只要记住他就是一条路走到黑。
宽度优先遍历vs 宽度优先搜索(bfs)
宽度优先遍历(Breadth-First Traversal):
宽度优先遍历从根节点开始,逐层地访问节点,先访问距离根节点最近的节点,然后是相邻的、同一层级的节点,依此类推,直到遍历完整个数据结构。
宽度优先搜索(Breadth-First Search,BFS):
它从根节点开始,逐层地探索图中的节点,先探索距离起始节点最近的节点,然后是相邻的、同一层级的节点,依此类推,直到找到目标节点或者遍历完整个数据结构。
这二个概念其实在某种程度是是一样的:我们只要记住他就一层层走的。
2、搜索
简单的来说就是暴力枚举一遍所以数据。
通过dfs或者bfs .
3、拓展搜索
其实搜索不仅仅局限鱼树或图等数据结构问题求解,只要一个问题的子问题可以全排列为,一课树状图的问题都可以用搜索解决。
比如对于1,2,3进行全排列
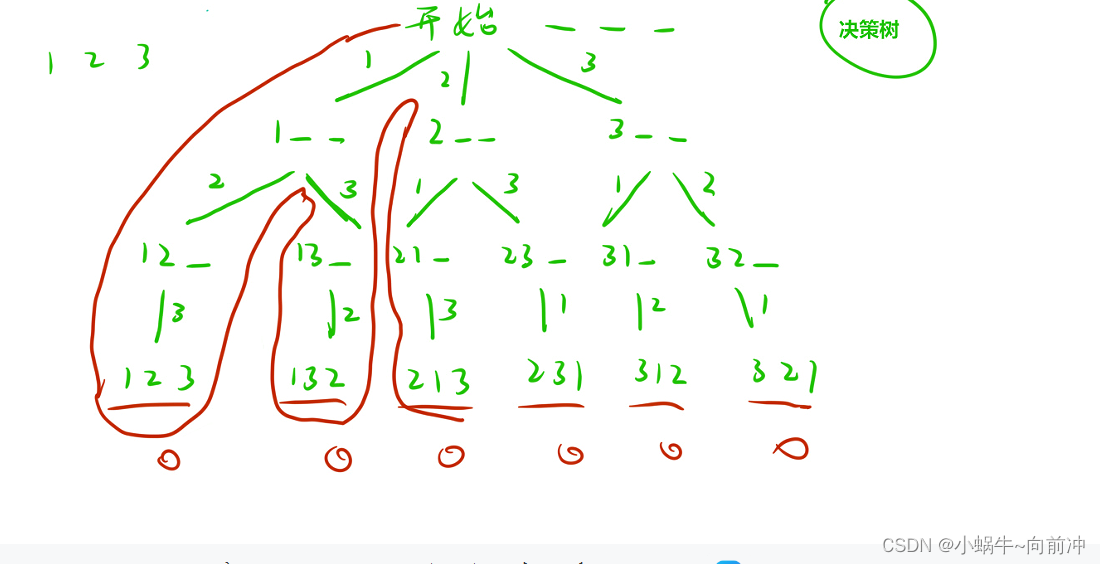
三、回溯和剪枝
回溯本质就是深搜,剪枝的本质就是将回溯过后发现不对的部分去掉。
拿下面的走迷宫举例:
=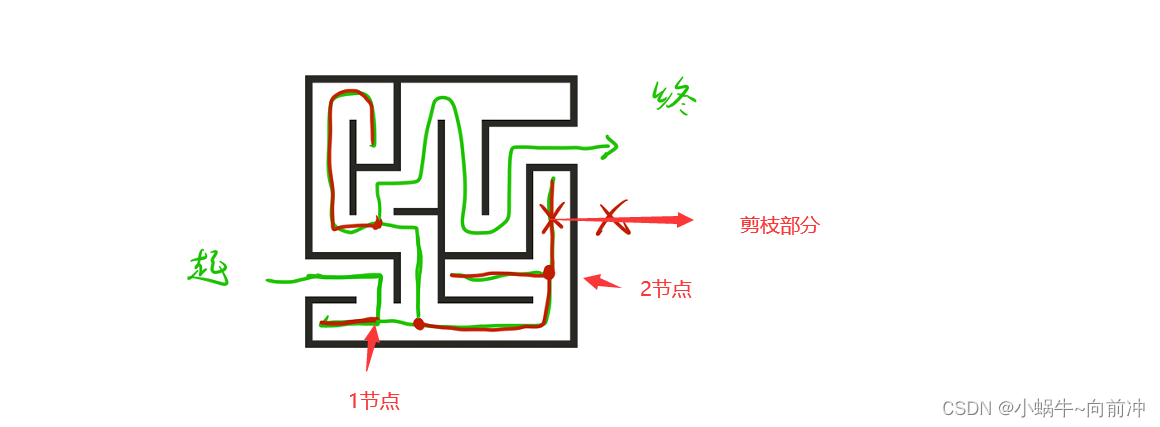
首先我们从起点出发通过深度搜索来都到1节点,有二条路,走向红色那一条,碰壁后返回的1节点的过程就是回溯。在来看2节点, 发现二路都不对,回溯后将那二条路去掉的过程就是剪枝。
四、刷题时刻
1、汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
示例1:
输入:A = [2, 1, 0], B = [], C = [] 输出:C = [2, 1, 0]示例2:
输入:A = [1, 0], B = [], C = [] 输出:C = [1, 0]提示:
- A中盘子的数目不大于14个。
class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
}
};a、算法原理
拿到一个题目,我们完成对题意的理解后,首先会想:
怎么去解决这个问题?

一般情况:我们都是按照题意先试试着去模拟。
当N==1时:我们直接把一个盘子从A移动C
当N==2时:我们要想把大盘上面的小盘,放在B,在把大盘放在C后,将小盘移动过来C。
当N==3时:我们把大盘上面的部分想办法移动到B,然后在把大便移动到C,最后想办法将小盘部分移动到C就可以了、
当N==n,时候,重复上图序号的过程就可以了
这种情况不就,我们将一个大问题,转换为一个子问题,子问题在转换为,同类型的子问题。所以这就切合递归。
递归解题思路:
1、重复问题---函数头
重复问题:将x柱子上面的盘子,借助y柱子,移动到z柱子上
函数头: void dfs(x,y,z,n)
2、只关系子问题在做什么
这里以N==3来切入思考:
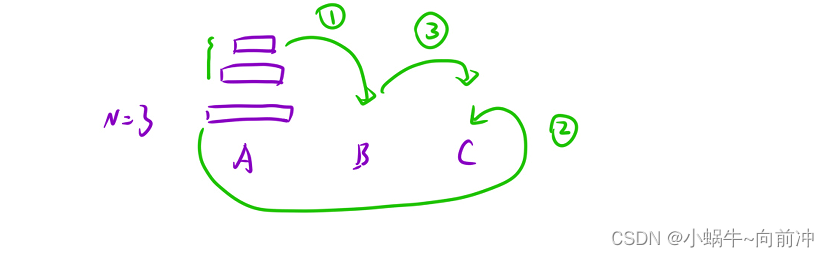
dfs(x,z,y,n-1) --- B 将大盘上面的盘子移走(1)
x.back() ---C 将大盘子移动到z柱子上(2)
dfs(y ,x,z)--->C 将小盘部分移动到z柱子上(3)
这里自己可以简单画图理解!
3、递归的出口在哪里
N==1的时候,我们就不要在借助其他盘子了,直接移动到z柱子上就可以了。
x.back() ---z;
b、代码实现
class Solution {
public:
void hanota(vector<int>& A, vector<int>& B, vector<int>& C)
{
int n = A.size();
dfs(A, B, C, n);
}
void dfs(vector<int>& x, vector<int>& y, vector<int>& z, int n)
{
//递归出口
if (n == 1)
{
z.push_back(x.back());
x.pop_back();
return;
}
//函数体
dfs(x, z, y, n - 1);
z.push_back(x.back());
x.pop_back();
dfs(y, x, z, n - 1);
}
};LeetCode测试:

2、合并两个有序链表(easy)
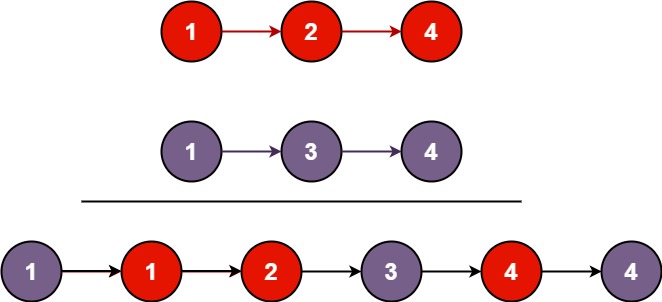
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4] 输出:[1,1,2,3,4,4]示例 2:
输入:l1 = [], l2 = [] 输出:[]示例 3:
输入:l1 = [], l2 = [0] 输出:[0]提示:
- 两个链表的节点数目范围是
[0, 50]-100 <= Node.val <= 100l1和l2均按 非递减顺序 排列1
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
}
};a、算法原理
合并二个升序的链表,我们只要先从二个链表头结点选出,最小的那个结点拿出来,其余形成二个新的链表,我们让函数dfs帮我们合成一个链表,在链接最小的那个结点。这不就相同的子问题吗?

所以我们这里可以用递归解决:
函数头:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
函数体:相同的子问题:
从二个链表头结点选出最小的那个list1(假设为最小)
list1->next = mergeTwoLists(list1->next, list2) ;
return list1;
递归结束:
那个链表为空就返回另外一个链表。
b、代码实现
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2)
{
if (list1 == nullptr)
return list2;
if (list2 == nullptr)
return list1;
if (list1->val < list2->val)
{
list1->next = mergeTwoLists(list1->next, list2);
return list1;
}
else
{
list2->next = mergeTwoLists(list1, list2->next);
return list2;
}
}
};LeetCode测试:

3、反转链表(easy)
给你单链表的头节点
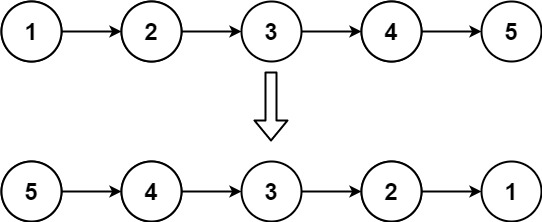
head,请你反转链表,并返回反转后的链表。示例 1:
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2:
输入:head = [1,2] 输出:[2,1]示例 3:
输入:head = [] 输出:[]提示:
- 链表中节点的数目范围是
[0, 5000]-5000 <= Node.val <= 5000进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
}
};a、算法原理
既然这道题目可以用递归解决问题,那么翻转整体链表,就可以分为一个子问题。
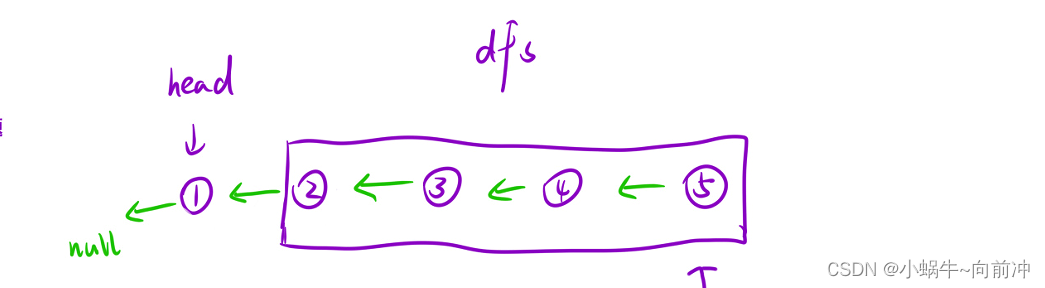
视角一:从宏观视角看
我们要翻转链表,可以分为:
- 让当前结点后面的结点链表进行逆置,返回头结点就好了
- 让当前结点添加到后面逆置链表即可
视角二:将链表看成一颗树
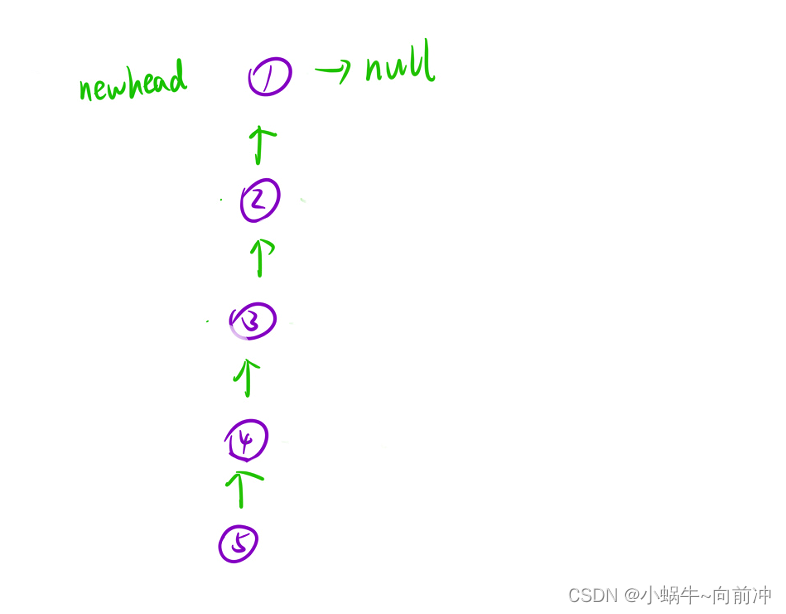
那不就只进行一次dfs遍历就好了(树的后序遍历)
递归实现:
函数头
ListNode* reverseList(ListNode* head)
子问题
ListNode* newhead = reverseList(head->next);
//将当前结点连接到逆置链表
head->next->next = head;
head->next = nullptr;
递归的出口在哪里
当head==nullptr 或者head->next==nullptr;
return head;
b、代码实现
class Solution {
public:
ListNode* reverseList(ListNode* head)
{
//一个结点或者没有结点就不需要逆置
//细节不要这样会报错if(head->next==nullptr||head==nullptr)
//表达式是有顺序的这样会先判断:head->next==nullptr
//但是要是head为nullptr就是空指针的引用了
if (head == nullptr || head->next == nullptr)
return head;
//子问题
//返回逆置当前结点后面链表,返回新头结点
ListNode* newhead = reverseList(head->next);
//将当前结点连接到逆置链表
head->next->next = head;
head->next = nullptr;
//返回新的头结点
return newhead;
}
};LeetCode测试:

四、 两两交换链表中的节点(medium)
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
示例 1:
输入:head = [1,2,3,4] 输出:[2,1,4,3]示例 2:
输入:head = [] 输出:[]示例 3:
输入:head = [1] 输出:[1]提示:
- 链表中节点的数目在范围
[0, 100]内0 <= Node.val <= 100
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
}
};a、算法原理
对于链表类问题,大家一定要画图前理解。

首先站宏观的视角看待,我们要将相邻二个结点交换,我们可以分为前二个结点,和后面一段,后面一段我们交给一个函数swapPairs我相信他一定能完成对里面结点进行交换,怎么完成的我们不关心。
然后在如图进行连接。
那递归结束的条件是什么:
当我们的结点为空或者只有一个节点就返回head.
b、代码实现
class Solution {
public:
ListNode* swapPairs(ListNode* head)
{
if (head == nullptr || head->next == nullptr)
return head;
ListNode* tmp = swapPairs(head->next->next);
ListNode* newhead = head->next;
newhead->next = head;
head->next = tmp;
return newhead;
}
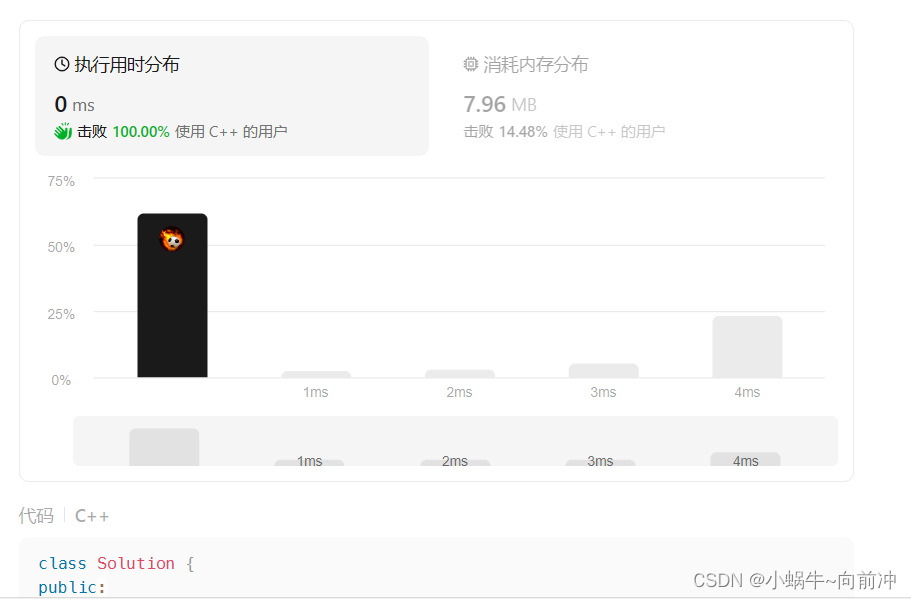
};LeetCode测试:

五、Pow(x, n)- 快速幂(medium)
实现 pow(x, n) ,即计算
x的整数n次幂函数(即,xn)。示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000示例 2:
输入:x = 2.10000, n = 3 输出:9.26100示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
class Solution {
public:
double myPow(double x, int n) {
}
};a、算法原理
这道题目最容易想到是暴力,就是遍历相乘就好了,但是这样肯定是会超时的。
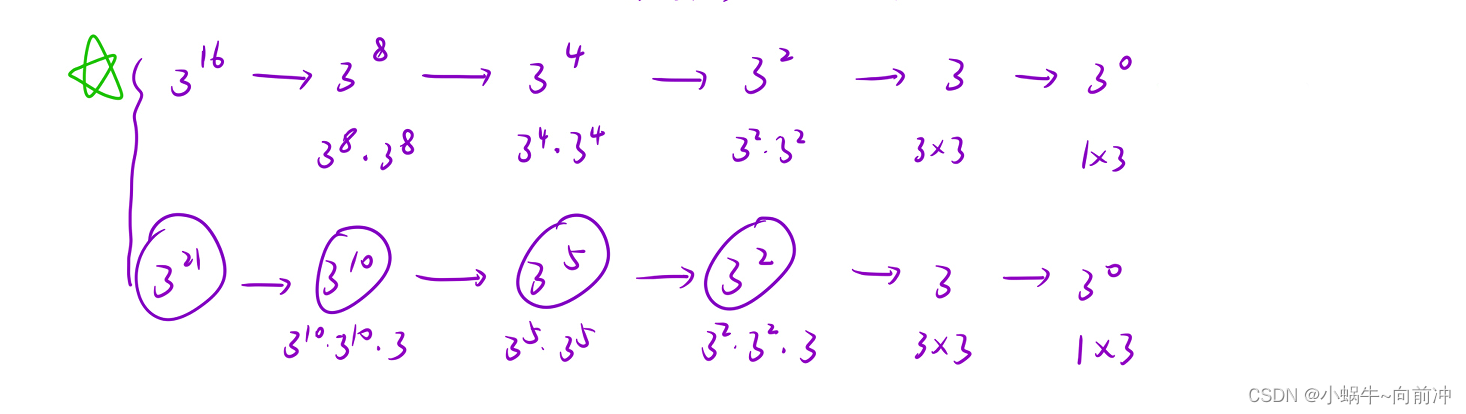
我们可以思考一下:当我们 x和n为上面二种情况的时候,我们通过不断划分子问题,从而求出结果,这不就是递归吗?
函数头:int pow(x,n)我们相信这函数可以帮助我们进行幂计算
函数体:只关系子问题做了什么
tmp = pow(x,n/2);
return n%2==0? tmp*tmp:tmp*tmp*x
递归出口:n==0时return 1;
细节问题:
n可能出现负数:
也就是说可能出现3^(-2) 那我们的计算结果应该是1/(3^(2))
n可能为
:
如果我们把他转换为正数处理,int是存放不下的,所以我们要用long long去存(进行强转)
b、代码实现
class Solution {
public:
double myPow(double x, int n)
{
return n > 0 ? Pow(x, n) : 1.0 / Pow(x, -(long long)n);
}
double Pow(double x, long long n)
{
if (n == 0)
return 1.0;
double tmp = Pow(x, n / 2);
return n % 2 == 0 ? tmp * tmp : tmp * tmp * x;
}
};












![[C语言]——分支和循环(4)](https://img-blog.csdnimg.cn/direct/d0a718175c6245c2a7094d5c2b9fbc19.png)