目录
- 1. 双指针
- 1.1 移动 "0"
- 1.2 复写 "0"
- 1.3 快乐数(快慢指针)
- 1.4 盛水最多的容器(单调性原则)
- 1.5 有效三角形个数
- 1.6 两个数之和
- 1.7 三数之和
- 1.8 四数之和
1. 双指针
1.1 移动 “0”
- 题目信息:
- 题目链接:
移动 “0”
思路演示:
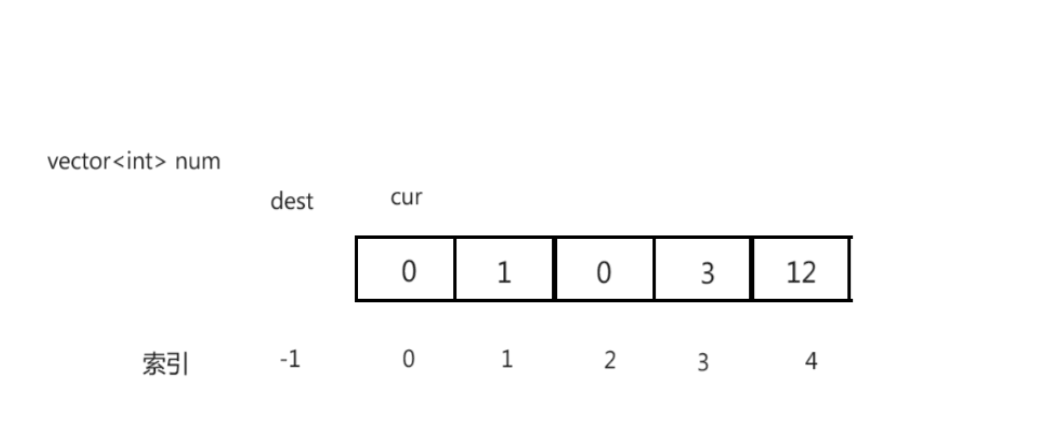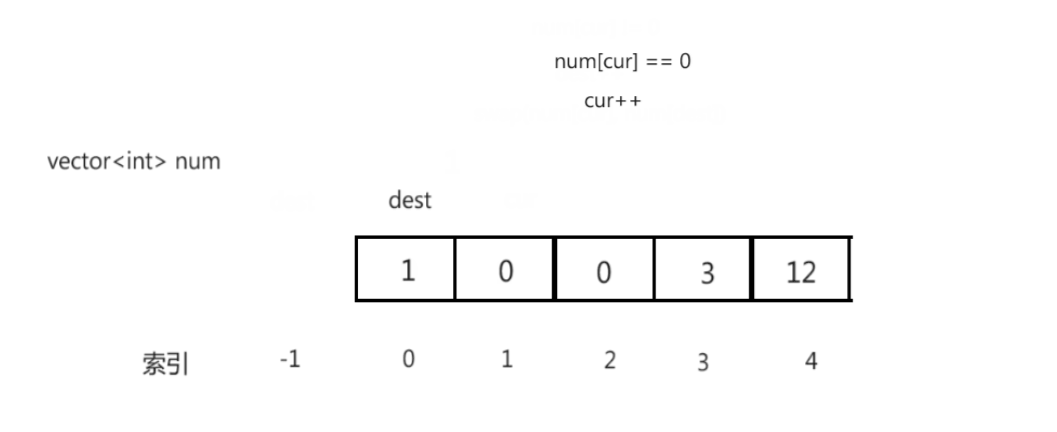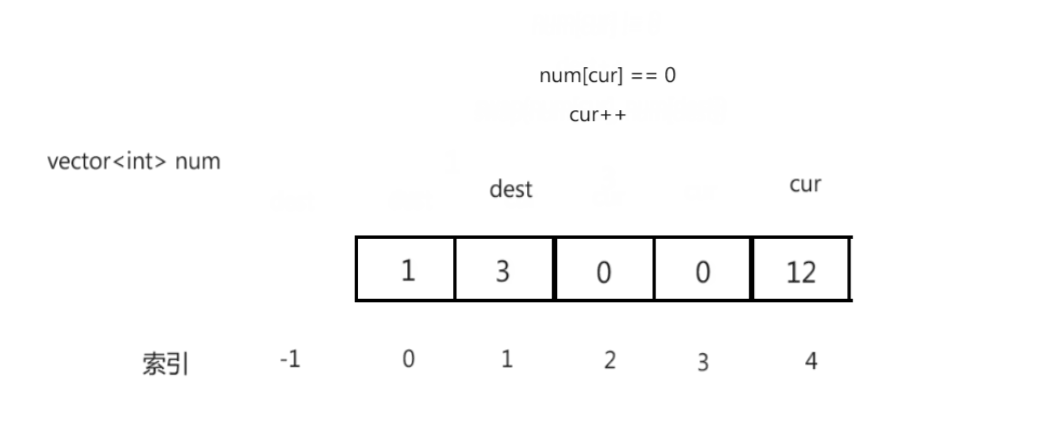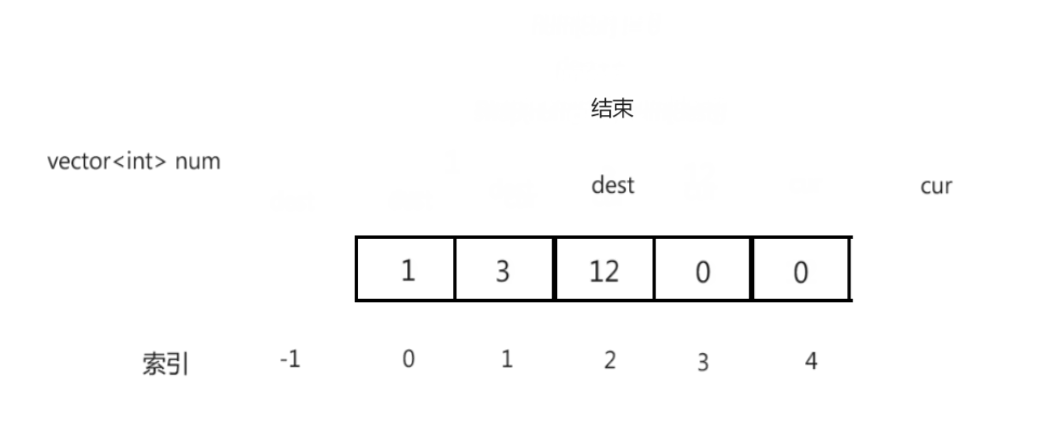
补充:
- [0, dest]区间内的元素都为0
- [dest + 1, cur]区间内的元素都不为0
- cur指针遍历完数据,调整结束
class Solution
{
public:
void moveZeroes(vector<int>& nums)
{
int dest = -1;
int cur = 0;
while(cur < nums.size())
{
if(nums[cur])
{
swap(nums[cur], nums[++dest]);
}
cur++;
}
}
};
1.2 复写 “0”
- 题目信息:
- 题目链接:
复写"0"
思路演示:
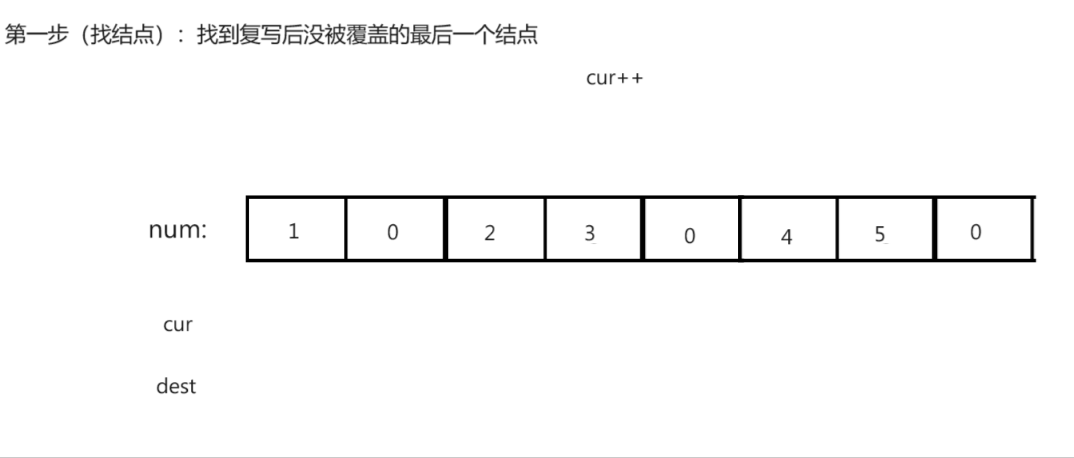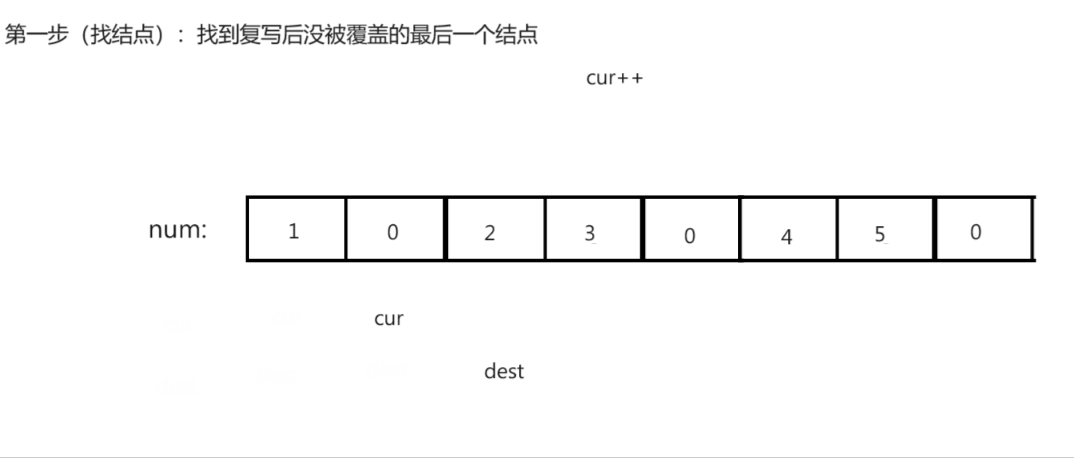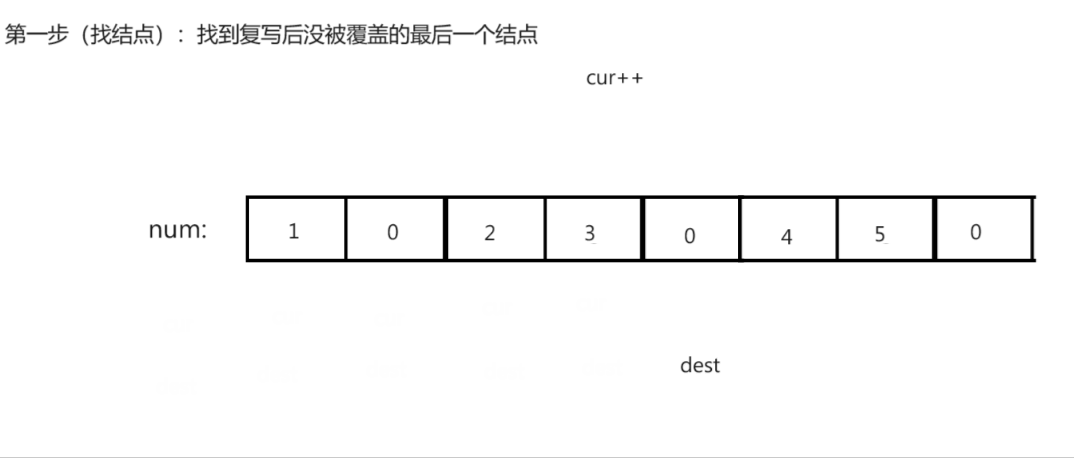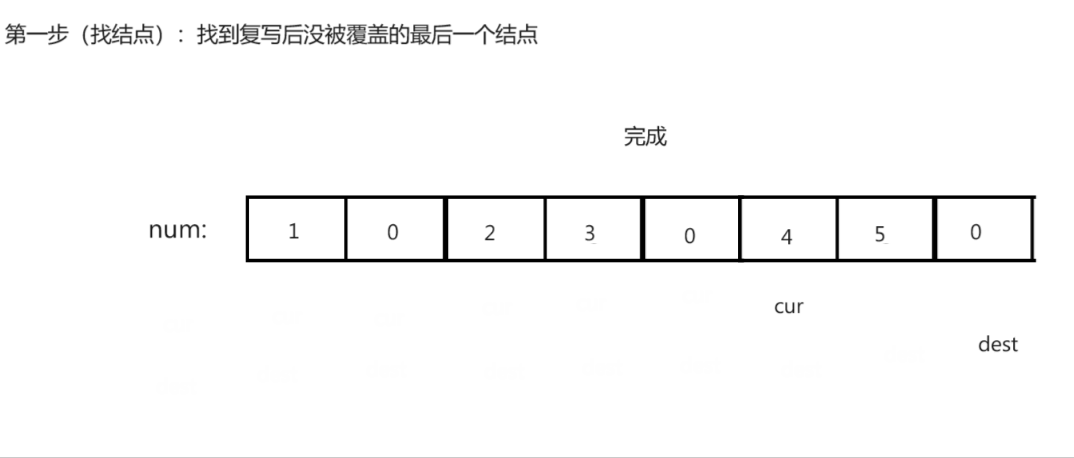
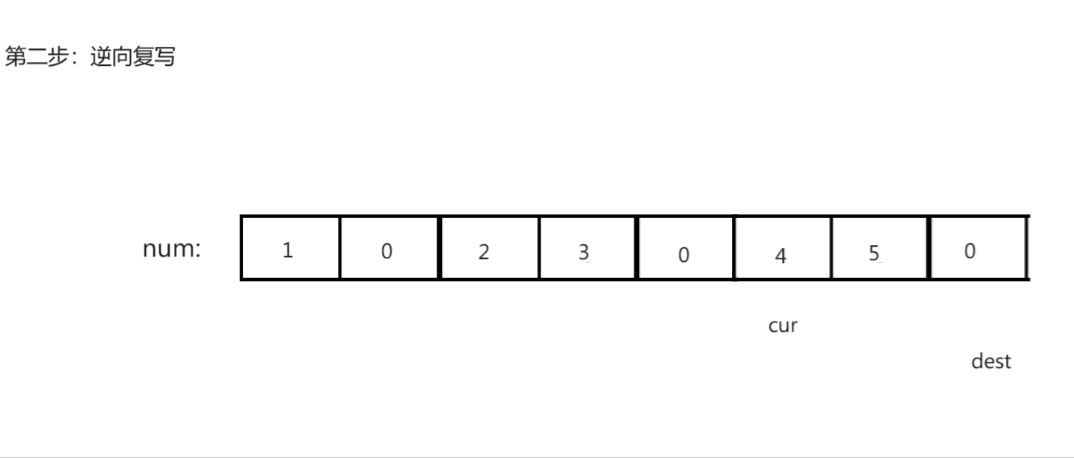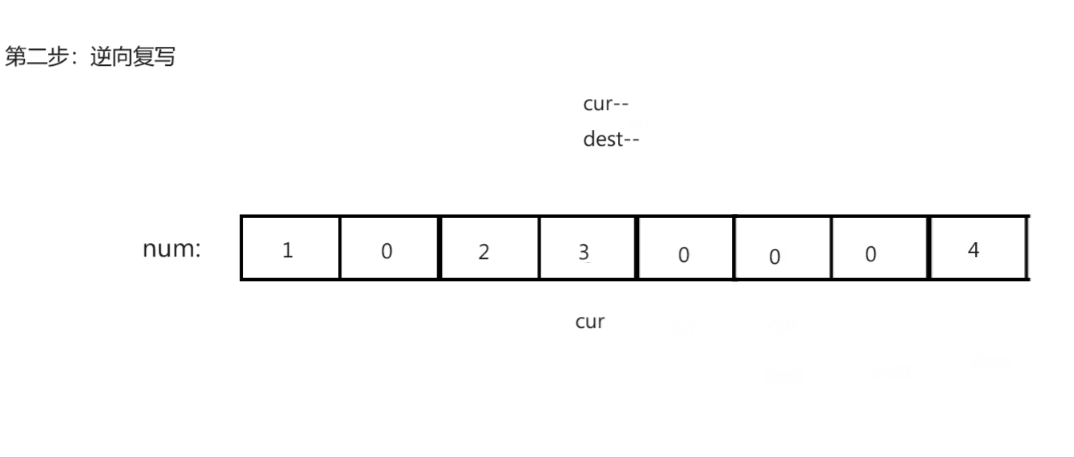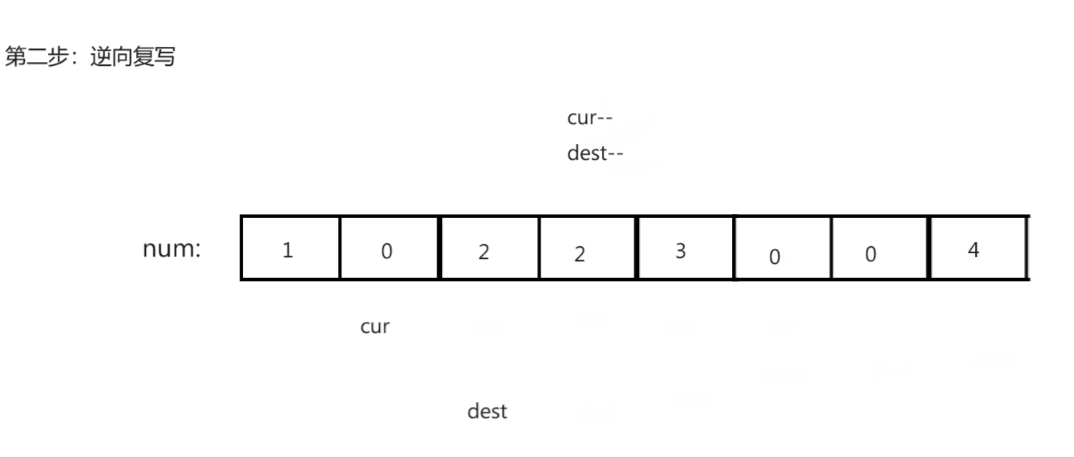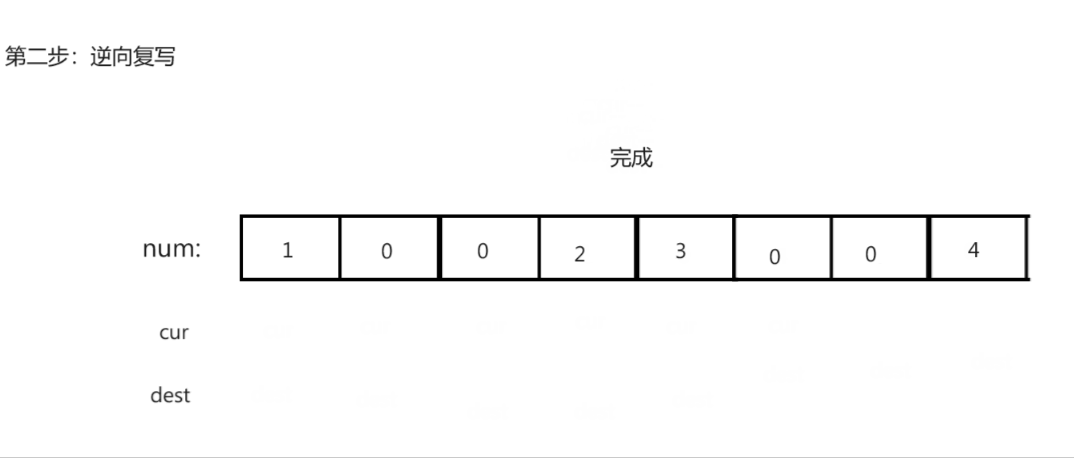
注意:
- 寻找最后未覆盖结点时可能回导致dest越界,从而导致逆向复写的过程中出现越界错误。
例:[0, 0, 0]
因此,需要对此种越界情况做特殊处理。
class Solution
{
public:
void duplicateZeros(vector<int>& arr)
{
//找结点
int cur = -1;
int dest = -1;
int size = arr.size();
while (dest < size - 1)
{
cur++;
if (arr[cur] == 0)
{
dest += 2;
}
else
{
dest++;
}
}
//越界可能
while(cur >= 0)
{
if(arr[cur] == 0)
{
//特殊处理
if(dest > size - 1)
{
arr[--dest] = arr[cur];
}
else
{
arr[dest] = arr[cur];
arr[--dest] = arr[cur];
}
}
else
{
//特殊处理
if(dest > size - 1)
{
arr[--dest] = arr[cur];
}
else
{
arr[dest] = arr[cur];
}
}
dest--;
cur--;
}
}
};
1.3 快乐数(快慢指针)
- 题目信息:
- 题目链接:
快乐数
过程演示:
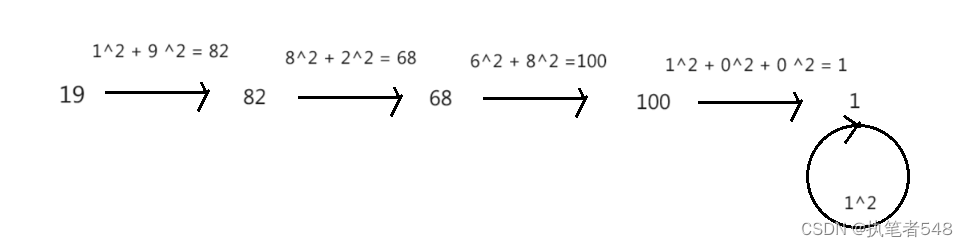
注: 无论数n是否为快乐数,其进行快乐数的判断逻辑一定都会进入一个循环。我们将每次运算得出的结果视为结点,平方和的运算步骤视为链表的一步。那么,上述问题就可以理解为链表循环问题。(是否为只有1的环)
class Solution
{
public:
int gethappy(int num)
{
int sum = 0;
while(num)
{
sum += (num % 10) * (num % 10);
num /= 10;
}
return sum;
}
bool isHappy(int n)
{
//环状链表,快慢指针
int quick = n;
int slow = n;
do
{
//快慢指针
//走一步
slow = gethappy(slow);
//走两步
quick = gethappy(quick);
quick = gethappy(quick);
}while(slow != quick);
if(slow == 1)
{
return true;
}
return false;
}
};
1.4 盛水最多的容器(单调性原则)
- 题目信息:
- 题目链接:
盛水最多的容器
过程演示:
思路1:求出所有的容积,然后在其中选出最大(暴力求解)
思路2:单调性原则
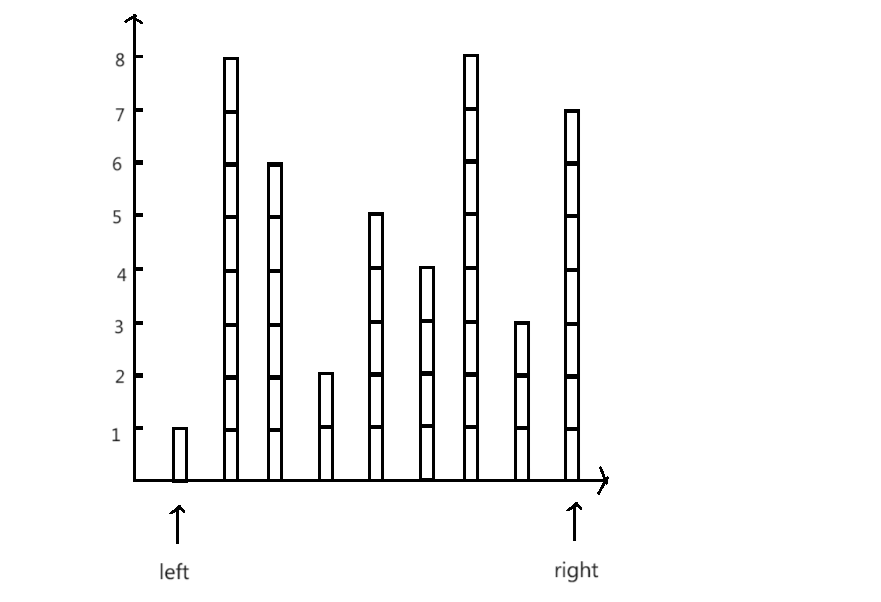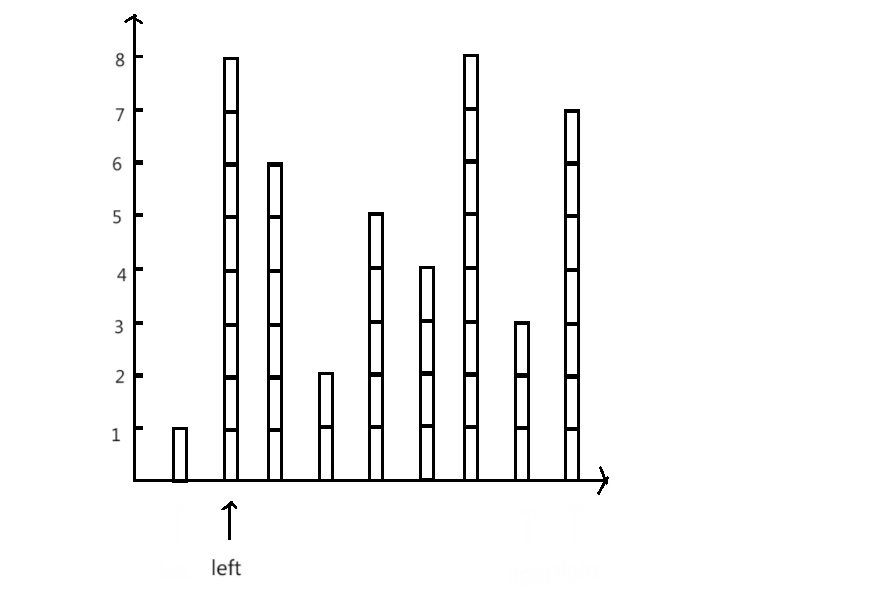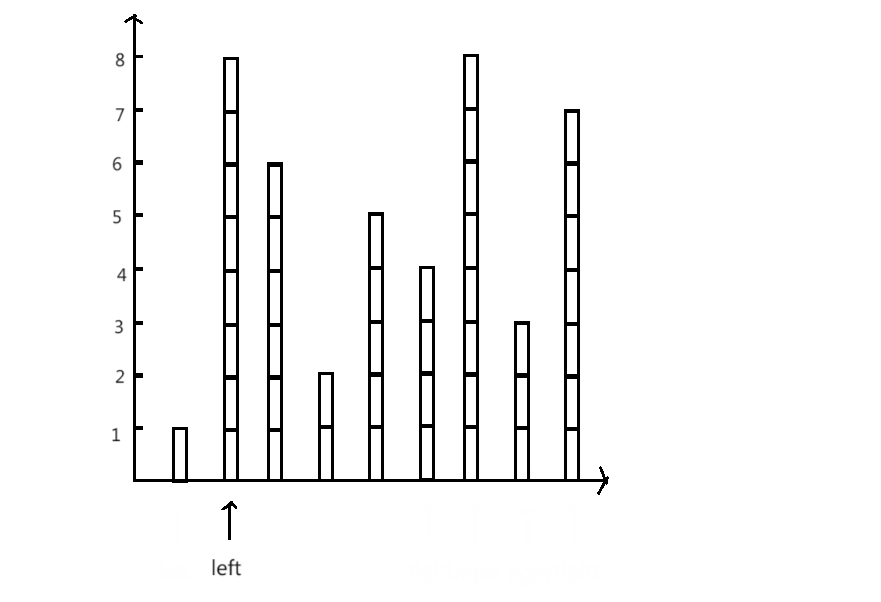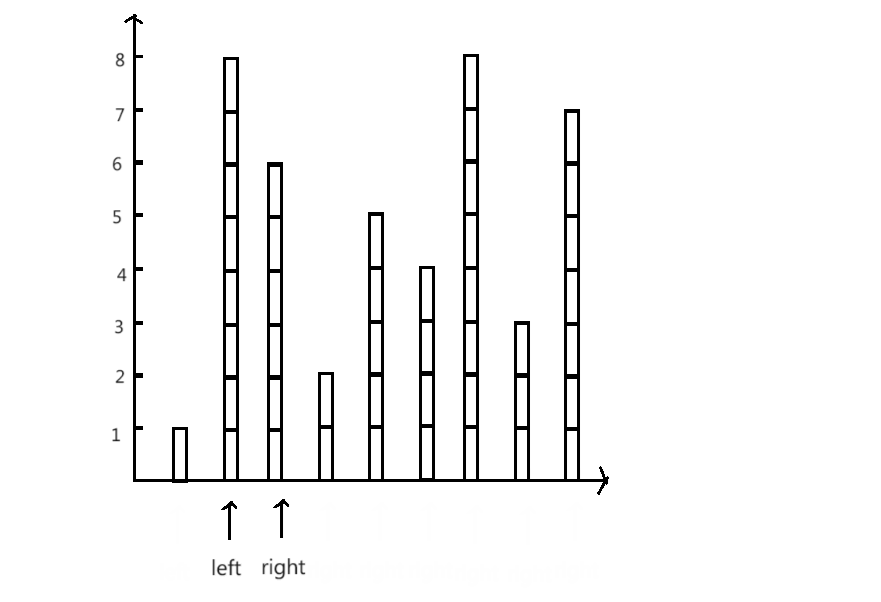
- 容器的的高是由短边决定的
- 因此可以确定在高不变的情况下,移动长边只会导致底变短
- 所以可以确定当前的搭配是以短边为高一组中,容积最大的
只需记录每组中最大的容积,算法时间复杂度优化为O(n)
class Solution {
public:
int maxArea(vector<int>& height)
{
//单调性原则
//将小边丢掉
int left = 0;
int right = height.size() - 1;
vector<int> area;
while(left < right)
{
if(height[left] < height[right])
{
area.push_back((right - left) * height[left]);
left++;
}
else
{
area.push_back((right - left) * height[right]);
right--;
}
}
int max = area[0];
for(auto e : area)
{
if(e > max)
{
max = e;
}
}
return max;
}
};
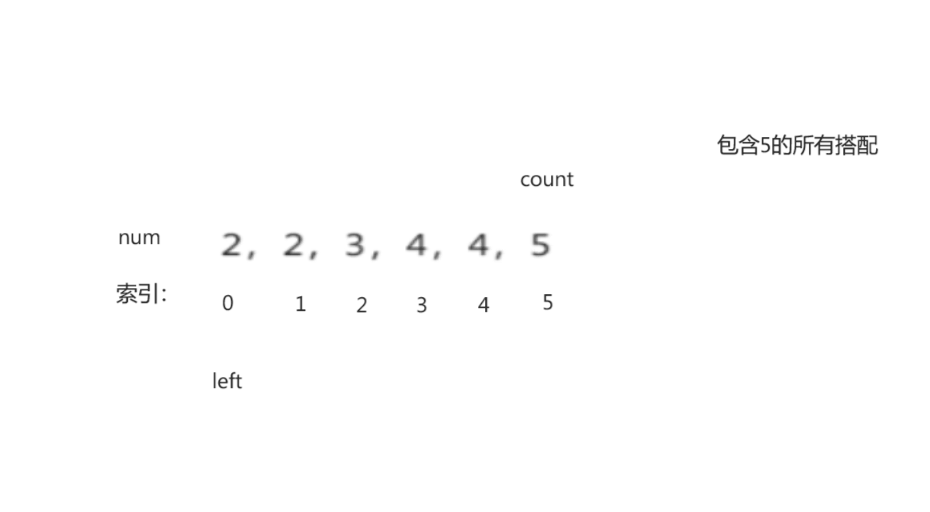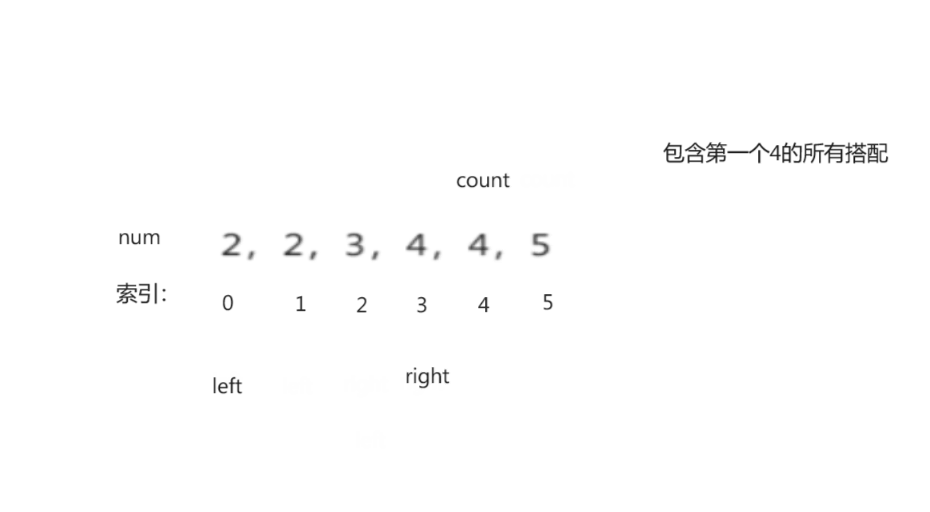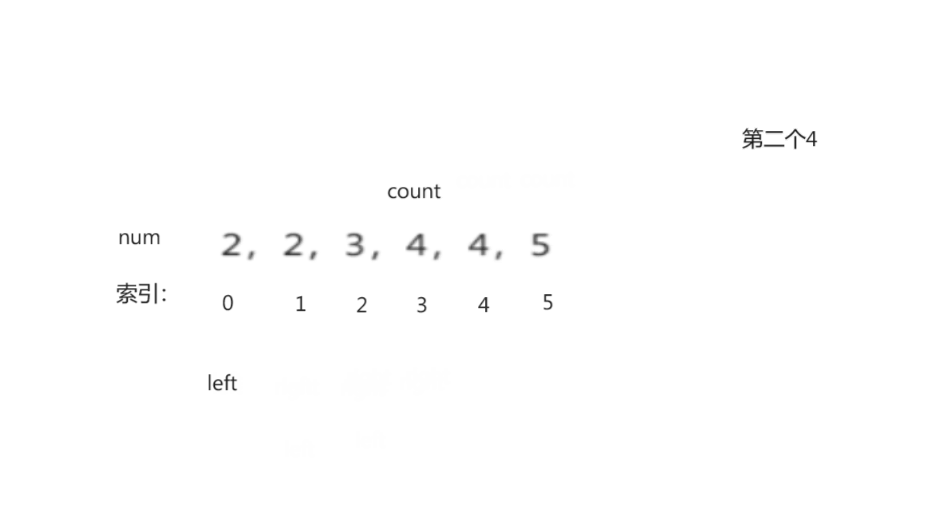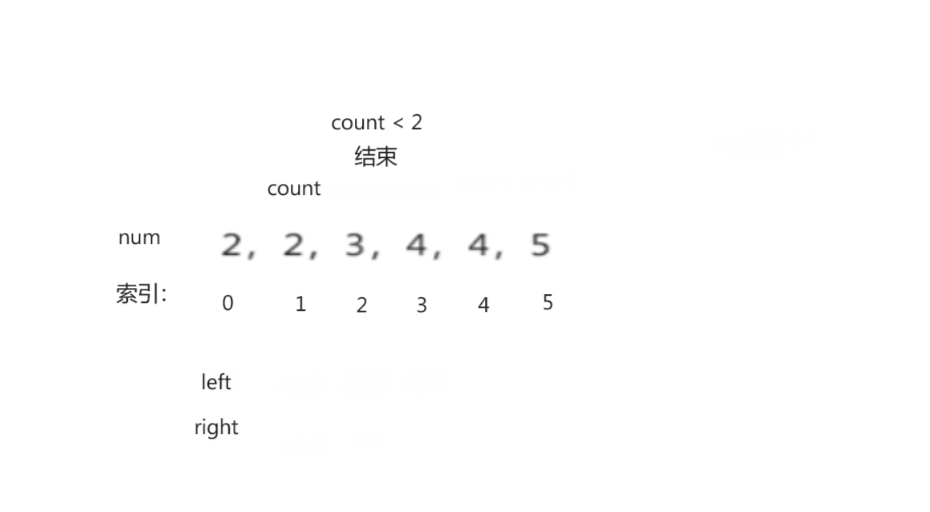
1.5 有效三角形个数
- 题目信息:
- 题目链接:
有效三角形个数- 思路:
<1> 先将所给数组进行排序(升序)
<2> 判断三个数是否能够组成三角形的三个边:任意两边之和大于第三边
<3> 指针对撞法(优化暴力求解)
过程演示:
class Solution
{
public:
int triangleNumber(vector<int>& nums)
{
//任意两边之和大于第三边
//优化先排序再判断
sort(nums.begin(), nums.end());
int times = 0;
int count = nums.size() - 1;
int left = 0;
int right = count - 1;
while(count >= 2)
{
while(right >= 1)
{
while(left < right && nums[right] + nums[left] <= nums[count])
{
left++;
}
if(left < right)
{
times += (right - left);
}
right--;
}
left = 0;
count--;
right = count - 1;
}
return times;
}
};
1.6 两个数之和
- 题目信息:
- 题目链接:
两数之和- 思路:
<1> 若两数之和大于等于指定数,移动右指针
<2> 若两数之和小于指定数,移动左指针
直至两指针相撞
过程演示:

class Solution
{
public:
vector<int> twoSum(vector<int>& price, int target)
{
vector<int> goods;
//大挪右,小挪左
int left = 0;
int right =price.size() - 1;
while(left < right && price[left] + price[right] != target)
{
if(price[left] + price[right] > target)
{
right--;
}
if(price[left] + price[right] < target)
{
left++;
}
}
if(left < right)
{
goods.push_back(price[left]);
goods.push_back(price[right]);
}
return goods;
}
};
1.7 三数之和
- 题目信息:
- 题目链接:
三数之和- 思路:
<1> 将整个数组排序,固定一个数num,创建两个指针left(最左则)与right(固定数num的前一个元素)
<2> 左右指针开始遍历数组,arr[left] + arr[right] < num,left指针右移,arr[left] + arr[right] > num,right指针左移,当arr[left] + arr[right] > num时,记录此次搭配。重复遍历步骤,直至left >= right,结束此次遍历
<3> 重复步骤2,直至num < 2
过程演示:
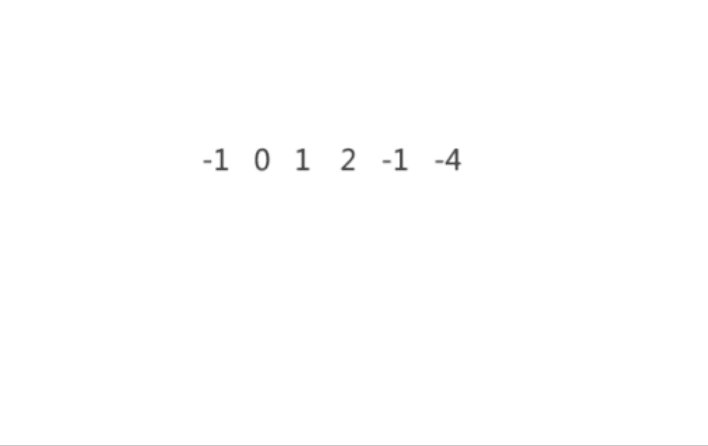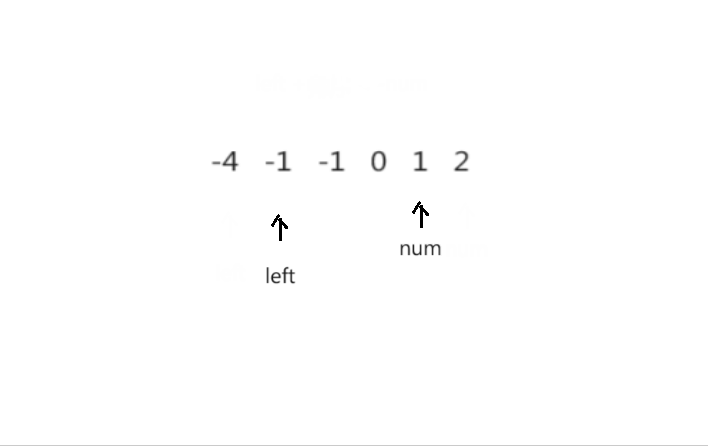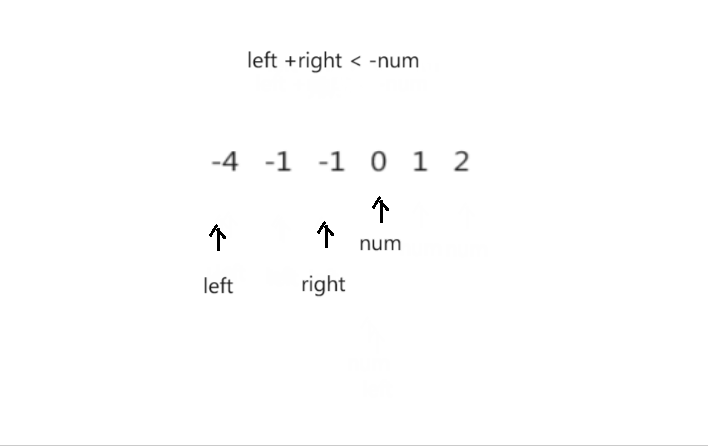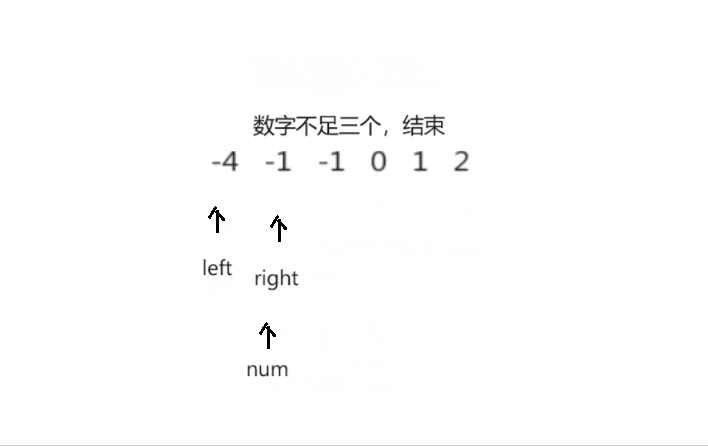
class Solution
{
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
//排序
//去重
//单调性
vector<vector<int>> v1;
sort(nums.begin(), nums.begin() + nums.size());
int cur = nums.size() - 1;
int right = 0;
int left = 0;
while (cur > 1)
{
right = cur - 1;
left = 0;
//一次遍历
while (right > left)
{
//判断同时去重
if ((right < cur - 1 && nums[right] == nums[right + 1]) || nums[right] + nums[left] > -nums[cur])
{
right--;
}
else if ((left > 0 && nums[left] == nums[left - 1]) || nums[right] + nums[left] < -nums[cur])
{
left++;
}
else
{
//记录
vector<int> v2;
v2.push_back(nums[left]);
v2.push_back(nums[right]);
v2.push_back(nums[cur]);
v1.push_back(v2);
right--;
}
}
//去重
do
{
cur--;
} while (cur > 1 && nums[cur] == nums[cur + 1]);
}
return v1;
}
};
1.8 四数之和
- 题目信息:
- 题目链接:
四数之和- 思路:在三指针的基础上再套一层
- 注:int类型存在数据溢出的风险
class Solution
{
public:
vector<vector<int>> fourSum(vector<int>& nums, int target)
{
sort(nums.begin(), nums.end());
vector<vector<int>> vv;
int end = nums.size() - 1;
int a = 0;
while (end - a + 1 >= 4)
{
int b = a + 1;
while (end - b + 1 >= 3)
{
int left = b + 1;
int right = end;
while (left < right)
{
int sum = nums[left] + nums[right];
long long goal = (long long)target - nums[a] - nums[b];
//去重
if ((right < end && nums[right + 1] == nums[right]) || sum > goal)
{
right--;
}
else if ((left > b + 1 && nums[left - 1] == nums[left]) || sum < goal)
{
left++;
}
else
{
vector<int> v;
v.push_back(nums[a]);
v.push_back(nums[b]);
v.push_back(nums[left]);
v.push_back(nums[right]);
vv.push_back(v);
left++;
}
}
do
{
b++;
} while (end - b + 1 >= 3 && nums[b - 1] == nums[b]);
}
do
{
a++;
} while (end - a + 1 >= 4 && nums[a - 1] == nums[a]);
}
return vv;
}
};