代码随想录第52天| ● 392.判断子序列 ● 115.不同的子序列

news2024/11/19 6:36:51

文章目录

● 392.判断子序列
- 思路
- 代码：
● 115.不同的子序列
- 思路：
- 代码：

● 392.判断子序列

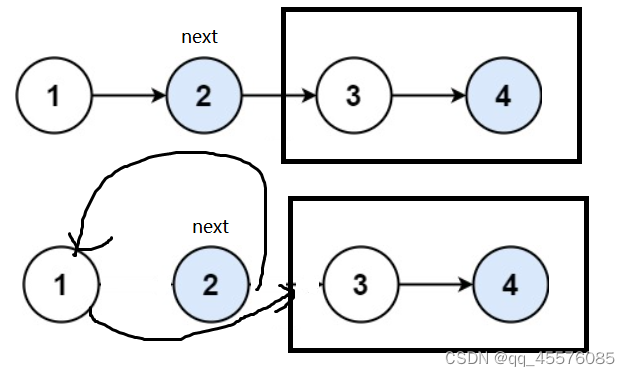
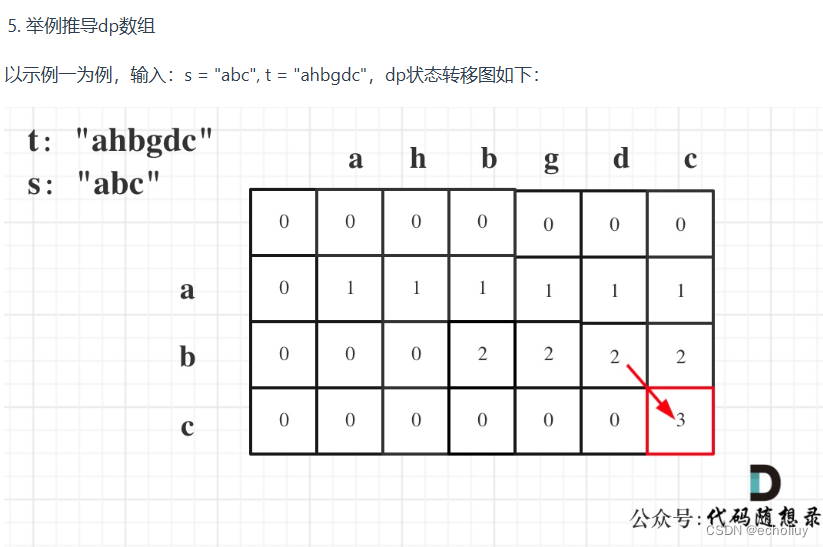
在这里插入图片描述

思路

在这里插入图片描述

在这里插入图片描述
递推顺序：从上到下从左到右

代码：

class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][]dp=new int[s.length()+1][t.length()+1];
        for(int i=1;i<=s.length();i++){
            for(int j=1;j<=t.length();j++){
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=dp[i][j-1];
                }
            }
        }
        // for(int i=1;i<=s.length();i++){
        //     for(int j=1;j<=t.length();j++){
        //         System.out.print(dp[i][j]);
        //     }
        //     System.out.println();
        // }
        return dp[s.length()][t.length()]==s.length();
    }
}

● 115.不同的子序列

在这里插入图片描述

思路：

dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
在这里插入图片描述

代码：

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        // dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
        for (int i = 0; i < s.length() + 1; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i < s.length() + 1; i++) {
            for (int j = 1; j < t.length() + 1; j++) {
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[s.length()][t.length()];
    }
}