多类分类：
多类是分类算法中的一种，它区别于我们的0，1这样子的二进制分类，它会有多个分类的标签，让我们去取其中的一个。
softmax函数：
softmax回归算法是我们的sigmoid回归的推广。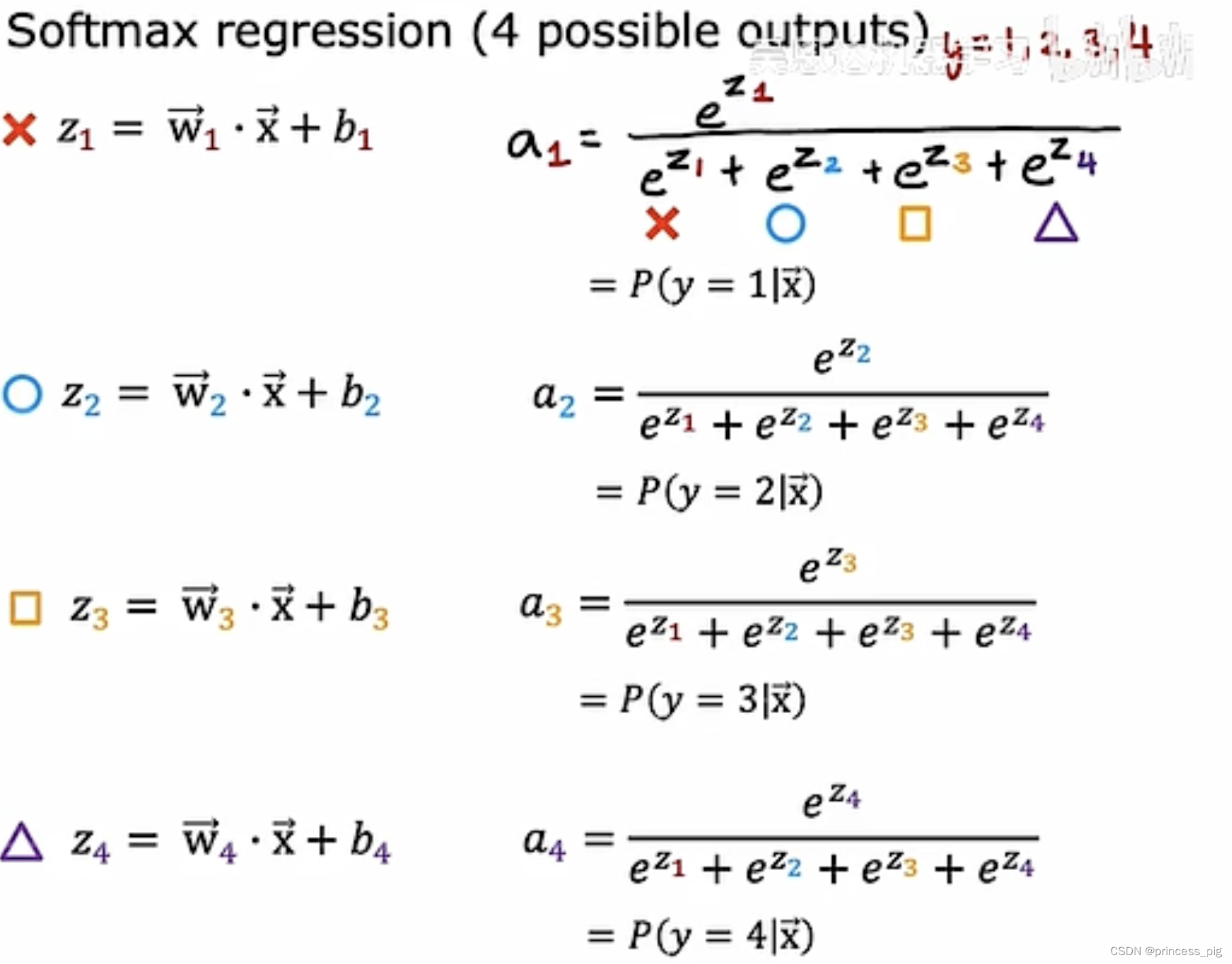
上图就是softmax运行的规范。
左边就是我们的softmax回归函数，而我们的右边则是我们sigmoid回归函数。根据之前的规范了解我们知道了softmax回归算法的各个标签的概率之和为1.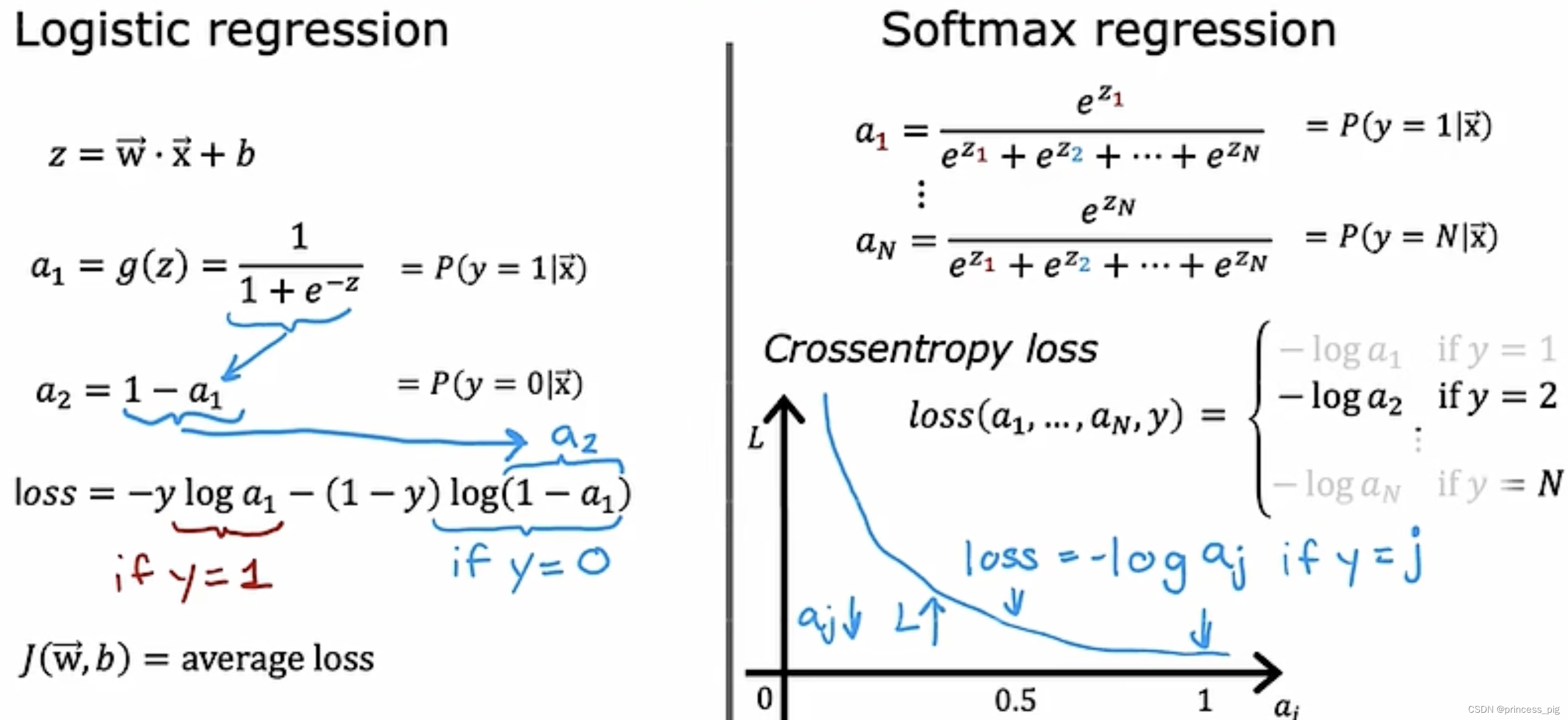 
这就是我们逻辑回归与我们的softmax回归的成本函数的不同，很明显的特点就是我们的softmax函数a的数量会远远大于我们的逻辑回归函数。
在神经网络中使用softmax算法：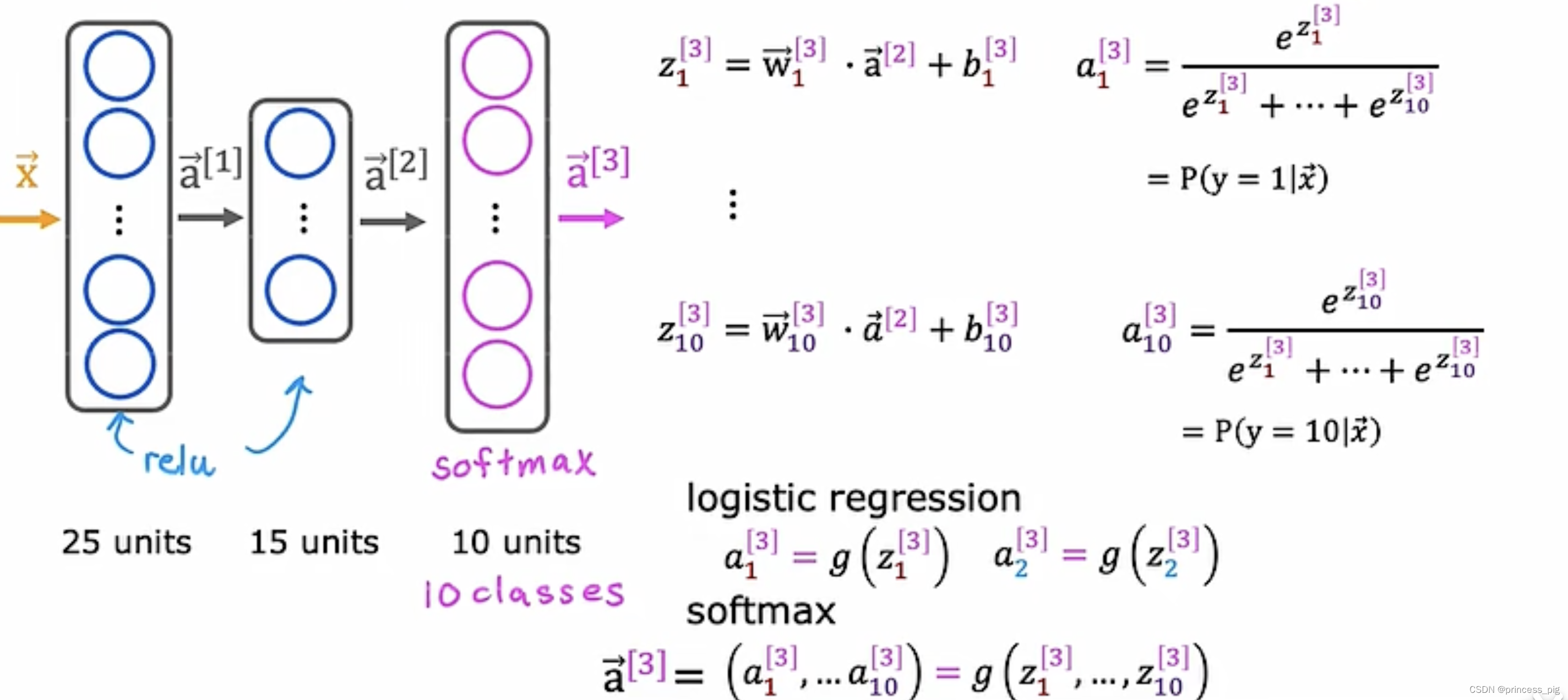 
在我们使用代码表现这个神经网络时，我们的损失函数要用到
SparseCategoricalCrossentropy()
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model.compile(loss=SparseCategoricalCrossentropy())from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model = Sequential([
Dense(units=25, activation="relu"),
Dense(units=15, activation="relu"),
Dense(units=1, activation="softmax")
])
model.compile(loss=SparseCategoricalCrossentropy())
model.fit(X,y,epochs=100)这样我们就可以按照以前的方法训练我们的神经网络了。但实际上，在tensor flow中有更好的版本，我们会在后面学到。
改进softmax算法：
由于我们在tensorflow里使用的数值计算，一直会存在四舍五入的问题，我们的数值并不能得到一个比较准确的答案，于是我们对代码进行了优化。
import tensorflow as tf
import numpy as np
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy
model = Sequential([
Dense(units=25, activation="relu"),
Dense(units=15, activation="relu"),
Dense(units=1, activation="linear")
])
model.compile(loss=SparseCategoricalCrossentropy(from_logits=True))
我们在最后的输出层，不再使用我们的soft Max算法，而是直接用我们的线性激活函数代替它，而在我们的损失算法中加入返回我们的输出值，这样一来，我们从原来的到其中的概率转变为了的到其中的值。但是我们在后面需要得到我们的概率，所以在后面我们需要重新加入一个softmax函数。
model.fit(X,Y,epochs=100)
logits = model(X)
f_x = tf.nn.softmax(logits)当我们遇到多标签分类问题：
这个样子就是我们的多标签分类问题。
当然我们会想到用三个神经网络我们可以分别得到我们的三个不同的值，比如有没有行人，有没有公交车，有没有汽车。我们就改变了一下我们的激活算法来通过一个神经网络同时得到三个值。
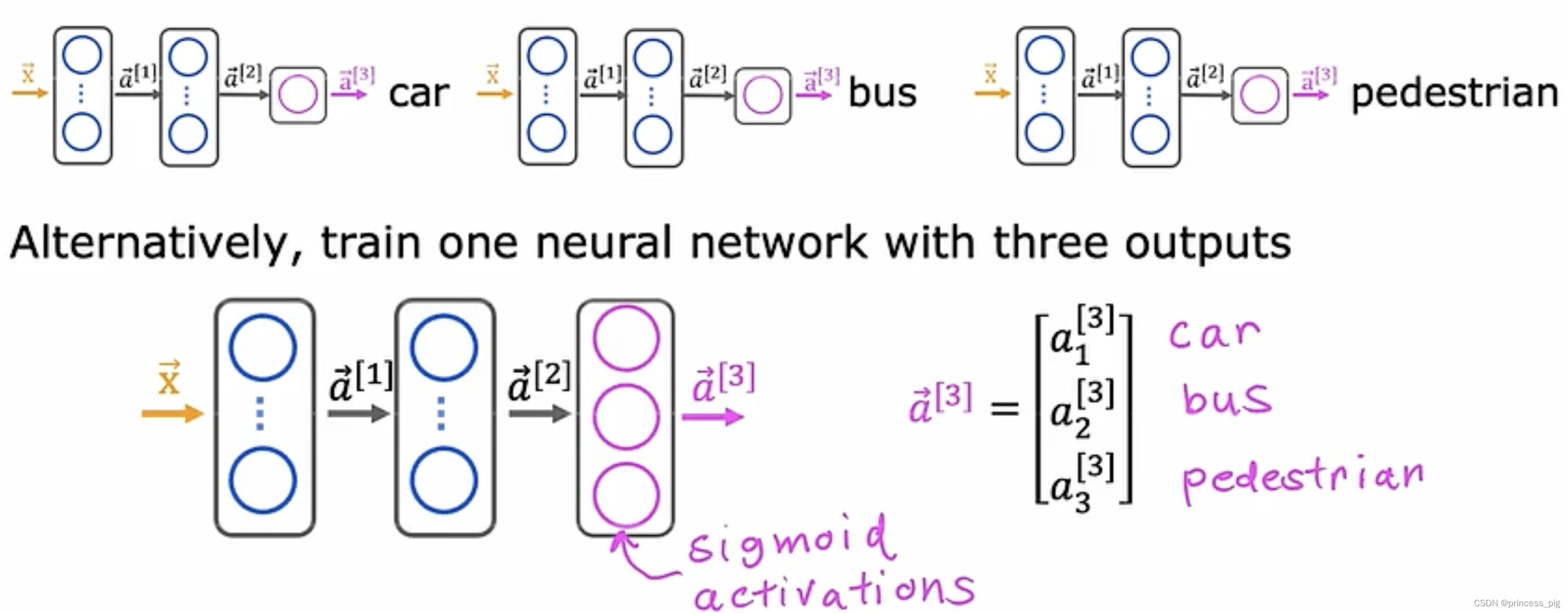很明显，我们把我们的输出层变成三个神经元，然后把我们的激活函数变成sigmoid激活函数 ，这样我们就可以一次性得到我们的三个值。
注意：多类分类和多标签分类不是同一个。
优化算法：
我们在这里要介绍一种比梯度下降更加优化的算法，可以加快我们的梯度下降的速度。
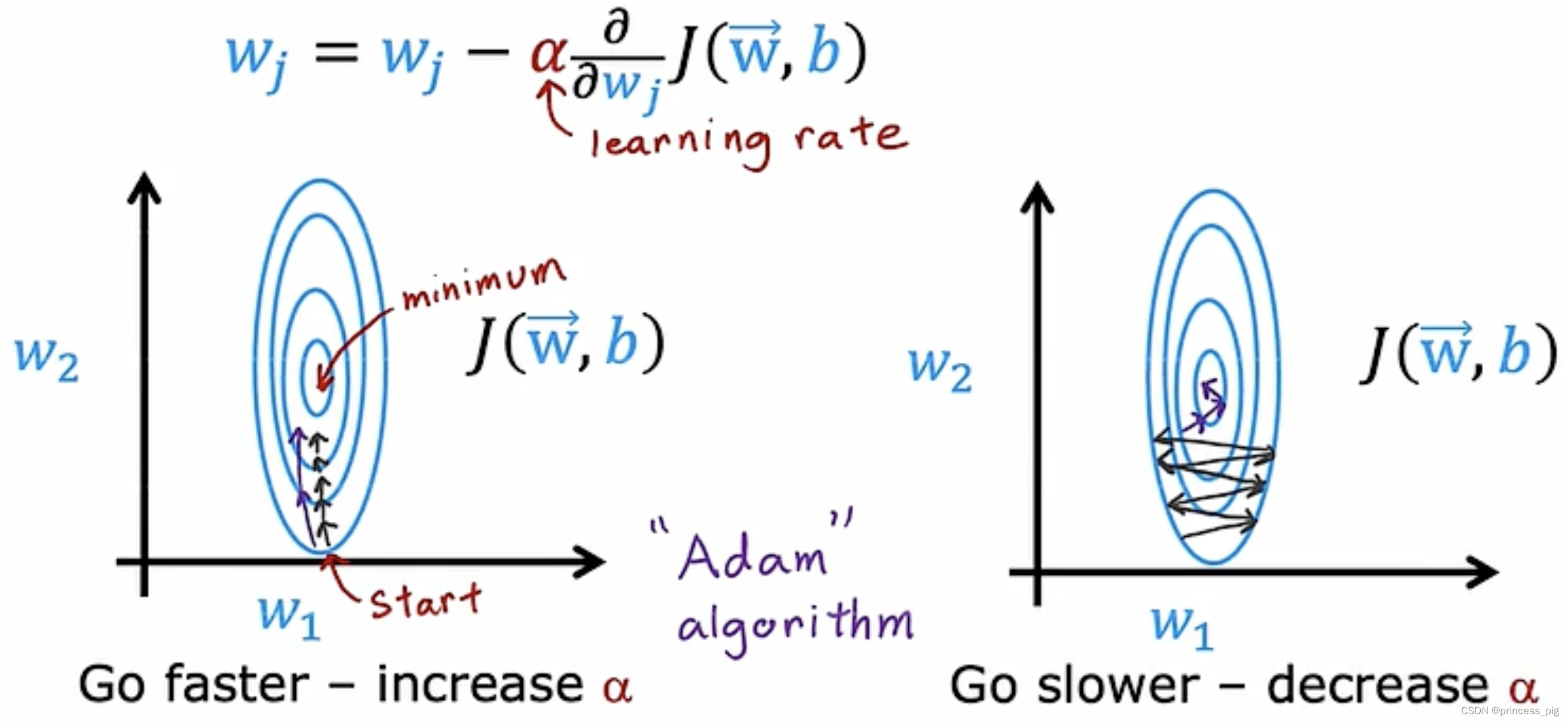我们可以看到，学习率是我们梯度下降的重点，我们要找到一个尽可能快的梯度下降，我们在之前，学习率这个值，我们需要列举多个值，通过比较才能找到一个适合的值，在这里介绍一种新的可以操控
大小的算法，叫做“Adam”算法，它可以自主调节学习率的大小。
有一个很大的优点就是我们的学习率对于不同的值，它的系数并不是相同的，也就是他们并不是全局的，所以会有很多不同的学习率和不同的梯度下降函数一一对应。
它会根据梯度下降的情况，自动调节，当我们的梯度下降正常时，它会增加我们的，从而可以更快的梯度下降，但是当我们的梯度下降一直呈现的是来回震荡，这时它会主动减小
，听上去，这似乎非常不可思议，但是这就是Adam算法的运行原理。
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.losses import SparseCategoricalCrossentropy
from tensorflow.keras.optimizers import Adam
model = Sequential([
Dense(units=25, activation="relu"),
Dense(units=15, activation="relu"),
Dense(units=1, activation="linear")
])
model.compile(optimizer=Adam(learning_rate=1e-3), loss=SparseCategoricalCrossentropy(from_logits=True))我们在这里多加了一个优化器，也就是我们的Adam
model.compile(optimizer=Adam(learning_rate=1e-3), loss=SparseCategoricalCrossentropy(from_logits=True))它是写在我们的损失函数中的，learn_rate指的就是我们的学习率，它是从次。
卷积层(Convolution Layer):
卷积层指的是，我们把一个数据分为多个不同的部分。
这里的卷积层，就是我们的输入层是我们的卷积层，而我们的隐藏层中的神经元，会每个分别扫描不同的部分，而不是全部的卷积层，这也会带来一些优点，第一就是它的运行速度会更快，第二就是所需要的训练的数据更少。
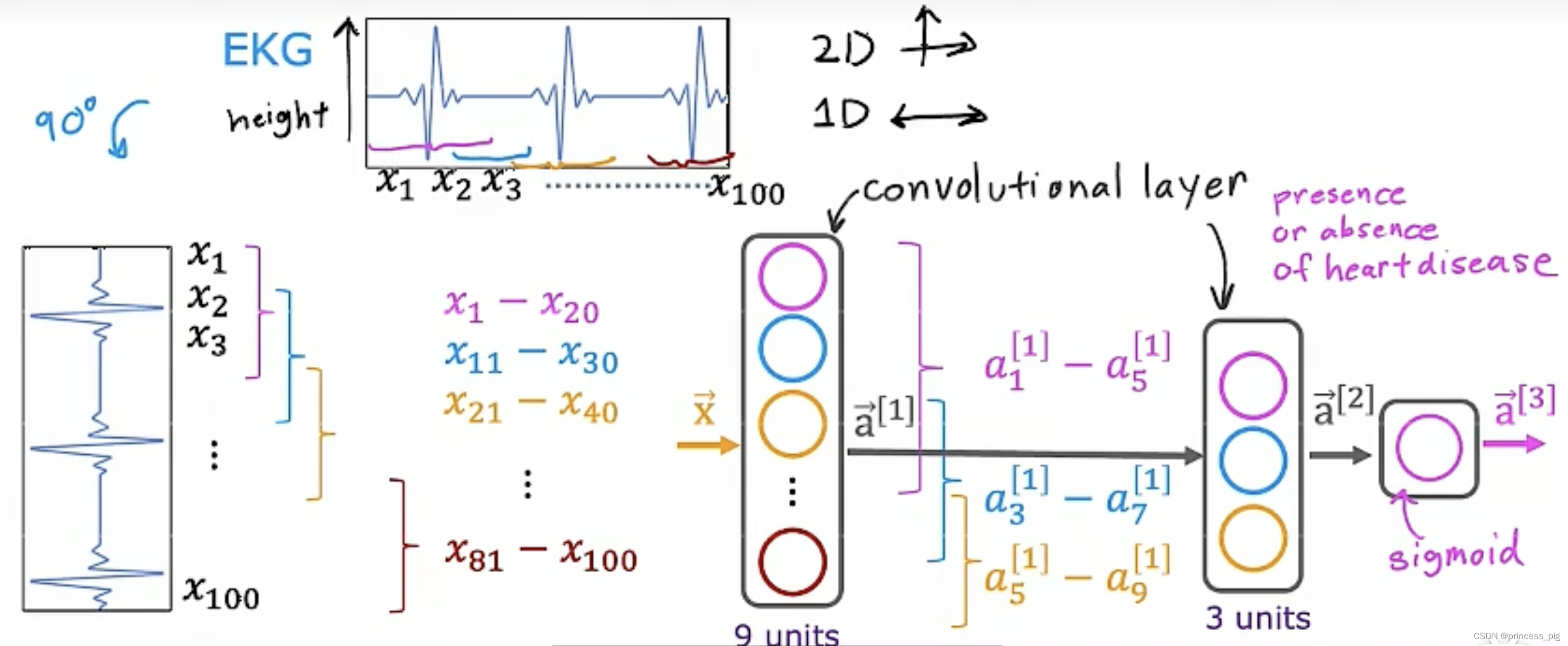
这就是一个典型的卷积层神经网络，我们可以看到我们第一个隐藏层就是一个卷积层，它把我们输入层分为了10个部分，而我们的第二个隐藏层也是一个卷积层，它把我们的第一个隐藏层分为了三个部分，而最后的输出1层，则用了我们的sigmoid函数。
