在了解之前，我们先要了解什么是回文串，什么是回文子串。

回文串和回文子串：

        回文串是指一个字符串正序遍历和反向遍历结果相同的字符串。如 ABBA，正着读反着读结果是一样的。

有了回文串的概念，回文子串的概念也就显而易见了。也就是一个字符串的子字符串是回文串，则该子字符串被称为回文子串。

有了这些概念，我们就能介绍Manacher算法。在我们看实际例题前，我们先来看看什么是Manacher算法。

Manacher算法介绍：

Manacher算法是一个用来查找一个字符串中的最长回文子串(不是最长回文序列)的线性算法。它的优点就是把时间复杂度为O(n^2)的暴力算法优化到了O(n)。

既然是一个寻找字符串的最长回文子串，我们就能想到一种暴力的解法：通过从一个字符串中每个字符的位置开始，向两边扩展，一次一位。当左右指针相对应的字符相同时，那么我们就初步得到了一个回文子串。当我们对整个字符串都进行这样的操作时，我们就能得到最长的回文子串。

这样做的时间复杂度是O(n^2)，也是我们想要优化的对象。

下面放出例题和我们通过暴力的解法的代码：

例题：

给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

代码：

class Solution {
    public String longestPalindrome(String s) {
        int len = s.length();
        String max = s.substring(0,1);
        for(int i=0;i<len-1;i++){
            String odd = new String();
            String even = new String();
            if(s.charAt(i)==s.charAt(i+1)) even = extend(s,i,i+1);
            odd = extend(s,i,i);
            if(odd.length() > max.length()) max = odd;
            if(even.length() > max.length()) max = even;
        }
        return max;
    }
    public String extend(String s,int l,int r){
        int len = s.length();
        String ans = new String();
        while(l>=0 && r<s.length()){
            if(s.charAt(l) == s.charAt(r)){
                if(l==r) ans+=s.charAt(l);
                else{
                    ans = s.charAt(l)+ans;
                    ans = ans + s.charAt(r);
                }
                l--;
                r++;
            }
            else{
                break;
            }
        }
        return ans;
    }
}

当我们遇到ABA这样的字符串是，我们直接扩展得到的结果是正确的131。但是当遇到ABBA这样的偶数长度是，我们得到的结果却是1111，显然这样是错误的。因此，我们对此专门做了分类讨论：

当此处的字符与下一个相同时，我们扩展是从这两个同时扩展的。也就是解决了偶数的问题。‘

当此处的字符与下一个不相同的时候，我们将会从当前的字符直接开始扩展，也就是奇数的问题。

这样做虽然解决了找寻最长回文子串的问题，但是我们会发现每次向外扩展就是O(N)的时间复杂度。每次从一个字符开始向外扩展，也就是一共花费O(N^2)的时间复杂度。

那么有没有更好的方法呢？下面来介绍Manacher算法

Manacher算法：

首先我们要解决的是将麻烦的奇偶情况分类讨论的问题。我们显然可知，偶数的情况相较于奇数的情况更加复杂，因为奇数只需要从此处开始向两边扩展即可。因此我们要想办法将偶数串变成奇数串，同时不影响判断。所以我们需要预处理。

预处理：

假设一个字符串长度为n,无论n是奇是偶，2*n+1的结果一定是奇数，这是毋庸置疑的。所以我们只需将原字符串长度变成2n+1即可。在不影响原串的前提下，我们需要插入n+1个无关字符。插在哪里不影响呢？当然是间隙之间。比如插入'*' ,'$' ,'#' 这种无关字符。这样一来，我们就得到了一个奇数长度的字符串。

Manacher算法核心：

为了介绍Manacher算法，我们在此需要引入几个概念：

Manacher字符串：经过Manacher预处理的字符串
回文半径：回文字符串的中心字符到两端距离。

最右回文边界R：在遍历字符串时，每个字符遍历出的最长回文子串都会有个右边界，而R则是所有已知右边界中最靠右的位置，也就是说R的值是只增不减的。

回文中心C：取得当前R的第一次更新时的回文中心。由此可见R和C时伴生的。

半径数组：这个数组记录了原字符串中每一个字符对应的最长回文半径。

## 此处因为Manacher字符串长度是 2n+1 ，因此它的半径数组记录的其实是原字符串回文子串的回文直径，也就是回文子串的长度。

初始化 R C均为-1，然后从0处遍历字符串。同时创建半径数组。这里有点与概念相差的小偏差，就是R实际是最右边界位置的右一位。因为在计算时R包含了C的位置，导致pArr[i]+i重复计算了一次i的位置。

这时会遇到三种情况：

此处参考了 https://www.cnblogs.com/cloudplankroader/p/10988844.html 的图片和思想。

1️⃣ i > R ，也就是i在R外，此时没有什么花里胡哨的方法，直接暴力匹配，此时记得看看C和R要不要更新。

2️⃣ i <= R，也就是i在R内，此时分三种情况，在讨论这三个情况前，我们先构建一个模型

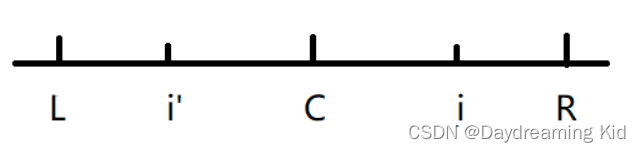
L是当前R关于C的对称点，i'是i关于C的对称点，可知 i' = 2*C - i，并且我们会发现，i'的回文区域是我们已经求过的，从这里我们就可以开始判断是不是可以进行加速处理了

情况1：i'的回文区域在L-R的内部，此时i的回文直径与 i' 相同，我们可以直接得到i的回文半径，下面给出证明

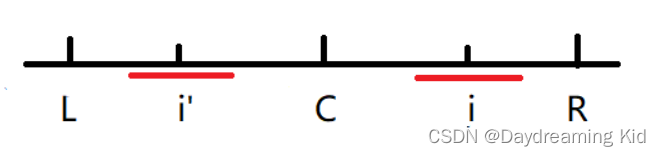
红线部分是 i' 的回文区域，因为整个L-R就是一个回文串，回文中心是C，所以i形成的回文区域和i'形成的回文区域是关于C对称的。

情况2：i'的回文区域左边界超过了L，此时i的回文半径则是i到R,下面给出证明

 

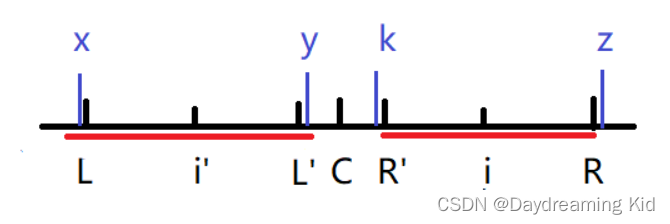
首先我们设L点关于i'对称的点为L'，R点关于i点对称的点为R'，L的前一个字符为x，L’的后一个字符为y，k和z同理，此时我们知道L - L'是i'回文区域内的一段回文串，故可知R’ - R也是回文串，因为L - R是一个大回文串。所以我们得到了一系列关系，x = y，y = k，x != z，所以 k != z。这样就可以验证出i点的回文半径是i - R。

情况3：i' 的回文区域左边界恰好和L重合，此时i的回文半径最少是i到R，回文区域从R继续向外部匹配，下面给出证明

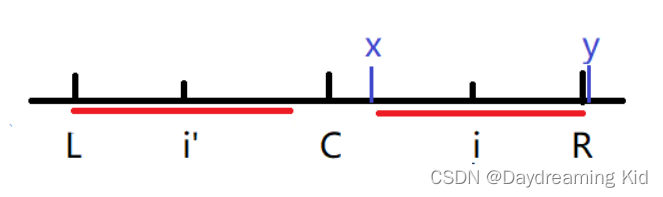
因为 i' 的回文左边界和L重合，所以已知的i的回文半径就和i'的一样了，我们设i的回文区域右边界的下一个字符是y，i的回文区域左边界的上一个字符是x，现在我们只需要从x和y的位置开始暴力匹配，看是否能把i的回文区域扩大即可。

总结一下，Manacher算法的具体流程就是先匹配 -> 通过判断i与R的关系进行不同的分支操作 -> 继续遍历直到遍历完整个字符串

 简单来说，我们需要在暴力算法的基础上利用到以前的结果。如果i<R，那么说明还在范围内，由之前的结果作参考，遍历的范围小。否则只能从1开始逐步遍历。

class Solution {
    public String longestPalindrome(String s) {
        int len = s.length();
        char[] tchs = s.toCharArray();
        char[] chs = new char[tchs.length*2+1];
        int idx = 0;
        for(int i=0;i<chs.length;i++){
            chs[i] = (i & 1) == 1 ? tchs[idx++] : '#';
        }
        int[] pArr = new int[chs.length];
        int R = -1;
        int C = -1;
        int max = Integer.MIN_VALUE;
        int index = -1;
        for(int i=0;i<chs.length;i++){
            pArr[i] = i < R ? Math.min(pArr[2*C-i],R-i) : 1;
            while(i-pArr[i] >= 0 && i+pArr[i]<chs.length){
                if(chs[i+pArr[i]] == chs[i-pArr[i]]){
                    pArr[i]++;
                }else{
                    break;
                }
            }
            if(i+pArr[i] > R){
                R = i + pArr[i];
                C = i;
            }
            if(pArr[i] >= max){
                max = pArr[i];
                index = i;
            }
        }
        String ans = new String();
        for(int i=index-max+1;i<=index+max-1;i++){
            if(chs[i] != '#') ans += chs[i];
        }
        return ans;
    }
}

当我们的 i 还在最右侧的内部时，我们只需要从

Math.min(pArr[2*C-i],R-i)

中的最小值开始遍历就行了，很好理解，此处不展开。就是上面的3种情况。否则只能从1重新开始。遍历结束后，如果现有的范围已经超过原R，扩展R同时改变C为当前的C。