思维链(Chain of Thought,CoT)
**CoT 提示过程是一种大模型提示方法,它鼓励大语言模型解释其推理过程。**思维链的主要思想是通过向大语言模型展示一些少量的 exapmles,在样例中解释推理过程,大语言模型在回答提示时也会显示推理过程。这种推理的解释往往会引导出更准确的结果。

1.零样本思维链(Zero Shot Chain of Thought,Zero-shot-CoT)
零样本思维链(Zero Shot Chain of Thought,Zero-shot-CoT)提示过程是对 CoT prompting 的后续研究,引入了一种非常简单的零样本提示。他们发现,通过在问题的结尾附加“Let’s think step by step”这几个词,大语言模型能够生成一个回答问题的思维链。从这个思维链中,他们能够提取更准确的答案。

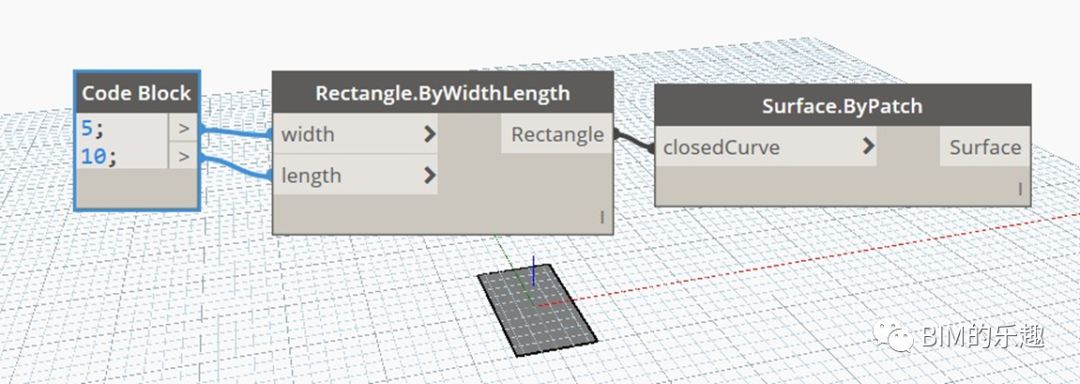
从技术上讲,完整的零样本思维链(Zero-shot-CoT)过程涉及两个单独的提示/补全结果。在下图中,左侧生成一个思维链,而右侧接收来自第一个提示(包括第一个提示本身)的输出,并从思维链中提取答案。这个第二个提示是一个自我增强的提示。

2.多数投票提高CoT性能——自洽性(Self-consistency)
Self-Consistency Improves Chain of Thought Reasoning in Language Models.
这篇文章几乎用的和 CoT 完全一样的数据集和设置,主要改进是对答案进行了多数投票(majority vote),并且发现其可以显著地提高思维链方法的性能。
文章提出的方法叫自洽性(Self-consistency),是对 CoT 的一个补充,它不仅仅生成一个思路链,而是生成多个思路链,然后取多数答案作为最终答案。

3.LtM (Least to Most prompting)提示
最少到最多提示过程 (Least to Most prompting, LtM) 将思维链提示过程 (CoT prompting) 进一步发展,首先将问题分解为子问题,然后逐个解决。它是受到针对儿童的现实教育策略的启发而发展出的一种技术。
与思维链提示过程类似,需要解决的问题被分解成一组建立在彼此之上的子问题。在第二步中,这些子问题被逐个解决。与思维链不同的是,先前子问题的解决方案被输入到提示中,以尝试解决下一个问题。
context + 子问题 + 子问题解题过程 + 子问题答案 + 最终问题,然后让模型去生成解题过程和正确答案,那么这一步也是用 CoT 来做的。


4.Flan-PaLM/T5:CoT + Finetuning
Scaling Instruction-Finetuned Language Models
总结一下,这篇工作提出了 Flan 的微调框架,核心有四点:
- 统一的输入输出格式(4种类型)
- 引入 CoT (chain-of-thought)
- 大幅提高任务数量
- 大幅提高模型体积
实现了用一个模型来解决超过 1800 种几乎全部的 NLP 任务,通过较低的成本,极大发掘了现有语言模型的泛化性能,让大家看到了通用模型的希望。


5.提升小模型的推理能力:Fine-tune-CoT
Fine-tune-CoT 的核心思想是采用 Zero-Shot-CoT 生成我们的问答数据,然后使用温度 T 采样(也可以用 Top-k 采样),以此生成尽可能多的数据,然后再进行 Fine-tune。
其实就是使用不同的温度参数 T 采样,用 ChatGPT 这样的大模型生成 CoT 数据,然后再用小模型进行 Fine-tune。
CoT的局限性
首先,思维链必须在模型规模足够大时才能涌现。
在 Jason Wei 等的研究中,PaLM 在扩展到 540B 参数时,与思维链提示结合,才表现出了先进的性能。一些小规模模型,思维链并没有太大的影响,能力提升也不会很大。
谷歌大脑的研究人员认为,策略问题需要大量的世界知识,而小型模型没有足够的参数来记忆这些世界知识,所以也不太可能产生正确的推理步骤。
但问题是,能落地到产业的模型,规模必然不会太大,思维链拆解了更多的步骤、用到更多的计算资源,相当于更加耗费脑力,很多研究机构和企业是负担不起 175B 参数以上的大模型。
所以思维链必须要探索,如何在较小的模型中进行推理,降低实际应用的成本。
其次,思维链的应用领域是有限的。
目前,思维链只是在一些有限的领域,比如数学问题,五个常识推理基准(CommonsenseQA,StrategyQA,Date Understanding 和 Sports Understanding 以及 SayCan)上显现出作用,其他类型的任务,像是机器翻译,性能提升效果还有待评估。
而且,相关研究用到的模型(GPT-3 API)或数据集,都是半公开或不公开的,这就使其难以被复现和验证。严谨来看,思维链的效果还需要被进一步探索,才能下定论。
此外,即使有思维链提示,大语言模型依然不能解决小学水平的数学问题。
没有思维链,数学推理是指定不行。但有了思维链,大语言模型也可能出现错误推理,尤其是非常简单的计算错误。Jason Wei 等的论文中,曾展示过在 GSM8K 的一个子集中,大语言模型出现了 8% 的计算错误,比如6 * 13 = 68(正确答案是78)。
这说明,即使有了思维链,大语言模型还是没有真正理解数学逻辑,不知道加减乘除的真实意义,只是通过更精细的叠加来“照葫芦画瓢”,所以,对于有精确要求的任务,还要进一步探索新的技术。