文章目录
- 引言
- 一、最小二乘法的基本原理
- 二、最小二乘法的计算过程
- 建立模型
- 确定目标函数
- 求解模型参数
- 模型检验
- 三、最小二乘法的优缺点
- 优点
- 原理简单易懂
- 统计特性优良
- 适用范围广泛
- 缺点
- 对异常值敏感
- 假设条件较多
- 四、最小二乘法在实际应用中的案例
- 五、如何克服最小二乘法的局限性问题
- 1 处理异常值和噪声数据:
- 使用稳健回归(Robust Regression)
- 数据清洗和预处理
- 2 选择更合适的模型:
- 3 正则化技术:
- 岭回归(Ridge Regression)
- Lasso回归
- 4 特征选择和特征工程
- 5 交叉验证和模型评估
- 6 考虑样本权重:
- 7 利用先验知识:
- 8 使用集成学习方法:
- 9 探索其他优化算法:
- 五、总结与展望
引言
最小二乘法是一种数学优化技术,它通过最小化误差的平方和来寻找数据的最佳函数匹配。这种方法在回归分析中得到了广泛应用,其目的是找到一条曲线,使得所有观测数据到这条曲线的垂直距离(即误差)的平方和最小。最小二乘法不仅简单易懂,而且具有优良的统计特性,因此在实际应用中受到了广泛的重视和应用。
一、最小二乘法的基本原理
最小二乘法的基本原理是通过最小化残差平方和来确定模型参数。残差是指观测值与模型预测值之间的差值。当观测值与模型预测值之间的误差越小,说明模型的拟合效果越好。因此,最小二乘法通过最小化所有观测值与模型预测值之间的残差平方和,来得到最佳的模型参数。
在回归分析中,我们通常使用最小二乘法来估计回归系数。回归系数反映了自变量对因变量的影响程度。通过最小二乘法得到的回归系数,可以使得模型的预测值与观测值之间的残差平方和最小。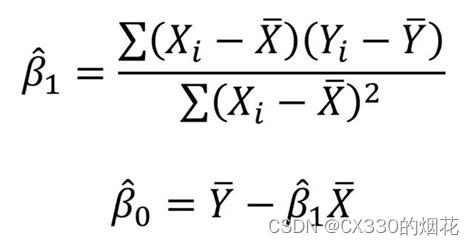
二、最小二乘法的计算过程
最小二乘法的计算过程主要包括以下几个步骤:
建立模型
根据问题的实际背景和需要,选择合适的自变量和因变量,并建立相应的数学模型。
确定目标函数
将模型的残差平方和作为目标函数,即需要最小化的函数。
求解模型参数
通过求解目标函数的最小值,得到模型的参数值。这个过程通常需要用到微积分和线性代数的知识。
模型检验
对得到的模型进行检验,包括拟合优度检验、残差分析等,以评估模型的可靠性和有效性。
三、最小二乘法的优缺点
优点
原理简单易懂
最小二乘法基于直观的残差最小化原理,易于理解和应用。
统计特性优良
最小二乘法得到的模型参数具有优良的统计特性,如线性性、无偏性和最小方差性等。
适用范围广泛
最小二乘法可以应用于线性回归、非线性回归等多种回归分析中,具有广泛的适用性。
缺点
对异常值敏感
当数据中存在异常值时,最小二乘法的结果可能会受到较大的影响,导致模型的预测精度下降。
假设条件较多
最小二乘法在应用时通常需要满足一些假设条件,如误差项的独立性、正态性等。如果这些假设条件不满足,可能会影响模型的准确性和可靠性。
四、最小二乘法在实际应用中的案例
import numpy as np
import matplotlib.pyplot as plt
# 假设我们有一些数据点
x = np.array([0, 1, 2, 3, 4, 5])
y = np.array([0, 0.8, 2.2, 2.8, 3.9, 5.1])
# 使用NumPy的polyfit函数进行线性拟合,这里1表示我们想要拟合一个一次多项式(即线性拟合)
slope, intercept = np.polyfit(x, y, 1)
# 输出拟合得到的斜率和截距
print(f"斜率: {slope}, 截距: {intercept}")
# 创建拟合的直线方程
line = slope * x + intercept
# 使用matplotlib绘制原始数据点和拟合的直线
plt.scatter(x, y, color='blue', label='原始数据')
plt.plot(x, line, color='red', label='拟合直线')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
在这个例子中,np.polyfit函数执行了最小二乘拟合,返回了拟合直线的斜率和截距。然后,我们使用这些参数创建了一个表示拟合直线的数组,并使用matplotlib库将原始数据点和拟合的直线绘制出来。
请注意,这个例子假设你要进行的是线性拟合。如果你想要进行非线性拟合,你可能需要使用更复杂的函数或者方法,比如SciPy的curve_fit函数。
最小二乘法在实际应用中有着广泛的应用。例如,在经济学领域,我们可以利用最小二乘法来估计需求函数或供给函数的参数;在生物学领域,我们可以利用最小二乘法来分析生物种群的数量变化与环境因素之间的关系;在工程技术领域,我们可以利用最小二乘法来进行数据拟合和预测等。
以一个简单的线性回归为例,假设我们有一组关于房价和房屋面积的数据,我们希望建立一个线性回归模型来预测房价。通过最小二乘法,我们可以得到回归直线的斜率和截距,从而得到房价与房屋面积之间的线性关系。这样,我们就可以根据房屋的面积来预测其可能的售价。
五、如何克服最小二乘法的局限性问题
要克服最小二乘法的局限性问题,可以从多个方面入手。以下是一些建议和方法:
1 处理异常值和噪声数据:
使用稳健回归(Robust Regression)
这种方法对异常值不太敏感,可以减小异常值对回归模型的影响。
数据清洗和预处理
通过去除或修正异常值,以及通过平滑技术减少噪声,可以提高最小二乘法的准确性。
2 选择更合适的模型:
1.如果数据呈现非线性关系,尝试使用多项式回归或其他非线性模型。
2.考虑使用混合效应模型、广义线性模型等更复杂的模型来适应数据的复杂性。
3 正则化技术:
岭回归(Ridge Regression)
通过在损失函数中引入模型参数的L2范数作为惩罚项,来防止过拟合。
Lasso回归
使用L1范数作为惩罚项,它有助于稀疏化模型参数,即减少非零参数的数量。
4 特征选择和特征工程
选择与因变量相关性较强的自变量进行建模。
通过创建新的特征或变换现有特征来改进模型的性能。
5 交叉验证和模型评估
使用交叉验证来选择最佳的模型参数,并评估模型的泛化能力。
结合其他评估指标(如R方值、均方误差等)来全面评价模型的性能。
6 考虑样本权重:
如果不同样本的重要性不同,可以使用加权最小二乘法,为每个样本分配不同的权重。
7 利用先验知识:
如果有关于模型参数的先验知识,可以将其纳入建模过程中,以改进模型的准确性。
8 使用集成学习方法:
通过组合多个最小二乘回归模型(如bagging、boosting等),可以提高模型的稳定性和预测性能。
9 探索其他优化算法:
除了最小二乘法外,还可以探索其他优化算法来求解回归问题,如梯度下降、牛顿法等。
需要注意的是,不同的数据集和问题背景可能需要采用不同的方法来克服最小二乘法的局限性。因此,在实际应用中,需要结合具体情况来选择合适的方法和策略。同时,不断学习和尝试新的技术和方法也是提高模型性能的重要途径。
五、总结与展望
最小二乘法作为一种重要的数学优化技术,在回归分析中发挥着至关重要的作用。它通过最小化残差平方和来确定模型的参数,使得模型的预测值与观测值之间的误差最小。虽然最小二乘法存在一些缺点和不足,但在实际应用中,我们可以结合具体问题的特点和需求,选择适当的方法和技巧来克服这些缺点,提高模型的准确性和可靠性。
随着大数据时代的到来,数据分析和挖掘的需求越来越强烈。最小二乘法作为一种基础的数据分析工具,将在未来的数据分析领域继续发挥重要作用。同时,随着计算机技术的不断发展,我们可以利用更加高效的算法和工具来实现最小二乘法的计算和优化,进一步提高模型的性能和效率。