LeetCode091之解码方法（相关话题：动态规划）

news2024/9/30 7:22:05

题目描述

一条包含字母 A-Z 的消息通过以下映射进行了编码：

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

要解码已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：

"AAJF" ，将消息分组为 (1 1 10 6)
"KJF" ，将消息分组为 (11 10 6)

注意，消息不能分组为 (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。

给你一个只含数字的非空字符串 s ，请计算并返回解码方法的总数。

题目数据保证答案肯定是一个 32 位 的整数。

示例 1：

输入：s = "12"
输出：2
解释：它可以解码为 "AB"（1 2）或者 "L"（12）。

示例 2：

输入：s = "226"
输出：3
解释：它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

示例 3：

输入：s = "06"
输出：0
解释："06" 无法映射到 "F" ，因为存在前导零（"6" 和 "06" 并不等价）。

解题思路

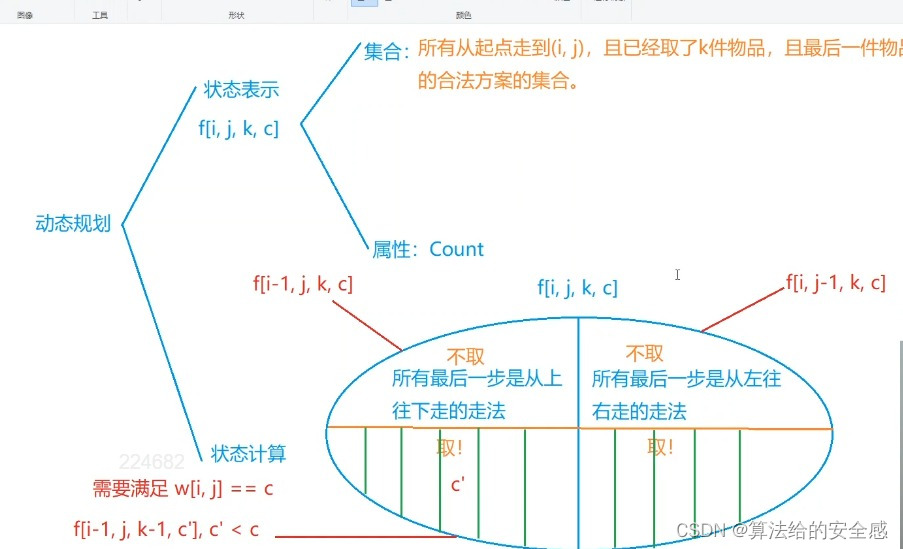
状态表示：f[i]表示前i个数字一共有多少种解码方式，那么，f[n]就表示前n个数字一共有多少种不同的解码方式，即为答案。

状态计算：

设定字符串数组为s[](数组下标从1开始)，考虑最后一次解码方式，因此对于第i - 1和第i 个数字，分为两种决策：

1、如果s[i]不为0，则可以单独解码s[i]，由于求的是方案数，如果确定了第i个数字的翻译方式，那么解码前i个数字和解码前i - 1个数的方案数就是相同的，即f[i] = f[i - 1]。(s[]数组下标从1开始)

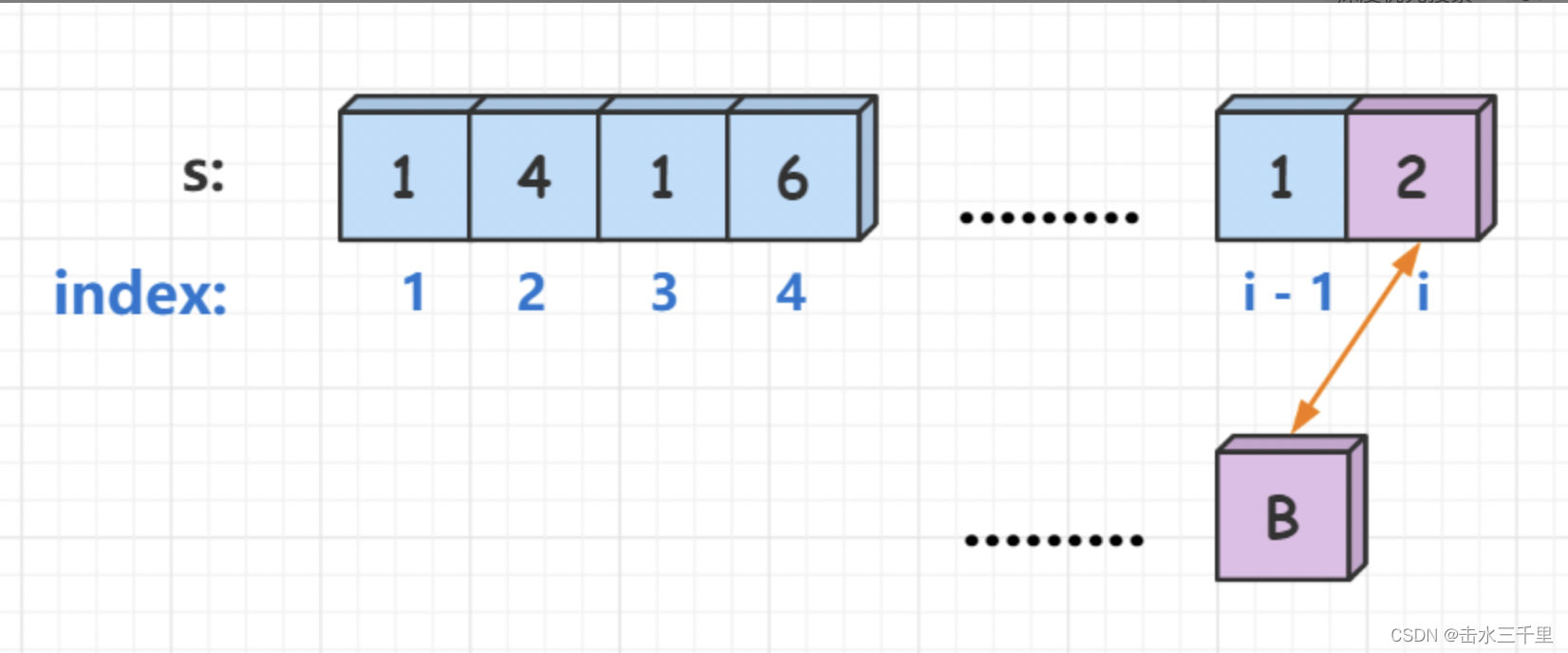
2、将s[i]和s[i - 1]组合起来解码（组合的数字范围在10 ~ 26之间）。如果确定了第i个数和第i - 1个数的解码方式，那么解码前i个数字和解码前i - 2个数的方案数就是相同的，即f[i] = f[i - 2]。(s[]数组下标从1开始)

最后将两种决策的方案数加起来，因此，状态转移方程为： f[i] = f[i - 1] + f[i - 2]。

边界条件：

f[0] = 1，解码前0个数的方案数为1。

为什么解码前0个数的方案数是1？

f[0]代表前0个数字的方案数，这样的状态定义其实是没有实际意义的，但是f[0]的值需要保证边界是对的，即f[1]和f[2]是对的。比如说，第一个数不为0，那么解码前1个数只有一种方法，将其单独解码，即f[1] = f[1 - 1] = 1。解码前两个数，如果第1个数和第2个数可以组合起来解码，那么f[2] = f[1] + f[0] = 2 ，否则只能单独解码第2个数，即f[2] = f[1] = 1。因此，在任何情况下f[0]取1都可以保证f[1]和f[2]是正确的，所以f[0]应该取1。

代码实现

class Solution {
    public int numDecodings(String s) {
        int n = s.length();
        int[] f = new int[n + 10];
        f[0] = 1;
        for(int i = 1; i <= n;i ++)
        {
            if(s.charAt(i - 1) != '0') f[i] = f[i - 1]; //单独解码s[i - 1]
            if(i >= 2)
            {
                int t = (s.charAt(i - 2) - '0') * 10 + s.charAt(i - 1) - '0';
                if(t >= 10 && t <= 26) f[i] += f[i - 2]; 
               //将s[i - 2] 和 s[i - 1]组合解码
               //f[i] = f[i] + f[i - 2]; 的原因是f[i] 在上一步已经用f[i - 1]赋值过了
               //本质要表达的是f[i] = f[i-1] + f[i - 2]
            }
        }
        return f[n];
    }
}