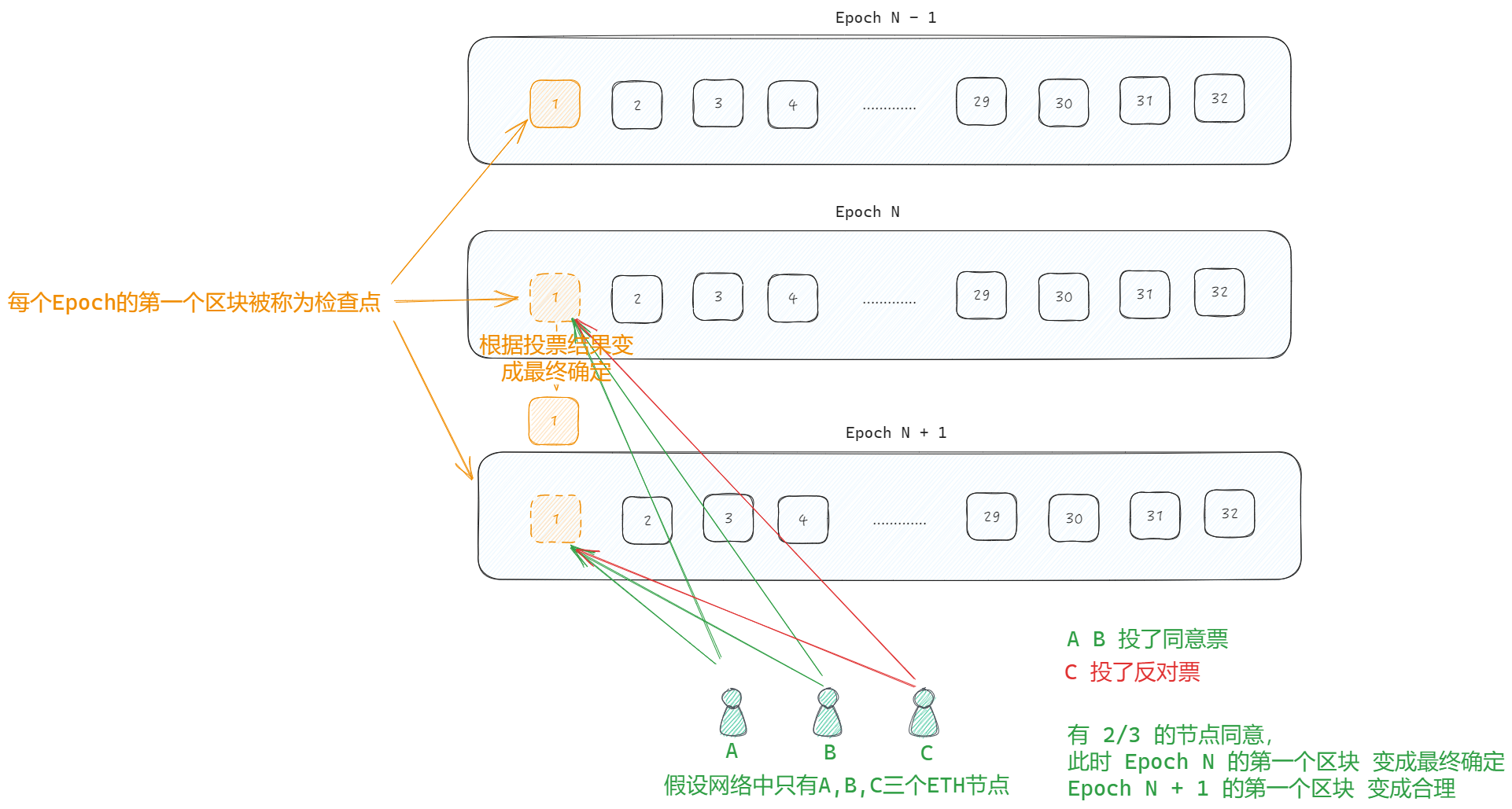
ArcGIS中有相关工具实现多值提取到点的功能，在这里，我将使用R语言进行操作：

library(dplyr)
library(readxl)
library(sf)
library(raster)

setwd("D:/Datasets")
Bio <- stack(paste0("D:/Datasets/Data/worldclim2_1km/",
                            c("wc2.1_30s_bio_1","wc2.1_30s_bio_2",
                              "wc2.1_30s_bio_3","wc2.1_30s_bio_4",
                              "wc2.1_30s_bio_5","wc2.1_30s_bio_6",
                              "wc2.1_30s_bio_7","wc2.1_30s_bio_8",
                              "wc2.1_30s_bio_9","wc2.1_30s_bio_10",
                              "wc2.1_30s_bio_11","wc2.1_30s_bio_12",
                              "wc2.1_30s_bio_13","wc2.1_30s_bio_14",
                              "wc2.1_30s_bio_15","wc2.1_30s_bio_16",
                              "wc2.1_30s_bio_17","wc2.1_30s_bio_18",
                              "wc2.1_30s_bio_19"
                            ),
                            ".tif")
)

dataset <- read_excel("datasets.xlsx")
head(dataset)

# 定义经纬度坐标
longlat<- as.data.frame(dataset[,c(2:3)])
# 将经纬度坐标转换为SpatialPoints对象
coordinates(longlat) <- c("Long", "Lat")
proj4string(longlat) <- CRS("+proj=longlat +datum=WGS84")
#定义转换的投影方式
UTM_Proj <- CRS(st_crs(Bio)$proj4string)
# 将经纬度坐标转换为xy坐标
xy <- spTransform(longlat, UTM_Proj)
# 检查投影坐标系是否一致
st_crs(Bio)$proj4string
st_crs(xy)$proj4string

data_clim<-raster::extract(Bio, xy)
head(data_clim)

这里Bio数据结果如下： 其中地理坐标系为WGS 1984，投影坐标系为WGS 1984 Albers（见crs）

> Bio
class      : RasterStack 
dimensions : 1422, 1185, 1685070, 19  (nrow, ncol, ncell, nlayers)
resolution : 1000, 1000  (x, y)
extent     : 296958.9, 1481959, 2562602, 3984602  (xmin, xmax, ymin, ymax)
crs        : +proj=aea +lat_0=0 +lon_0=105 +lat_1=25 +lat_2=47 +x_0=0 +y_0=0 +datum=WGS84 +units=m +no_defs 
names      : wc2.1_30s_bio_1, wc2.1_30s_bio_2, wc2.1_30s_bio_3, wc2.1_30s_bio_4, wc2.1_30s_bio_5, wc2.1_30s_bio_6, wc2.1_30s_bio_7, wc2.1_30s_bio_8, wc2.1_30s_bio_9, wc2.1_30s_bio_10, wc2.1_30s_bio_11, wc2.1_30s_bio_12, wc2.1_30s_bio_13, wc2.1_30s_bio_14, wc2.1_30s_bio_15, ... 
min values :        3.520833,        5.666667,       19.015659,      585.165588,       17.000000,      -11.500000,       24.199999,       12.566667,       -5.850000,        12.566667,        -5.850000,       533.000000,       109.000000,         2.000000,        41.892853, ... 
max values :        20.31667,        11.91667,        33.88480,      1056.25293,        34.50000,         6.20000,        38.90000,        27.73333,        17.23333,         28.71667,         12.00000,       2296.00000,        368.00000,         62.00000,        111.78159, ... 

注意： dataset中使用的采样点为度分表的小数形式，然而所需要提取的Bio数据为投影坐标系，所以这里需要为dataset采样点定义一个相同的投影坐标系，才能实现采样。