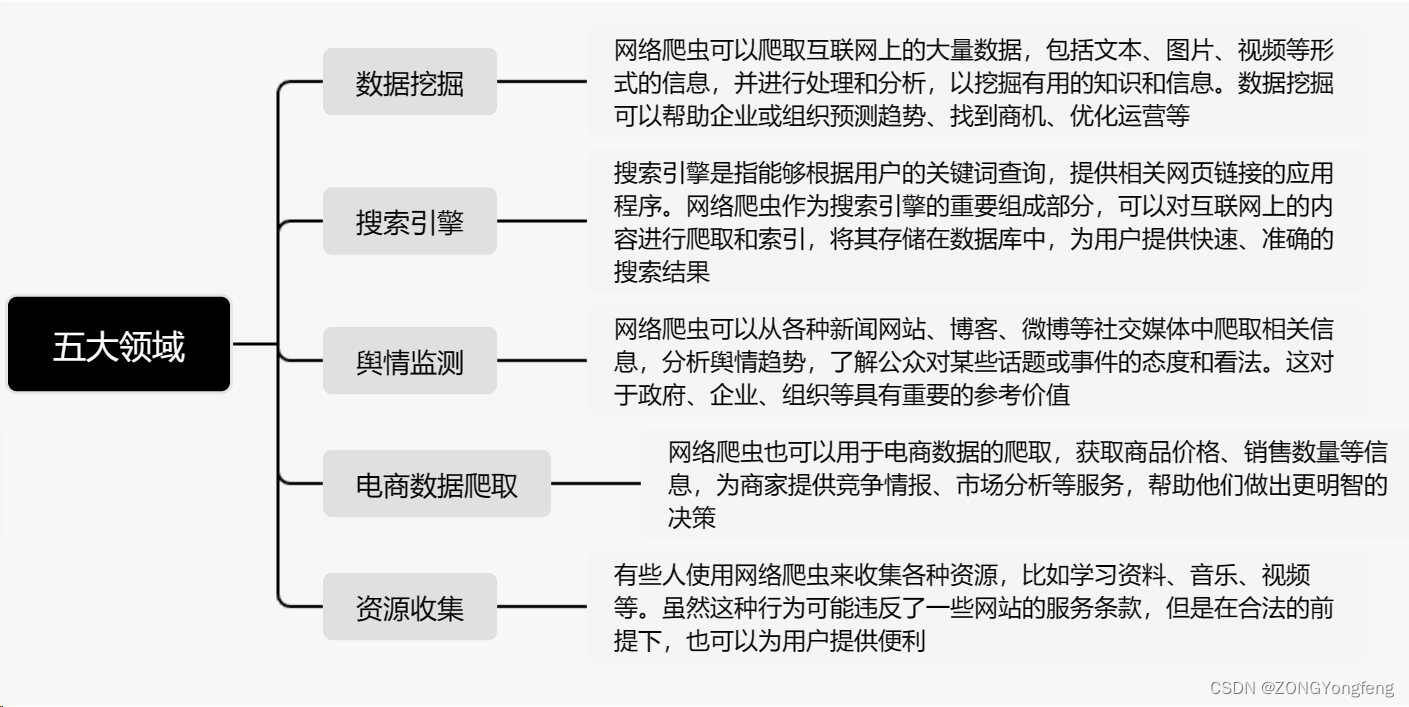
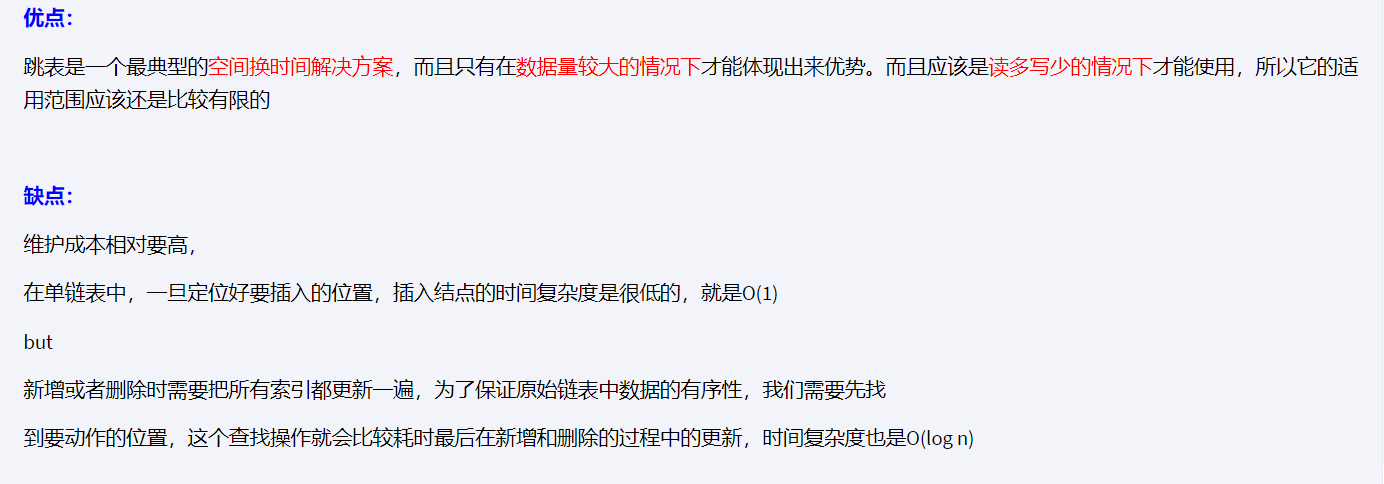
目录

1. 思路

2. 解题方法

3. 复杂度

4. Code

---

题目：

        给你一个字符串 s，找到 s 中最长的回文子串。

        如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"

提示：

• 1 <= s.length <= 1000
• s 仅由数字和英文字母组成

1. 思路

        要找到字符串 s 中的最长回文子串，我们可以尝试不同的方法。一种常见的方法是使用动态规划。我们定义一个二维数组 dp，其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串。根据动态规划的思想，我们可以从长度较短的子串开始，逐步扩展到长度较长的子串，并记录下最长的回文子串。

2. 解题方法

1. 定义一个二维数组 dp，其中 dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串。
2. 初始化 dp 数组，所有长度为 1 的子串都是回文串，相邻字符相同的子串也是回文串。
3. 遍历字符串，根据动态规划的定义填充 dp 数组。
4. 在计算 dp 数组的过程中，记录下最长的回文子串的起始位置和长度。
5. 返回最长的回文子串。

3. 复杂度

• 时间复杂度：O(n^2)，其中 n 是字符串的长度。动态规划需要填充一个二维数组，每个位置需要 O(1) 的时间复杂度。
• 空间复杂度：O(n^2)，需要一个二维数组来存储动态规划的结果。

4. Code

class Solution {
    public String longestPalindrome(String s) {
        if (s == null || s.length() < 1) return "";
        int n = s.length();
        // 定义二维数组 dp，dp[i][j] 表示从索引 i 到索引 j 的子串是否是回文串
        boolean[][] dp = new boolean[n][n];
        int start = 0, maxLength = 1;
        
        // 初始化 dp 数组，所有长度为 1 的子串都是回文串
        for (int i = 0; i < n; i++) {
            dp[i][i] = true;
        }
        
        // 遍历字符串，计算 dp 数组
        for (int len = 2; len <= n; len++) {
            for (int i = 0; i <= n - len; i++) {
                int j = i + len - 1;
                // 如果当前子串的头尾字符相同，并且内部子串也是回文串，则当前子串是回文串
                if (s.charAt(i) == s.charAt(j) && (len == 2 || dp[i + 1][j - 1])) {
                    dp[i][j] = true;
                    // 更新最长回文子串的起始位置和长度
                    if (len > maxLength) {
                        start = i;
                        maxLength = len;
                    }
                }
            }
        }
        // 返回最长回文子串
        return s.substring(start, start + maxLength);
    }
}

        这段代码使用动态规划的方法，实现了找到字符串中最长的回文子串。通过填充一个二维数组 dp，记录从每个位置开始到每个位置结束的子串是否是回文串，并根据动态规划的结果找到最长的回文子串。

欢迎大家后台联系讨论。