一共五道题：
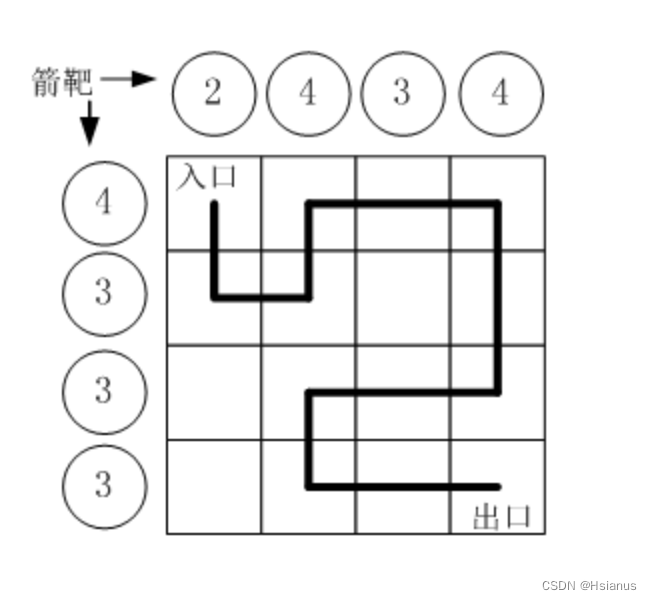
1. PERKET：
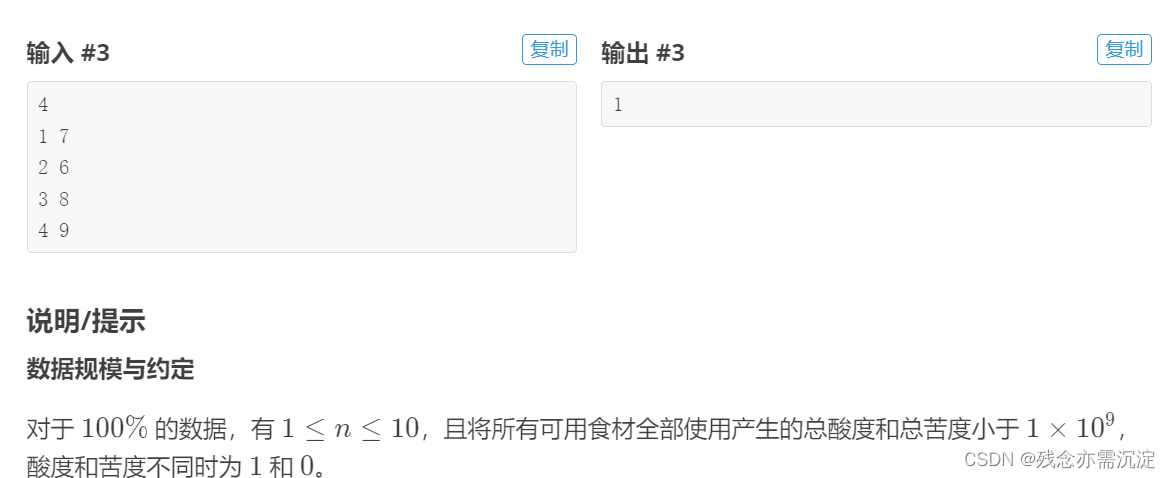
观察容易发现n的值很小，所以我们可以考虑使用dfs的方法进行解答，首先我们可以考虑一共有n种配料，那么我们就可以考虑到可以选择1到n种配料数目，然后基于这个思路我们再对其进行判断当选择几种并且选择哪几种能够得到最小的酸甜度匹配，于是代码就如下：
#include<bits/stdc++.h>
using namespace std;
const int N=50;
int n,ans=1<<20,x=1,y=0;
int a[N],b[N],book[N];
void dfs(int c){
if(c==0){
ans=min(ans,abs(x-y));
return;
}
for(int i=1;i<=n;i++){
if(book[i]){
x*=a[i];
y+=b[i];
--c;
book[i]=0;
dfs(c);
book[i]=1;
++c;
x/=a[i];
y-=b[i];
}
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i];
}
for(int i=1;i<=n;i++){
x*=a[i];
y+=b[i];
}
ans=min(ans,abs(x-y));
for(int i=1;i<=n;i++){
ans=min(ans,abs(a[i]-b[i]));
}
for(int i=2;i<n;i++){
memset(book,1,sizeof(book));
x=1;
y=0;
dfs(i);
}
cout<<ans<<endl;
return 0;
}引入了book数组来标记在dfs过程中已经被使用过的配料，然后先把选择一种和n种配料的情况给算出来并更新最小的ans，接下来再判断当选择的配料数目为2到n-1的时候，对应的最小ans，并利用dfs进行不断更新。
2.迷宫：
这道题目就是最经典和典型的dfs模板题目了，直接上代码吧：
#include<iostream>
#include<cstring>
using namespace std;
int n,m,t;
int startx,starty,p,q;
const int N=10;
int book[50][50],a[50][50];
int ans=0;
void dfs(int x,int y){
if(x==p && y==q){
++ans;
return;
}
int next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
int tx,ty;
for(int i=0;i<=3;i++){
tx=x+next[i][0];
ty=y+next[i][1];
if(tx < 1 || tx > n || ty < 1 || ty > m)
continue;
if(!book[tx][ty] && a[tx][ty]){
book[tx][ty] = 1;
dfs(tx,ty);
if(a[tx][ty]) book[tx][ty]=0;
}
}
}
int main(){
cin >> n >> m >> t;
cin >> startx >> starty >> p >> q;
memset(book,0,sizeof(book));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++)
a[i][j]=1;
}
for(int i=1;i<=t;i++){
int x,y;
cin>>x>>y;
a[x][y]=0;
}
dfs(startx,starty);
cout<<ans<<endl;
return 0;
}利用一个a数组代表是否有陷阱，利用book数组表示对于同一种方案是否有走过同一个格子，在dfs中利用一个二维数组来表示接下来一步的上下左右并进行枚举，不过我至今没有想明白为什么这只能获得70分。
3.借教室：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 1000010;
int n, m;
int w[N];//这个数组用来存储n天中每一天对应的可借出去的教室
int l[N], r[N], d[N];//l和r分别表示对应天数的差分端点，d数组则表示对应需要借出的教室
LL b[N];//当进行二分筛选的时候这一个数组就是拿来进行记录当订单数量为mid的时候每一天需要的教室数量
bool check(int mid)
{
memset(b, 0, sizeof b);
for (int i = 1; i <= mid; i ++ )
{
b[l[i]] += d[i];
b[r[i] + 1] -= d[i];//对端点进行加减
}
for (int i = 1; i <= n; i ++ )
{
b[i] += b[i - 1];
if (b[i] > w[i]) return false;//如果当天的需求大于所能提供的教室数量则说明要求的值在mid的左边
}
return true;
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ )
scanf("%d", &w[i]);
for (int i = 1; i <= m; i ++ )
scanf("%d%d%d", &d[i], &l[i], &r[i]);
int l = 0, r = m;
while (l < r)
{
int mid = l + r + 1 >> 1;//我们的二分求出来的r是最后一份能恰好满足教室需求的订单，r+1则是第一个无法满足的订单，记得右移
if (check(mid)) l = mid;
else r = mid - 1;
}
if (r == m) puts("0");
else printf("-1\n%d\n", r + 1);
return 0;
}
这道题目的方法就是差分加二分，订单的数量越多，那么剩余的空余教室的数量肯定会减少，因此我们考虑使用二分的方法进行查找，对于每一份订单，我们都有一个区间，在这个区间上加上订单所对应的借教室的数量，但是我们会发现题目当中，n和m的极限数据是10的6次方，如果对于每一个订单我们都将从第l天到第r天进行枚举并加上借教室的数量的话会导致tle，所以我们考虑使用差分的方式进行加速处理，这样处理的时间复杂度为O(n+m)logm。
以下是二分的两种模板：
bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
while (l < r)
{
int mid = l + r >> 1;
if (check(mid)) r = mid; // check()判断mid是否满足性质
else l = mid + 1;
}
return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid)) l = mid;
else r = mid - 1;
}
return l;
}
4.分巧克力：
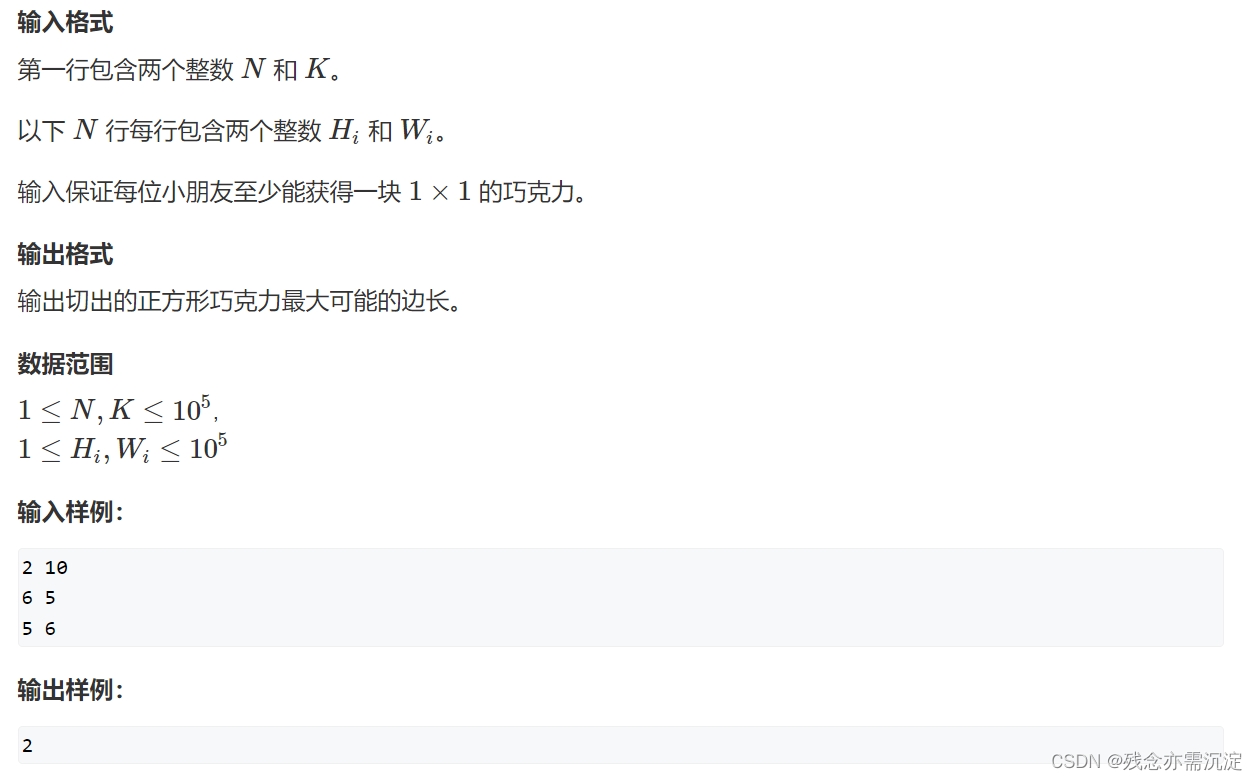这道题目的话 难度比排教室要小很多了，我们可以考虑使用二分来找到所给的巧克力总共可以分成的边长最大的数量大于k的答案，那么我们的代码可以这样去写：
#include<iostream>
using namespace std;
const int N=1e5+100;
int w[N],h[N];
int n,k;
bool pd(int x){
int ans=0;
for(int i=1;i<=n;i++){
ans += (w[i]/x) * (h[i]/x);
}
if(ans>=k) return true;
else return false;
}
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>w[i]>>h[i];
}
int l=1,r=100000;
while(l<r){
int mid=l+r+1>>1;
if(pd(mid)) l=mid;
else r=mid-1;
}
cout<<r<<endl;
return 0;
}5.技能升级
这是一道很难的题目，题解如下：
一定要记得开long long：
#include <iostream>
#include <cmath>
#define N 100005
using namespace std;
int n, m, l = 0, r = 1e6, mid, now, cnt, a[N], b[N];
long long ans;
long long sum (int r, int n, int t) // 求和
{
int l = r - t * (n - 1);
return (long long) (l + r) * n >> 1;
}
bool check (int x)
{
long long res = 0;
for (int i = 1; i <= n; i ++)
{
if (a[i] > x) // 前提条件
{
res += ceil ((double) (a[i] - x) / b[i]);
// 累计第 i 个技能发动的次数
}
}
return res <= m; // 判断是否合法
}
int main ()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++)
{
cin >> a[i] >> b[i];
}
while (l < r) // 二分
{
mid = l + r >> 1;
if (check (mid)) // 如果 x = mid 合法
{
r = mid;
}
else
{
l = mid + 1;
}
}
for (int i = 1; i <= n; i ++)
{
if (a[i] > l) // 前提条件
{
now = ceil ((double) (a[i] - l) / b[i]), cnt += now;
// now 是第 i 个技能发动的次数，cnt 则是总共升级了多少次
ans += sum (a[i], now, b[i]);
// 总升级攻击力累加上右端点为 a[i]，项数为 now，公差为 b[i] 的等差数列和
}
}
cout << ans + (long long) l * (m - cnt); // 答案还要记得加上那些等于 l 的攻击力增加
return 0;
}也可以用另一种二分模板，代码如下：
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,ans;
const int N=1e3+100;
int a[N],d[N];
int sum(int An,int n,int dx){
int A1=An-(n-1)*dx;
return n*(A1+An)/2;
}
bool check(int x){
int cnt=0;
for(int i=1;i<=n;i++){
if(a[i]>x) cnt += ceil( (double)(a[i]-x) / d[i]);
}
return cnt>=m;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int l=0,r=1e6;
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i]>>d[i];
}
while(l<r){
int mid=l+r+1>>1;
if(check(mid)) l=mid;
else r=mid-1;
}
int cnt=0;
for(int i=1;i<=n;i++){
if(a[i]>r){
int now=ceil((double)(a[i]-r)/d[i]);
cnt+=now;
ans += sum(a[i],now,d[i]);
}
}
cout<<ans+(m-cnt)*r;
return 0;
}感谢您的观看。
![练习 6 Web [极客大挑战 2019]HardSQL](https://img-blog.csdnimg.cn/direct/eee8d8cb19d64d819016066c5c7727cb.png)
