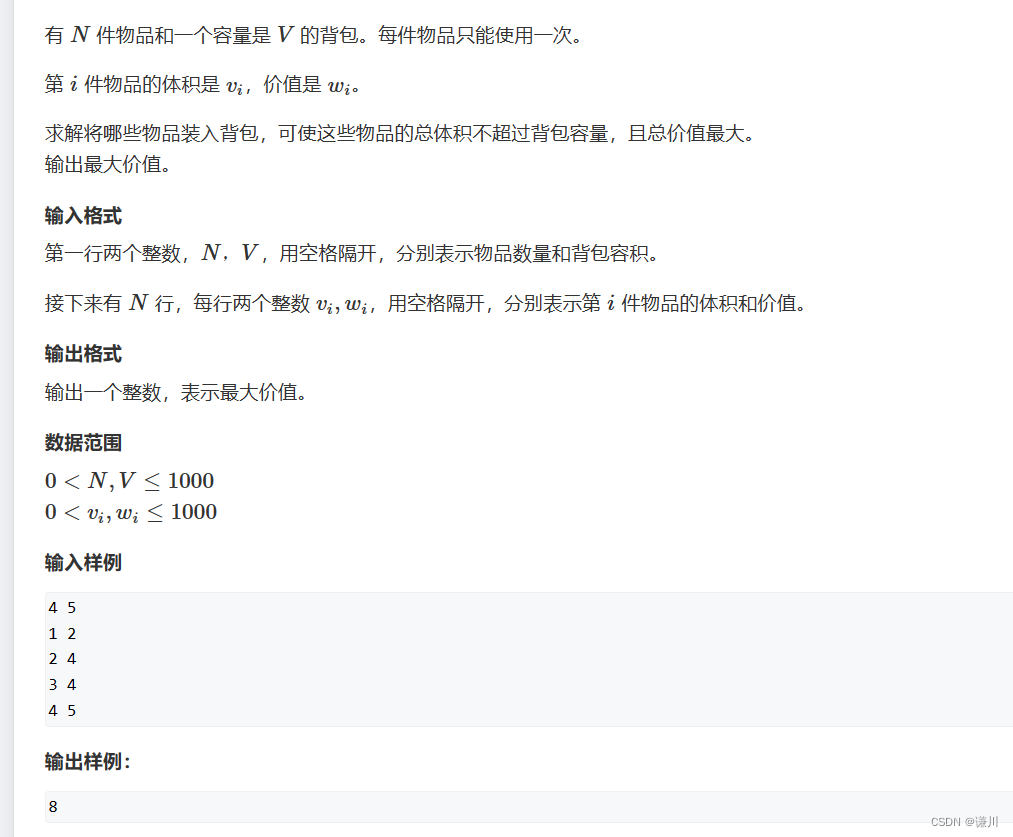
思路 dp
用f[i][j]来表示当体积为j时 考虑前i件物品可以获得的 最大值
记住f[i][j]本身是个价“价值”
考虑两种状态 是否将第i件物品放入背包里面
将背包的体积从小到大递增来进行考虑
首先 考虑条件 如果当前增加的体积放不下下一件物品
则该体积 可以获得的最大值可以直接继承上一个f[i-1][j]
如果可以放下 则比较 放入与不放入谁获得的值较大
即 f[i-1][j]与f[i-1][j-v[i]]+w[i]比较
//-v[i]是为了减去放入后的背包体积
加w[i]是为了加上放入后获得的价值
每一次存下的 都是基于考虑到当前物品 的最优选择
比方说 前面已经进行了i件物品的选择
获得了一个基于i件物品的最大值
这时候 第i+1件物品突然出现 体积为1,价值1000000;
那么当背包体积只有1时的最大值会立刻被更新成100000;
此时仍然是最优选择
代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1010;
int f[N][N];
int w[N],v[N];
int n,m;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>v[i]>>w[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(j<v[i]){
f[i][j]=f[i-1][j];
}else{
f[i][j]=max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
}
}
}
cout<<f[n][m];
return 0;
}
优化思路
二维到一维
我们发现 考虑第i件物品时的最大值来自前面一层i-1件物品的最大值
也就是说 所有的当前层 都只来自上一层的最大值
而上上层已经不重要了
因此有没有可能直接删掉层数记录
观察发现f[i][]是从f[i-1][]这一层更新出来的
此时我们直接删除i
只使用j
观察式子f[j-v[i]]+w[i]
也就是说 如果我们逆序更新的话 需要使用和比较的数是j-v[i]
这个数是绝对小于j的 如果将j从m往0更新
保证了更新时只有大于等于j的数被覆盖掉了
而我们需要用的 j-v[i]则被保留下来
举例
如果我们逆序更新的话
假设 原来 f[j](1-5)是
1 2 5 7 9
然后我们逆序更新
for(int i=0;i<n;i++){
for(int j=m;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
假设 此时j=5,v[i]=2, f[j-v[i]]+w[i]=11那么
我们和上一个f[3]比较 比较完了以后将上一个f[5]覆盖掉
此时f[j](1-5)的情况为
1 2 5 7 11
然后当j=4;
v[i]=1;
f[j-v[i]]+w[i]=9;
即我们需要用的是f[3]
此时f[3]并没有被污染
执行以后
f[j](1-5)的情况为
1 2 5 9 11
以此类推我们的目的达到了
代码
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int f[N];
int w[N],v[N];
int j[N];
int n,m;
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
//int x,y;
cin>>v[i]>>w[i];
//v[i]=x;
//w[i]=y;
}
for(int i=0;i<n;i++){
for(int j=m;j>=v[i];j--){
f[j]=max(f[j],f[j-v[i]]+w[i]);
}
}
cout<<f[m];
return 0;