知识来源:https://www.hello-algo.com/chapter_heap/heap/#4
文章目录
- 2.5 堆
- 2.5.1 堆(优先队列
- 2.5.1.1 堆的常用操作
- 2.5.2 堆的存储与表示
- 2.5.2.1 访问堆顶元素
- 2.5.2.2 入堆
- 时间复杂度
- 2.5.2.3 堆顶元素出堆
- 时间复杂度
- 2.5.3 堆的常见应用
- 2.5.4 建堆问题
- 2.5.4.1 使用入堆操作实现(从底至顶)
- 2.5.4.2 通过遍历堆化实现
- 2.5.4.3 复杂度分析
- 2.5.5 Top-K问题
- 2.5.5.1 遍历选择
- 2.5.5.2 排序
- 2.5.5.3 堆实现
- 时间复杂度分析
- 2.5.6 **代码练习**
- 2.5.6.1 使用数组实现一个堆
- 问题记录 (这部分的代码存在异常,不做参考
- 解读官方的下堆逻辑
- **完整代码**
- 2.5.6.2 使用堆,解决Top-K问题
2.5 堆
2.5.1 堆(优先队列
「堆 heap」是一种满足特定条件的完全二叉树,主要可分为两种类型,
- 「小顶堆 min heap」:任意节点的值 ≤ 其子节点的值。
- 「大顶堆 max heap」:任意节点的值 ≥ 其子节点的值。
需要指出的是,**许多编程语言提供的是「优先队列 priority queue」,**这是一种抽象的数据结构,定义为具有优先级排序的队列。
实际上,堆通常用于实现优先队列,大顶堆相当于元素按从大到小的顺序出队的优先队列。从使用角度来看,我们可以将“优先队列”和“堆”看作等价的数据结构

堆作为完全二叉树的一个特例,具有以下特性。
- 最底层节点靠左填充,其他层的节点都被填满。
- 我们将二叉树的根节点称为“堆顶”,将底层最靠右的节点称为“堆底”。
- 对于大顶堆(小顶堆),堆顶元素(根节点)的值是最大(最小)的。
2.5.1.1 堆的常用操作
Java中对象的实现类为PriorityQueue
/** * 创建一个具有指定初始容量的 PriorityQueue,该队列根据指定的比较器对其元素进行排序。 */ public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) { // Note: 实际上并不需要至少一个的限制,但对 1.5 兼容性的限制会继续存在 if (initialCapacity < 1) throw new IllegalArgumentException(); this.queue = new Object[initialCapacity]; this.comparator = comparator; }
- 可以指定比较器,来区分是大顶堆或者小顶堆
堆的操作效率
| 方法名 | 描述 | 时间复杂度 |
|---|---|---|
push/offer | 元素入堆 | O(logn) |
pop/poll | 堆顶元素出堆 | O(logn) |
peek | 访问堆顶元素(对于大 / 小顶堆分别为最大 / 小值) | O(1) |
size() | 获取堆的元素数量 | O(1) |
isEmpty() | 判断堆是否为空 |
在Java中,堆使用优先队列PriorityQueue来应用:初始化大顶堆(使用 lambda 表达式修改 Comparator 即可)
/* 初始化堆 */
// 初始化小顶堆
Queue<Integer> minHeap = new PriorityQueue<>();
// 初始化大顶堆(使用 lambda 表达式修改 Comparator 即可)
Queue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);
/* 元素入堆 */
maxHeap.offer(1);
maxHeap.offer(3);
maxHeap.offer(2);
maxHeap.offer(5);
maxHeap.offer(4);
/* 获取堆顶元素 */
int peek = maxHeap.peek(); // 5
/* 堆顶元素出堆 */
// 出堆元素会形成一个从大到小的序列
peek = maxHeap.poll(); // 5
peek = maxHeap.poll(); // 4
peek = maxHeap.poll(); // 3
peek = maxHeap.poll(); // 2
peek = maxHeap.poll(); // 1
/* 获取堆大小 */
int size = maxHeap.size();
/* 判断堆是否为空 */
boolean isEmpty = maxHeap.isEmpty();
/* 输入列表并建堆 */
minHeap = new PriorityQueue<>(Arrays.asList(1, 3, 2, 5, 4));
2.5.2 堆的存储与表示
“二叉树”章节讲过,完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树,因此我们将采用数组来存储堆。
- 当使用数组表示二叉树时,元素代表节点值,索引代表节点在二叉树中的位置。
- 查询节点则可以使用公式快速获取(节点指针通过索引映射公式来实现。
- 给定索引 i ,其左子节点的索引为
2i+1,右子节点的索引为2i+2,父节点的索引为(i−1)/2(向下整除)。 - 当索引越界时,表示空节点或节点不存在。
- 给定索引 i ,其左子节点的索引为
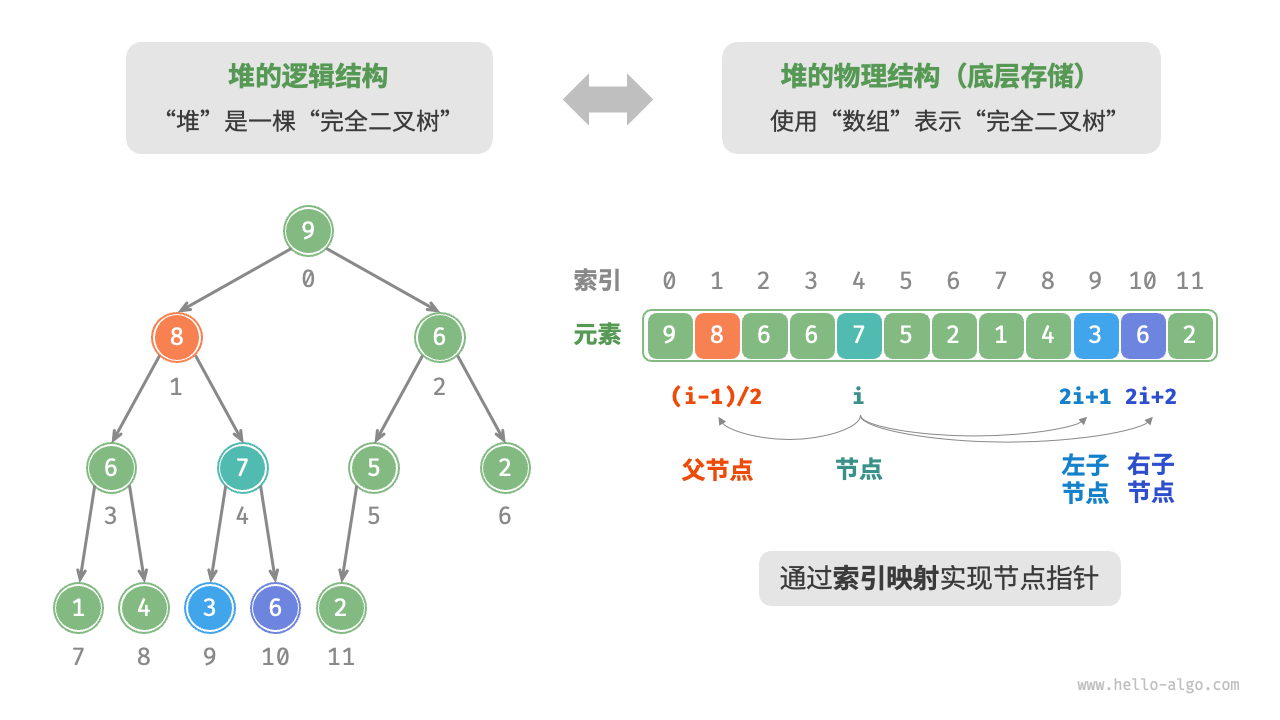
一些对应的操作实现如下
2.5.2.1 访问堆顶元素
堆顶元素就是二叉树的根节点,访问队列的首个元素即可
2.5.2.2 入堆
给定元素 val ,我们首先将其添加到堆底。
添加之后,由于 val 可能大于堆中其他元素,堆的成立条件可能已被破坏,因此需要修复从插入节点到根节点的路径上的各个节点,这个操作被称为「堆化 heapify」。
执行的思路如下:
-
先将节点入堆至堆底;
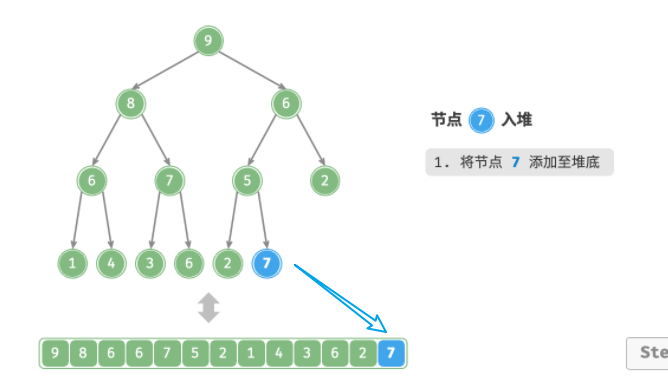
-
比较该节点与父节点的值,如何插入值更大则进行交换

-
继续执行此操作,从堆底修复到堆顶的各个节点
-
直到越过根节点 ,或者遇到无需交换的结点为止
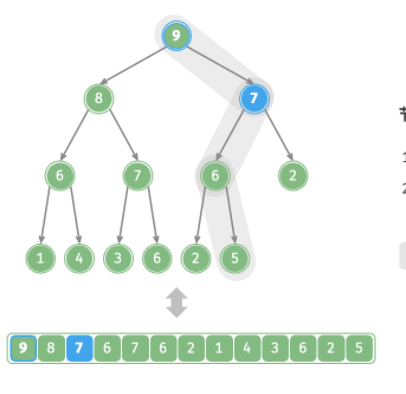
时间复杂度
设节点总数为 n ,则树的高度为 O(logn) 。由此可知,堆化操作的循环轮数最多为 O(logn) ,元素入堆操作的时间复杂度为 O(logn) 。
2.5.2.3 堆顶元素出堆
堆顶元素是二叉树的根节点,即列表首元素。前面已知数组表示下堆顶元素对应索引的第0位
如果直接删除首元素,那么整个堆都会失去含义。为了减少后续堆化的难度,可以将对堆顶元素和堆底元素进行交换后,再进行重新堆化
出堆的思路如下:
-
交换堆顶元素与堆底元素(交换根节点与最右叶节点)。
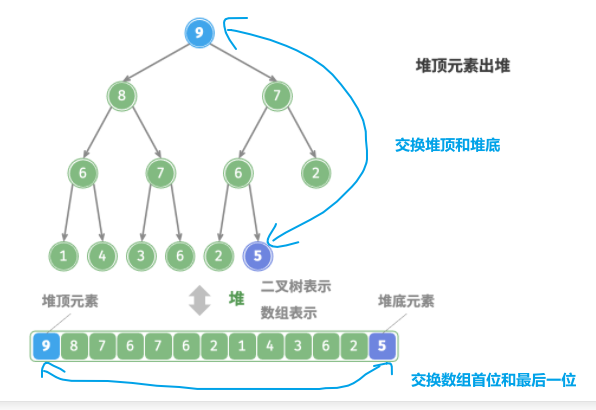
-
交换完成后,将堆底从列表中删除(相当于删除堆顶元素)
-
从根节点开始,从顶至底执行堆化(区分于入堆时的从底到顶的堆化 “从顶至底堆化”的操作方向与“从底至顶堆化”相反)
-
根节点的值与其两个子节点的值进行比较,将最大的子节点与根节点交换
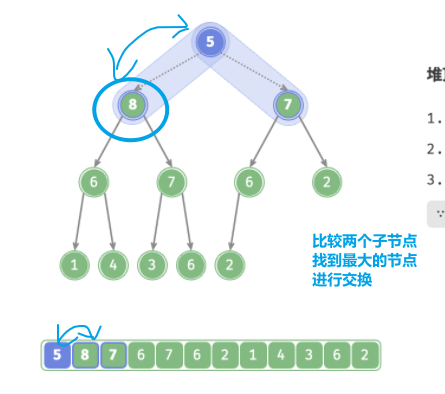
-
循环执行此操作,直到越过叶节点或遇到无须交换的节点时结束
-
时间复杂度
与元素入堆操作相似,堆顶元素出堆操作的时间复杂度也为 O(logn) 。
2.5.3 堆的常见应用
-
优先队列:堆通常作为实现优先队列的首选数据结构(在JAVA中直接等价),其入队和出队操作的时间复杂度均为 O(logn) ,而建队操作为 O(n) ,这些操作都非常高效。
-
堆排序:给定一组数据,我们可以用它们建立一个堆,然后不断地执行元素出堆操作,从而得到有序数据。
-
获取最大的 k 个元素:这是一个经典的算法问题,同时也是一种典型应用,例如选择热度前 10 的新闻作为微博热搜,选取销量前 10 的商品等。
2.5.4 建堆问题
2.5.4.1 使用入堆操作实现(从底至顶)
我们首先创建一个空堆,然后遍历列表,依次对每个元素执行“入堆操作”,即先将元素添加至堆的尾部,再对该元素执行“从底至顶”堆化。
- 每当一个元素入堆,堆的长度就加一。
- 由于节点是从顶到底依次被添加进二叉树的,因此堆是“自上而下”构建的。
设元素数量为 n ,每个元素的入堆操作使用 O(logn) 时间,因此该建堆方法的时间复杂度为 O(nlogn) 。
2.5.4.2 通过遍历堆化实现
实际上,我们可以实现一种更为高效的建堆方法,共分为两步。
- 将列表所有元素原封不动地添加到堆中,此时堆的性质尚未得到满足。
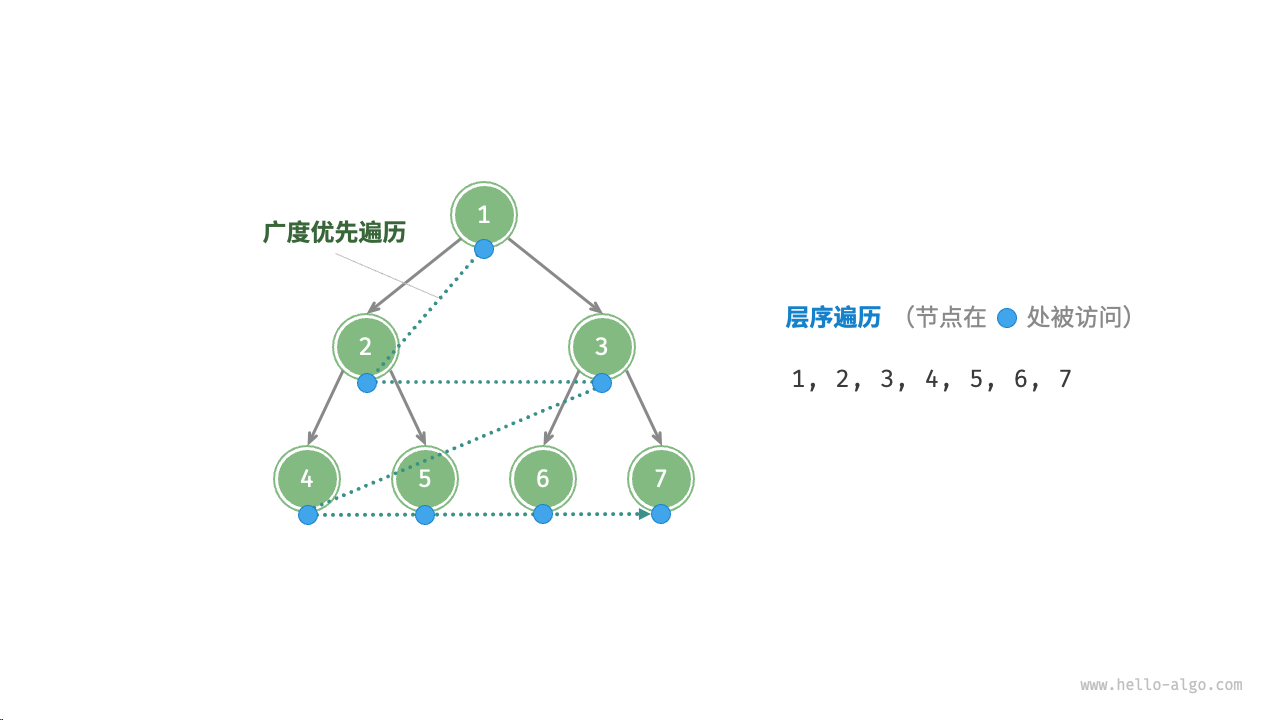
- 倒序遍历堆(层序遍历的倒序),依次对每个非叶节点执行“从顶至底堆化”。
Tips:层序遍历二叉树顺序如下:
值得说明的是,由于叶节点没有子节点,因此它们天然就是合法的子堆,无须堆化。
2.5.4.3 复杂度分析
理论上,自下而上的堆化相比自上而下的堆化可以少堆化一个n的时间复杂度,实际上的计算更加复杂,具体可以看hello算法里给出的推导流程——复杂度分析
引用它的结果可知:
进一步,高度为 h 的完美二叉树的节点数量为 n=2h+1−1 ,易得复杂度为 O(2h)=O(n) 。以上推算表明,输入列表并建堆的时间复杂度为 O(n) ,非常高效。
所以建堆操作也是首选“从顶至底的,自下而上”的遍历建堆实现
代码实现
2.5.5 Top-K问题
Question:
给定一个长度为 n 的无序数组
nums,请返回数组中最大的 k 个元素。
先介绍两种思路比较直接的解法(偏暴力的解法),再介绍效率更高的堆解法。
2.5.5.1 遍历选择
进行 k 轮遍历,分别在每轮中提取第 1、2、…、k 大的元素,时间复杂度为 O(nk) 。
- 此方法只适用于 k≪n 的情况,因为当 k 与 n 比较接近时,其时间复杂度趋向于 O(n2) ,非常耗时。
Tip:
当 k=n 时,我们可以得到完整的有序序列,此时等价于“选择排序”算法。
2.5.5.2 排序
将数组排序后,取出最右边的k个元素。时间复杂度为 O(nlogn) 。
- 显然,该方法“超额”完成任务了,因为我们只需找出最大的 k 个元素即可,而不需要排序其他元素。
2.5.5.3 堆实现
直接给出思路如下:
-
使用第一个元素,初始化一个小顶堆(顶元素最小
-
将数组的第k个元素依次入堆(比如k=3
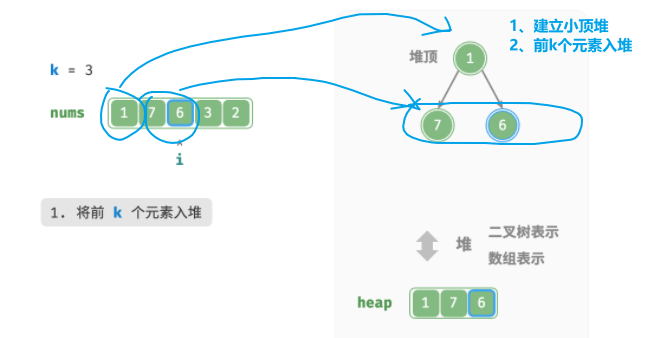
-
从第 k+1 个元素开始,若当前元素大于堆顶元素,则将堆顶元素出堆,并将当前元素入堆。(保证堆的size不变为3)
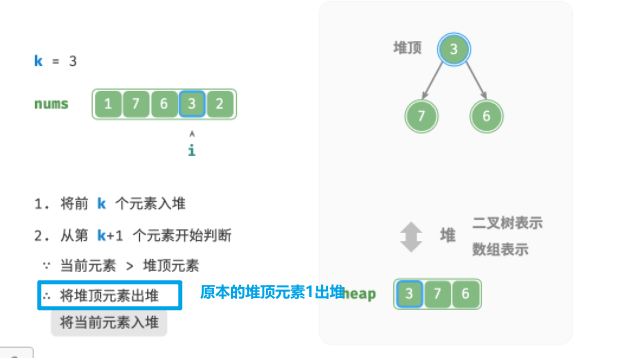

-
遍历完成后,堆中保存的就是最大的 k 个元素。
时间复杂度分析
- 总共执行了 n 轮入堆和出堆,堆的最大长度为 k ,因此时间复杂度为 O(nlogk) 。
- 该方法的效率很高,当 k 较小时,时间复杂度趋向 O(n) ;
- 当 k 较大时,时间复杂度不会超过 O(nlogn)
- 该方法适用于动态数据流的使用场景。在不断加入数据时,我们可以持续维护堆内的元素,从而实现最大的 k 个元素的动态更新。
2.5.6 代码练习
2.5.6.1 使用数组实现一个堆
提供一个堆方法,输入int[]数组返回一个堆,要求能指定堆大小,且能支持上堆入堆和下堆入堆;
问题记录 (这部分的代码存在异常,不做参考
-
当我尝试连续出堆会导致元素丢失问题(数值更大的元素会丢失)
-
比如已堆化数组
[5, 10, 8, 11, 15],预期出堆应该是带排序的[5,8,10,11,15],运行的结果为[5, 10, 11, 8, 8] -
出错的代码如下:
public int poll() { if(size() == 0){ throw new IndexOutOfBoundsException(); } // 交换堆顶元素与堆底元素; 交换完成后,将堆底从列表中删除 int res = peek(); swap(0, size() - 1); // 从根节点开始,从顶至底执行堆化 for (int index = 0; index < size; ) { int temp = arr[index]; int leftNode = this.left(index); int rightNode = this.right(index); // 如果比左子节点大,则进行交换 if (leftNode < size && temp > arr[leftNode]) { swap(index, leftNode); index = leftNode; } // 如果比右子节点大,则进行交换 else if (rightNode < size && temp > arr[rightNode]) { swap(index, rightNode); index = rightNode; } else { break; } } size--; return res; } -
经过排查,发现是在堆顶元素出堆后、堆化的过程出了问题。节点10出堆后,堆中仍然有该元素。

-
问题解决:将
size--的操作提高到堆化之前,防止堆化循环到已经出堆的元素,又重新进入堆中。
-
-
当我尝试添加新元素入堆时,会得到异常的问题。
-
比如
[7, 10, 8],加入元素5,会变成[8,5,7,10]堆化失效 -
分析原因:
- 同样是size的控制问题,再算法实现代码里,对于size的加减应该更前置,避免无谓的错误
- 交换元素问题。易错点,其实整合成方法会更稳定
-
代码修改后
/** * 上堆 * * @param i 开始上堆的下标 */ private void shifUp(int i) { while (true) { // 如果父节点等于自身则结束循环 if (parent(i) == i) { break; } // 如果父节点 > 当前节点,则交换位置! if (arr[parent(i)] > arr[i]) { swap(parent(i), i); } i = parent(i); } }
-
-
再解决了上堆问题后,导致原本的顶堆出堆顺序异常,根据问题2得出的经验,我进一步重写了下堆的方法,思路如下:
- 取出左、右节点
- 选择两个节点中较小的一个节点
- 如果超过数组范围,说明该节点为叶节点,已下堆完成
private void shifDown(int i) { while (true){ int left = left(i); int right = right(i); // 如果左右节点中有一个不存在则结束下堆 if (left >= size() || right >= size()){ break; } // 选择一个小的节点,进行小环 int tar = arr[left] < arr[right] ? left : right; swap(tar , i); i = tar ; } } -
在问题3解决方案上,进一步考虑,有没有一种可能,一个节点刚好有左节点但没有右节点呢?创建一个长度为4的堆,测试如下
上堆添加10,堆节点添加成功:{堆=[10] , size=1} 上堆添加7,堆节点添加成功: {堆=[7, 10] , size=2} 上堆添加8,堆节点添加成功: {堆=[7, 10, 8] , size=3} 上堆添加5,堆节点添加成功: {堆=[5, 7, 8, 10] , size=4} 下堆添加15,堆节点添加成功:{堆=[7, 15, 8, 10] , size=4} 下堆添加11,堆节点添加成功:{堆=[8, 15, 11, 10] , size=4}发现问题:当插入数值15时,堆就被破坏了。说明上述的下堆方法不够完善。
应该分情况讨论:
- 左右节点都存在,当前节点>左、右节点,交换较小的一个节点
- 左右节点都存在,当前节点>其中一个节点,交换该节点.
- 左右节点都存在,当前节点<左、右节点,已经到合适的位置了,结束
- 只有左节点存在,且左节点小于当前节点,交换该节点
- 只有左节点,单左节点大于等于当前节点,不操作,并且结束
- 左右节点都不存在,结束·
。。。。。。。。。。。。。。。。。
解读官方的下堆逻辑
脑壳疼,直接看官方给出的代码吧。
/* 从节点 i 开始,从顶至底堆化 */
void siftDown(int i) {
while (true) {
// 判断节点 i, l, r 中值最大的节点,记为 ma
int l = left(i), r = right(i), ma = i;
if (l < size() && maxHeap.get(l) > maxHeap.get(ma))
ma = l;
if (r < size() && maxHeap.get(r) > maxHeap.get(ma))
ma = r;
// 若节点 i 最大或索引 l, r 越界,则无须继续堆化,跳出
if (ma == i)
break;
// 交换两节点
swap(i, ma);
// 循环向下堆化
i = ma;
}
}
神逻辑:
- 假定一个最大的节点下标为:max
- 先比较左节点的数值,如果左节点数值大,则将max = left
- 再比较右节点
- 判断,如果max的值没变,说明已经到了合适的位置,break
- 交换节点,向下循环
完整代码
小顶堆例子,实现入堆、堆顶出堆;
/**
* @Author zhuhuacong
* @Date: 2024/03/05/ 17:07
* @description 小顶堆
*/
public class MinHeap {
private final int[] nums;
private int size = 0;
private final int capacity;
public MinHeap(int capacity) {
nums = new int[capacity];
this.capacity = capacity;
}
public int peek() {
return nums[0];
}
/**
* 堆顶出堆(最小的数值出堆
*
* @return int
*/
public int poll(){
if (size <= 0){
throw new IndexOutOfBoundsException();
}
int res = peek();
// 交换头尾元素,然后重新入堆
swap(0 , size -1);
size--;
shiftDown(0);
System.out.println("堆顶元素【"+res+"】出堆。堆变化为:"+this);
return res;
}
/**
* 入堆
*
* @param num 要添加的数值
*/
public void add(int num){
// 当堆未被填满时,添加元素到尾部,使用上堆进行堆化
if (size < capacity){
nums[size] = num;
size++;
shiftUp(size -1);
System.out.println("上堆添加"+num+",堆节点添加成功:" + this);
}
// 当堆填满后,如果数值大于堆顶,则互换元素后入堆,使用下堆进行堆化
else if (num > nums[0]){
nums[0] = num;
shiftDown(0);
System.out.println("下堆添加"+num+",堆节点添加成功:" + this);
} else {
System.out.println("没有变化");
}
}
@Override
public String toString() {
StringBuilder sb = new StringBuilder();
for (int i = 0; i < size; i++) {
sb.append(nums[i]).append(i == size - 1 ? "" : ", ");
}
return "{堆=[" + sb +
"]\t, size=" + size +
'}';
}
/**
* 上堆
*
* @param i 下标
*/
void shiftUp(int i){
while (true){
int parent = parent(i);
if (parent != i || nums[parent] < nums[i]){
swap(parent , i);
i = parent;
} else {
break;
}
}
}
/**
* 下堆
*
* @param i 下标
*/
void shiftDown(int i){
while (true){
int l = left(i);
int r = right(i);
int max = i;
// 核心思路,找出左、右、当前节点中数值最大的节点,如果最大的节点是当前节点,说明满足小顶堆的条件,下堆完成
if (l < size && nums[l] < nums[i]){
max = l;
}
if (r < size && nums[r] < nums[max]){
max = r;
}
if (max == i){
break;
}
swap(max , i);
i = max;
}
}
// 左节点
int left(int i) {
return 2 * i + 1;
}
// 右节点
int right(int i) {
return 2 * (i + 1);
}
// 父节点
int parent(int i) {
return (i - 1) / 2;
}
// 交换
void swap(int a, int b) {
if (a < size && b < size) {
int tem = nums[a];
nums[a] = nums[b];
nums[b] = tem;
} else {
System.out.println("无法转换!");
}
}
}
2.5.6.2 使用堆,解决Top-K问题
力扣地址:https://leetcode.cn/problems/xx4gT2/description/
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
public int findKthLargest(int[] nums, int k) {
Queue<Integer> heap = new PriorityQueue<>();
for (int i = 0; i < k; i++) {
heap.add(nums[i]);
}
for (int j = k; j < nums.length ; j++){
if (heap.peek() < nums[j]){
heap.poll();
heap.add(nums[j]);
}
}
return heap.peek();
}
使用java的类库编写速度快,但是效率还没到最快。如果使用自己写的小顶堆方法呢?
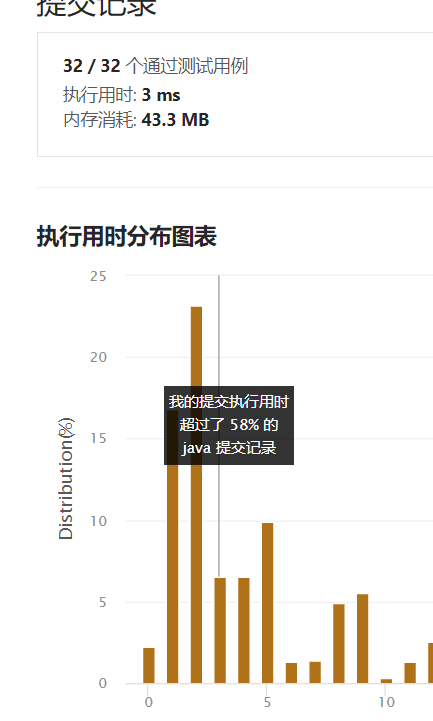
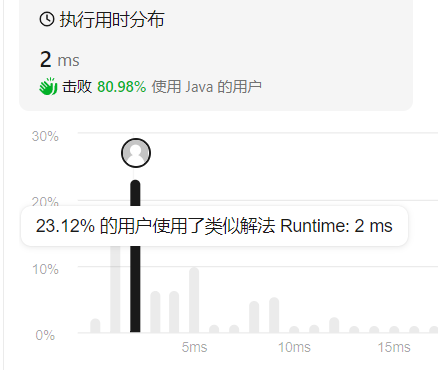
使用以下解法后,效率提高:
class Solution {
public int findKthLargest(int[] nums, int k) {
MinHeap heap = new MinHeap(k);
for(int num : nums){
heap.add(num);
}
return heap.peek();
}
}
class MinHeap {
private final int[] nums;
private int size = 0;
private final int capacity;
public MinHeap(int capacity) {
nums = new int[capacity];
this.capacity = capacity;
}
public int peek() {
return nums[0];
}
/**
* 顶堆出堆(最小的数值出堆
*
* @return int
*/
public int poll() {
if (size <= 0) {
throw new IndexOutOfBoundsException();
}
int res = peek();
// 交换头尾元素,然后重新入堆
swap(0, size - 1);
size--;
shiftDown(0);
return res;
}
/**
* 入堆
*
* @param num 要添加的数值
*/
public void add(int num) {
// 当堆未被填满时,添加元素到尾部,使用上堆进行堆化
if (size < capacity) {
nums[size] = num;
size++;
shiftUp(size - 1);
}
// 当堆填满后,如果数值大于堆顶,则互换元素后入堆,使用下堆进行堆化
else if (num > nums[0]) {
nums[0] = num;
shiftDown(0);
}
}
/**
* 上堆
*
* @param i 下标
*/
void shiftUp(int i) {
while (true) {
int parent = parent(i);
if (parent != i && nums[parent] > nums[i]) {
swap(parent, i);
i = parent;
} else {
break;
}
}
}
/**
* 下堆
*
* @param i 下标
*/
void shiftDown(int i) {
while (true) {
int l = left(i);
int r = right(i);
int max = i;
// 核心思路,找出左、右、当前节点中数值最大的节点,如果最大的节点是当前节点,说明满足小顶堆的条件,下堆完成
if (l < size && nums[l] < nums[i]) {
max = l;
}
if (r < size && nums[r] < nums[max]) {
max = r;
}
if (max == i) {
break;
}
swap(max, i);
i = max;
}
}
// 左节点
int left(int i) {
return 2 * i + 1;
}
// 右节点
int right(int i) {
return 2 * (i + 1);
}
// 父节点
int parent(int i) {
return (i - 1) / 2;
}
// 交换
void swap(int a, int b) {
if (a < size && b < size) {
int tem = nums[a];
nums[a] = nums[b];
nums[b] = tem;
}
}
}

![[项目设计] 从零实现的高并发内存池(五)](https://img-blog.csdnimg.cn/c446ebae288e480d84f5d14d494c88bb.gif)