目录
一、什么是并查集
二、并查集的原理
三、并查集的作用
四、并查集的代码实现
一、什么是并查集
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个 单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一 个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
二、并查集的原理
下面来看一个例子:某算法竞赛今年全国决赛总共有10人,4人来自西安,3人来自安徽,3人来自上海,10个人均来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
再用一个数组用来存储该小集体,数组下标表示学生的编号,数组中存储的数字我们先将其全部设为-1(为什么是-1下文会具体讲解):

竞赛时,每个地方的学生自发组织成小分队一起合作,于是:西安学生小分队s1={0,6,7,8},安徽学生小分队s2={1,4,9},上海学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。假设右三个群主0,1,2担任队长,负责组员的管理
这样子这10个学生就分成了三个组,我们用树的方式来表示一下:
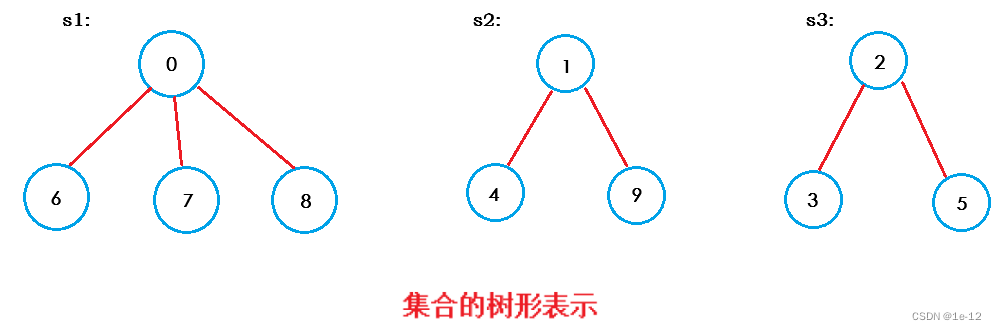
下面我们使用双亲表示法,在之前建立的数组中进行三个小组的划分:
划分方法为:如果元素下标所表示的学生是组长不进行任何操作;如果下标所表示的学生是组员就将其下标的所对应的元素值加到所属组长的元素值上,再将自己的元素值改为组长所在元素下标:
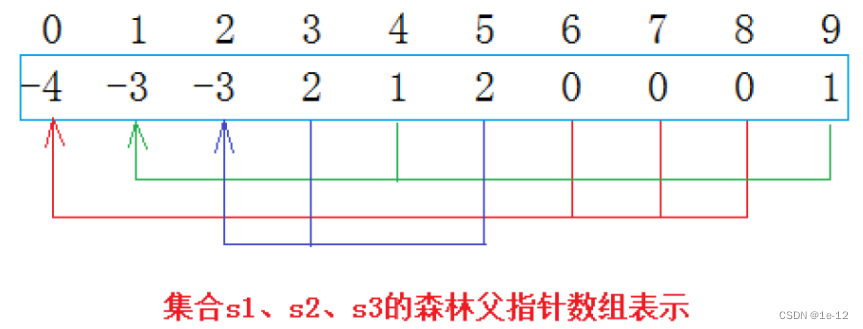
这样处理过后我们可以发现:数组中存储的数字如果为负数,意味着该值所在的元素下标对应的学生是组长(树的根),其绝对值也代表该小集体中具有成员的个数(树的节点数);如果为不为负数,意味着该值所在的元素下标对应的学生是组员(树的叶子),其值也代表组长所在下标(指向自己的根)
按照上面的方法我们就可以使用数组来实现多棵树(森林)的表示了(和堆有点相似)
在比赛结束后,西安小分队中8号同学与安徽小分队4号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后成为了以0号同学为主导的一个小圈子:
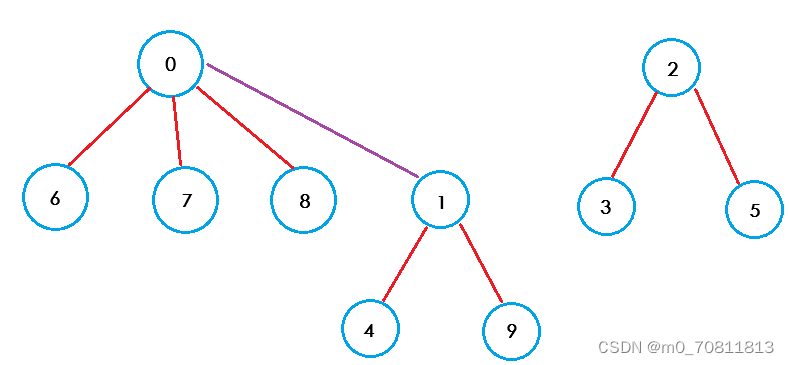
那树的形状发生了变化,数组对应的数据也会进行变化:
在数组中,一棵树要和另一棵树进行融合,先要找到要融合数据所对应的下标:例子里是4号同学,对应4号下标
再判断下标所在元素的数值,数值为正就继续找数值所对应的下标元素,一直找到数值为负的下标为止(找到要融合数据所在的根):先找到4号下标对应的数据是1,不是负数,那就继续找到1号下标所在的元素,其数值为-3,满足条件
最后将找到的根节点的数值加到另一棵树的根节点的数值上,再将其原本的根节点的数值改为另一棵树的根节点的下标:

现在0集合有7个人,2集合有3个人,总共两个朋友圈。
三、并查集的作用
通过以上例子可知,并查集一般可以解决一下问题:
1. 查找元素属于哪个集合,沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置)
2. 查看两个元素是否属于同一个集合,沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
3. 将两个集合归并成一个集合,将两个集合中的元素合并,将一个集合名称改成另一个集合的名称
4. 集合的个数遍历数组,数组中元素为负数的个数即为集合的个数。
四、并查集的代码实现
#include<iostream>
#include<vector>
using namespace std;
class UnionFindSet
{
public:
UnionFindSet(size_t n)//初始化数据
:_ufs(n,-1)
{}
int FindRoot(int n)//查找元素的根节点
{
int parent = n;
while (_ufs[parent] >= 0)
{
parent = _ufs[parent];
}
return parent;
}
void Union(int x, int y)//合并两个元素所在树
{
int root1 = FindRoot(x);
int root2 = FindRoot(y);
if (root1 == root2)//元素所在树都一样就没必要合并了
return;
if (root1 > root2)//取较小值的根节点来合并
swap(root1, root2);
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
bool InSet(int x, int y)//判断两个元素是否在同一棵树
{
return FindRoot(x) == FindRoot(y);
}
size_t SetSize()//返回并查集中树的个数
{
size_t size = 0;
for (auto e : _ufs)
{
if (e < 0)
++size;
}
return size;
}
private:
vector<int> _ufs;
};上述的代码实现的只是一个基本的并查集,如果并不想用元素下标来直接表示数据类型,我们可以使用map来建立对应的映射关系